前言
实验目的
- 阅读论文《HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification》,并思考3D卷积和2D卷积的区别;
- 阅读代码:https://gaopursuit.oss-cn-beijing.aliyuncs.com/202010/AIexp/10%20-%20HybridSN_GRSL2020.mhtml;
- 把代码在 Colab 运行,网络部分需要自己完成;
- 训练网络,然后多测试几次,会发现每次分类的结果都不一样,请思考为什么?
- 同时,思考问题,如果想要进一步提升高光谱图像的分类性能,可以如何使用注意力机制?
- 本次博客关键词:高光谱分类(论文中的),注意力机制(自己加的)。
论文地址
论文下载地址1:https://ieeexplore.ieee.org/document/8736016
论文下载地址2:https://pan.baidu.com/s/1dK811oJrGdhUwDSlel9PZA 提取码:55ty
一、论文解读
1、这篇论文说了啥?
首先,介绍一下本论文的主角——高光谱图像(HyperSpectral Image,简称HSI):
- 即包含光谱信息特别长的图像(包含红外线、紫外线等不可见光光谱),比如:普通照片只有三个通道,即RGB——红、绿、蓝。数据类型是一个m ∗ n ∗ 3 m*n*3m∗n∗3的矩阵,而高光谱图像则是M ∗ N ∗ B M*N*BM∗N∗B(B是光谱的层数:3层RGB+其他光谱层…)。
- 高光谱图像是一个立体的三维结构,x、y表示二维平面像素信息坐标轴,第三维是波长信息坐标轴。
之后,对于卷积网络,处理高光谱图像时,会有一些技术问题:
- 2-D-CNN无法处理数据的第三维度——光谱信息(前两维度是图像本身的x轴和y轴)。
- 传统的2D-卷积处理不好这种三维的高光谱图像;
- 若只使用3D-卷积,虽然可以提取第三维——光谱维度的特征,能同时进行空间和空间特征表示,但数据计算量特别大,且对特征的表现能力比较差(因为许多光谱带上的纹理是相似的)
所以,作者:
- 提出HybirdSN模型(全称是Hybrid SpectralNet——我大致翻译为:混合了2D、3D卷积的光谱网络):将空间光谱和光谱的互补信息分别以3D-CNN和2D-CNN层组合到了一起,从而充分利用了光谱和空间特征图,来克服以上缺点。
- HybirdSN模型比3D-CNN模型的计算效率更高。在小的训练数据上也显示出了优越的性能。
2、实现步骤
(1)PCA主成分分析
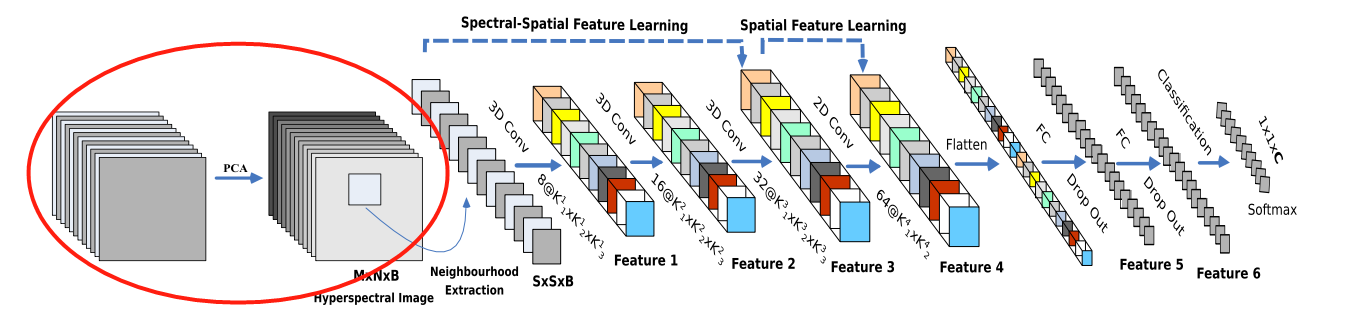
- 首先,对于输入的高光谱图像,进行了主成分分析(PCA),减少了第三维数据的一些光谱波段,只保留了对识别物体重要的空间信息;
- 将数据的输入规范化为M ∗ N ∗ B M*N*BM∗N∗B;
(2)将数据划分为三维小块
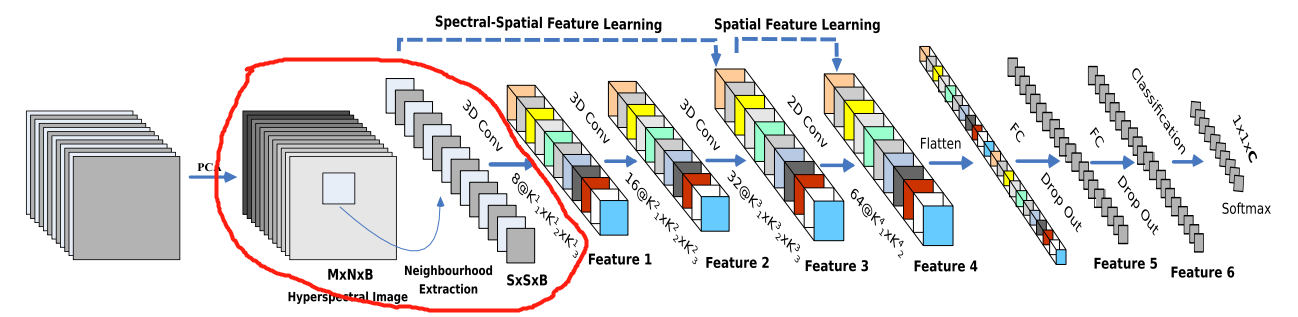
- 随后将数据划分为重叠的三维小块S ∗ S ∗ B S*S*BS∗S∗B(“厚度”不变),小块的label由中心像素的label决定。
(3)三维卷积提取光谱维度特征
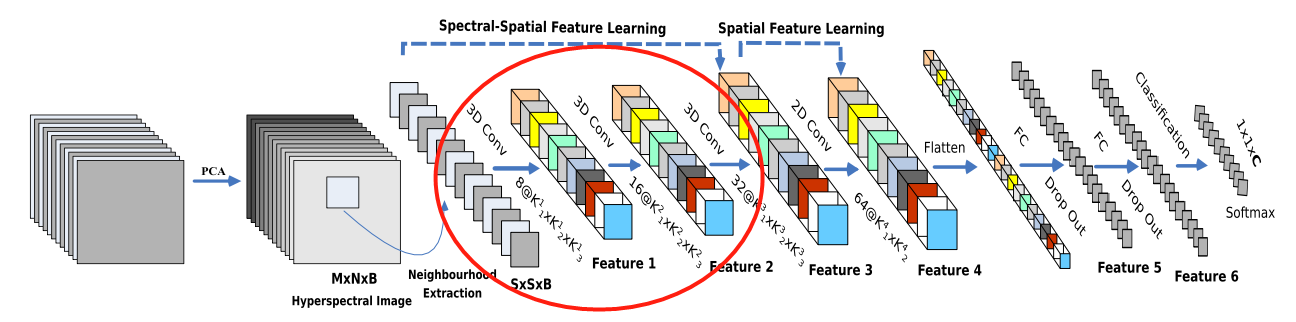
- 之后,使用3D-卷积获取光谱维度和图像间的特征;
- 三次三维卷积中,卷积核的尺寸依次为:
- 8×3×3×7×1(8是他自己设计的卷积核的个数,3 ∗ 3 ∗ 7 3*3*73∗3∗7是一个三维卷积核的大小,1是因为一共只有1组图,所以再乘个1)、
- 16×3×3×5×8、
- 32×3×3×3×16。
- 在三维卷积中,生成第i层第j个feature map在空间位置(x, y,z)的激活值,记为v i , j x , y , z v_{i,j}^{x,y,z}vi,jx,y,z,公式2如下图所示:
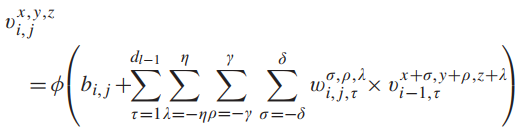
(4)二维卷积卷图像特征
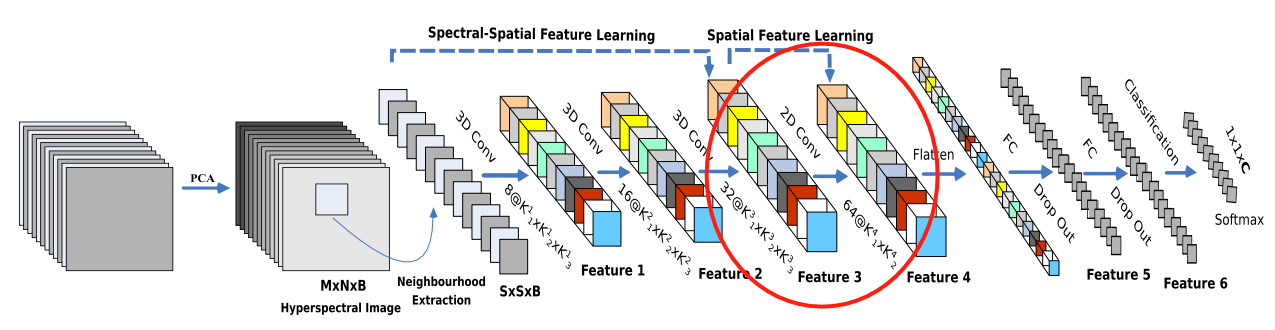
- 使用2D-卷积获取图像本身的特征;
- 二维卷积中,卷积核的尺寸为64×3×3×576(576为二维输入特征图的数量)。
- 在二维卷积中,第i ii层第j jj个feature map在空间位置(x, y)处的值,记为v i , j x , y v_{i,j}^{x,y}vi,jx,y,其生成公式1如下:
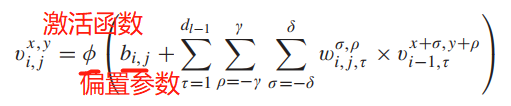
(5)全连接输出
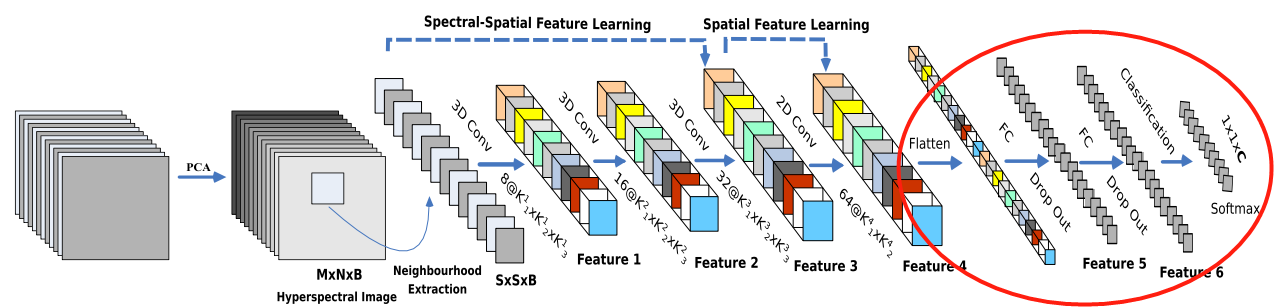
- 接下来是一个 flatten 操作(为了输出给全连接层,所以必须是一条二维数据),变为 18496 维的向量;
- 接下来依次为256,128节点的全连接层,都使用比例为0.4的 Dropout(就是扔掉40%的数据,防止模型过拟合);
- 最后输出为 16 个节点,是分类的种数(之所以是16类,是因为它选取的数据集,本身的标签最多就是16类,参见下面的表格)。
3、数据集来源
实验使用了三个公开的HSI数据集:Indian Pines (IP)、University of Pavia (UP)和Salinas Scene (SA)。
| 数据集 | 图像维数 | 波长范围 | 光谱波段个数 | 地面图像被划分为多少类 |
|---|---|---|---|---|
| Indian Pines (IP) | 145 ∗ 145 145 *145145∗145 | 400 ~ 2500 nm | 224 | 16 |
| University of Pavia (UP) | 610 ∗ 340 610 *340610∗340 | 430~ 860 nm | 103 | 9 |
| Salinas Scene (SA) | 512 ∗ 217 512 * 217512∗217 | 360 ~2500 nm | 224 | 16 |
4、分类效果对比

5、每层的参数及输出
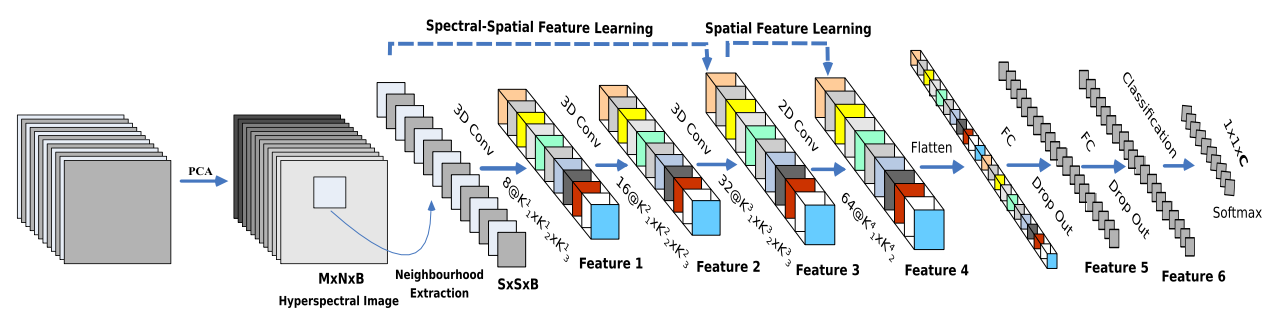
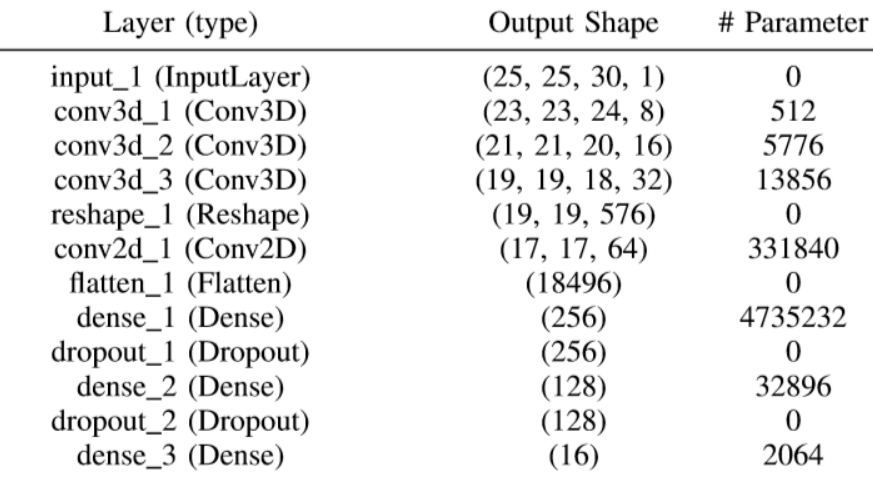
二、工程实现
注意:
- 本次的实验的运行环境为colab,需要科学上网。
1、数据准备+引入基本函数库
首先取得数据——Indian pines(这是论文中引用的三个数据集中的一个)
#数据准备
! wget http://www.ehu.eus/ccwintco/uploads/6/67/Indian_pines_corrected.mat
! wget http://www.ehu.eus/ccwintco/uploads/c/c4/Indian_pines_gt.mat
! pip install spectral
##引入基本函数库
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report, cohen_kappa_score
import spectral
import torch
import torchvision
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
2、定义 HybridSN类
包括:
- 三维卷积部分的定义(细节见 一.2.(3)部分)
- 二维卷积的定义(细节见 一.2.(4)部分)
- flatten 操作(细节见 一.2.(5)部分)
- 全连接层(细节见 一.2.(5)部分)
- 40%的 Dropout(细节见 一.2.(5)部分)
- 最后输出为 16 个节点(细节见一.2.(5)部分)
代码实现:
##定义 HybridSN 类
class_num = 16
class HybridSN(nn.Module):
def __init__(self, num_classes=16):
super(HybridSN, self).__init__()
# conv1:(1, 30, 25, 25), 8个 7x3x3 的卷积核 ==>(8, 24, 23, 23)
self.conv1 = nn.Conv3d(1, 8, (7, 3, 3))
# conv2:(8, 24, 23, 23), 16个 5x3x3 的卷积核 ==>(16, 20, 21, 21)
self.conv2 = nn.Conv3d(8, 16, (5, 3, 3))
# conv3:(16, 20, 21, 21),32个 3x3x3 的卷积核 ==>(32, 18, 19, 19)
self.conv3 = nn.Conv3d(16, 32, (3, 3, 3))
# conv3_2d (576, 19, 19),64个 3x3 的卷积核 ==>((64, 17, 17)
self.conv3_2d = nn.Conv2d(576, 64, (3,3))
# 全连接层(256个节点)
self.dense1 = nn.Linear(18496,256)
# 全连接层(128个节点)
self.dense2 = nn.Linear(256,128)
# 最终输出层(16个节点)
self.out = nn.Linear(128, num_classes)
# Dropout(0.4)
self.drop = nn.Dropout(p=0.4)
######################
#这里是优化的方向(一会还会添加注意力机制)
######################
#软最大化
#self.soft = nn.LogSoftmax(dim=1)
self.soft = nn.Softmax(dim=1)
#加入BN归一化数据
self.bn1=nn.BatchNorm3d(8)
self.bn2=nn.BatchNorm3d(16)
self.bn3=nn.BatchNorm3d(32)
self.bn4=nn.BatchNorm2d(64)
# 激活函数ReLU
self.relu = nn.ReLU()
#####################
#####################
#定义完了各个模块,记得在这里调用执行:
def forward(self, x):
out = self.relu(self.conv1(x))
#out = self.bn1(out)#BN层
out = self.relu(self.conv2(out))
#out = self.bn2(out)#BN层
out = self.relu(self.conv3(out))
#out = self.bn3(out)#BN层
out = out.view(-1, out.shape[1] * out.shape[2], out.shape[3], out.shape[4])# 进行二维卷积,因此把前面的 32*18 reshape 一下,得到 (576, 19, 19)
#out = self.attention(out)#调用注意力机制
out = self.relu(self.conv3_2d(out))
#out = self.bn4(out)#BN层
# flatten 操作,变为 18496 维的向量,
out = out.view(out.size(0), -1)
out = self.dense1(out)
out = self.drop(out)
out = self.dense2(out)
out = self.drop(out)
out = self.out(out)
out = self.soft(out)
return out
3、定义其他操作函数:主成分分析、创建数据集等…
在这一步,我们主要完成:
- 创建数据集 首先对高光谱数据实施PCA降维;
- 创建方便处理的数据格式;
- 随机抽取 10% 数据做为训练集,剩余的做为测试集。
首先,我们定义一些基本函数来完成上述功能的基础部分:
# 对高光谱数据 X 应用 PCA 变换
def applyPCA(X, numComponents):
newX = np.reshape(X, (-1, X.shape[2]))
pca = PCA(n_components=numComponents, whiten=True)
newX = pca.fit_transform(newX)
newX = np.reshape(newX, (X.shape[0], X.shape[1], numComponents))
return newX
# 对单个像素周围提取 patch 时,边缘像素就无法取了,因此,给这部分像素进行 padding 操作
def padWithZeros(X, margin=2):
newX = np.zeros((X.shape[0] + 2 * margin, X.shape[1] + 2* margin, X.shape[2]))
x_offset = margin
y_offset = margin
newX[x_offset:X.shape[0] + x_offset, y_offset:X.shape[1] + y_offset, :] = X
return newX
# 在每个像素周围提取 patch ,然后创建成符合 keras 处理的格式
def createImageCubes(X, y, windowSize=5, removeZeroLabels = True):
# 给 X 做 padding
margin = int((windowSize - 1) / 2)
zeroPaddedX = padWithZeros(X, margin=margin)
# split patches
patchesData = np.zeros((X.shape[0] * X.shape[1], windowSize, windowSize, X.shape[2]))
patchesLabels = np.zeros((X.shape[0] * X.shape[1]))
patchIndex = 0
for r in range(margin, zeroPaddedX.shape[0] - margin):
for c in range(margin, zeroPaddedX.shape[1] - margin):
patch = zeroPaddedX[r - margin:r + margin + 1, c - margin:c + margin + 1]
patchesData[patchIndex, :, :, :] = patch
patchesLabels[patchIndex] = y[r-margin, c-margin]
patchIndex = patchIndex + 1
if removeZeroLabels:
patchesData = patchesData[patchesLabels>0,:,:,:]
patchesLabels = patchesLabels[patchesLabels>0]
patchesLabels -= 1
return patchesData, patchesLabels
def splitTrainTestSet(X, y, testRatio, randomState=345):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=testRatio, random_state=randomState, stratify=y)
return X_train, X_test, y_train, y_test
读取并创建数据集:
# 地物类别
class_num = 16
X = sio.loadmat('Indian_pines_corrected.mat')['indian_pines_corrected']
y = sio.loadmat('Indian_pines_gt.mat')['indian_pines_gt']
# 用于测试样本的比例
test_ratio = 0.90
# 每个像素周围提取 patch 的尺寸
patch_size = 25
# 使用 PCA 降维,得到主成分的数量
pca_components = 30
print('Hyperspectral data shape: ', X.shape)
print('Label shape: ', y.shape)
print('\n... ... PCA tranformation ... ...')
X_pca = applyPCA(X, numComponents=pca_components)
print('Data shape after PCA: ', X_pca.shape)
print('\n... ... create data cubes ... ...')
X_pca, y = createImageCubes(X_pca, y, windowSize=patch_size)
print('Data cube X shape: ', X_pca.shape)
print('Data cube y shape: ', y.shape)
print('\n... ... create train & test data ... ...')
Xtrain, Xtest, ytrain, ytest = splitTrainTestSet(X_pca, y, test_ratio)
print('Xtrain shape: ', Xtrain.shape)
print('Xtest shape: ', Xtest.shape)
# 改变 Xtrain, Ytrain 的形状,以符合 keras 的要求
Xtrain = Xtrain.reshape(-1, patch_size, patch_size, pca_components, 1)
Xtest = Xtest.reshape(-1, patch_size, patch_size, pca_components, 1)
print('before transpose: Xtrain shape: ', Xtrain.shape)
print('before transpose: Xtest shape: ', Xtest.shape)
# 为了适应 pytorch 结构,数据要做 transpose
Xtrain = Xtrain.transpose(0, 4, 3, 1, 2)
Xtest = Xtest.transpose(0, 4, 3, 1, 2)
print('after transpose: Xtrain shape: ', Xtrain.shape)
print('after transpose: Xtest shape: ', Xtest.shape)
""" Training dataset"""
class TrainDS(torch.utils.data.Dataset):
def __init__(self):
self.len = Xtrain.shape[0]
self.x_data = torch.FloatTensor(Xtrain)
self.y_data = torch.LongTensor(ytrain)
def __getitem__(self, index):
# 根据索引返回数据和对应的标签
return self.x_data[index], self.y_data[index]
def __len__(self):
# 返回文件数据的数目
return self.len
""" Testing dataset"""
class TestDS(torch.utils.data.Dataset):
def __init__(self):
self.len = Xtest.shape[0]
self.x_data = torch.FloatTensor(Xtest)
self.y_data = torch.LongTensor(ytest)
def __getitem__(self, index):
# 根据索引返回数据和对应的标签
return self.x_data[index], self.y_data[index]
def __len__(self):
# 返回文件数据的数目
return self.len
# 创建 trainloader 和 testloader
trainset = TrainDS()
testset = TestDS()
train_loader = torch.utils.data.DataLoader(dataset=trainset, batch_size=128, shuffle=True, num_workers=2)
test_loader = torch.utils.data.DataLoader(dataset=testset, batch_size=128, shuffle=False, num_workers=2)
4、训练模型
# 使用GPU训练,可以在菜单 "代码执行工具" -> "更改运行时类型" 里进行设置
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 网络放到GPU上
net = HybridSN().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)#设置学习率
# 计时
import time
time_start=time.time()
# 开始训练
total_loss = 0
for epoch in range(100):
for i, (inputs, labels) in enumerate(train_loader):
inputs = inputs.to(device)
labels = labels.to(device)
# 优化器梯度归零
optimizer.zero_grad()
# 正向传播 + 反向传播 + 优化
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
total_loss += loss.item()
print('[Epoch: %d] [loss avg: %.4f] [current loss: %.4f]' %(epoch + 1, total_loss/(epoch+1), loss.item()))
time_end=time.time()
print('totally cost',time_end-time_start)
print('Finished Training')

5、测试模型
#训练完了,开始模型测试
count = 0
# 模型测试
for inputs, _ in test_loader:
inputs = inputs.to(device)
outputs = net(inputs)
outputs = np.argmax(outputs.detach().cpu().numpy(), axis=1)
if count == 0:
y_pred_test = outputs
count = 1
else:
y_pred_test = np.concatenate( (y_pred_test, outputs) )
# 生成分类报告
classification = class
三、优化和改进
个人感觉,在本代码中只有
- BN层的有无
- 和具体的softMax的方法
可以优化,故做了以下实验:
1、最开始我只是用的softMax函数进行软最大化:
#这里是优化的方向
#软最大化
#self.soft = nn.LogSoftmax(dim=1)
self.soft = nn.Softmax(dim=1)
#加入BN归一化数据
#self.bn1=nn.BatchNorm3d(8)
#self.bn2=nn.BatchNorm3d(16)
#self.bn3=nn.BatchNorm3d(32)
#self.bn4=nn.BatchNorm2d(64)
结果如下

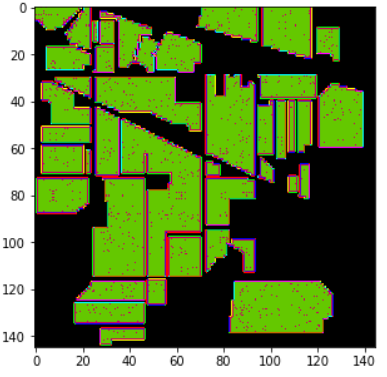
- 平均损失竟然有21,分类效果也很不明显,结果不够令人满意,所以有了接下来的优化:
2、使用LogSoftmax替代softMax
- 一开始我用的softmax函数,即self.soft = nn.Softmax(dim=1);
- 但经过查询其他博客,我发现还有logsoftmax,在使用logsoftmax代替softmax之后,效果显著提升;
- log_softmax能够解决函数overflow和underflow,加快运算速度,提高数据稳定性。
- 具体原理我就不赘述了,参考这里——https://www.zhihu.com/question/358069078
#这里是优化的方向
#软最大化
self.soft = nn.LogSoftmax(dim=1)
#self.soft = nn.Softmax(dim=1)
#加入BN归一化数据
#self.bn1=nn.BatchNorm3d(8)
#self.bn2=nn.BatchNorm3d(16)
#self.bn3=nn.BatchNorm3d(32)
#self.bn4=nn.BatchNorm2d(64)

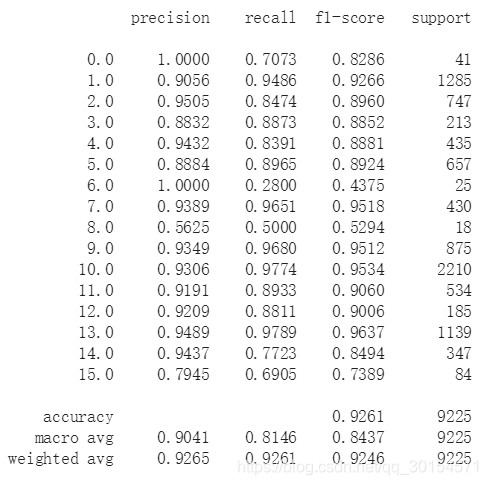
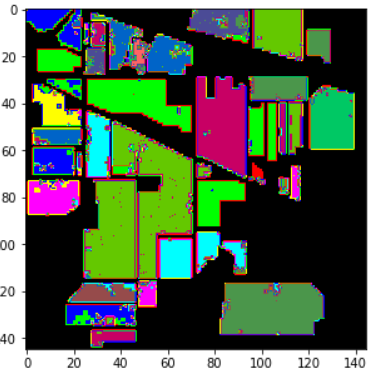
- 准确率为92.6%,视觉效果也还不错,但是还能不能更近一步呢?
3、添加了BN+LogSoftmax
- 由于之前我做过一些用神经网络进行超分辨率重建的实验,在过程中接触了BN这个东西(BatchNorm),得知他很适合做分类任务,所以也拿来写在我的网络里,看看效果。
- 具体什么是BN,我会在后面补充。
#这里是优化的方向
#软最大化
self.soft = nn.LogSoftmax(dim=1)
#self.soft = nn.Softmax(dim=1)
#加入BN归一化数据
self.bn1=nn.BatchNorm3d(8)
self.bn2=nn.BatchNorm3d(16)
self.bn3=nn.BatchNorm3d(32)
self.bn4=nn.BatchNorm2d(64)
def forward(self, x):
out = self.relu(self.conv1(x))
out = self.bn1(out)#BN层
out = self.relu(self.conv2(out))
out = self.bn2(out)#BN层
out = self.relu(self.conv3(out))
out = self.bn3(out)#BN层
# 进行二维卷积,因此把前面的 32*18 reshape 一下,得到 (576, 19, 19)
out = out.view(-1, out.shape[1] * out.shape[2], out.shape[3], out.shape[4])
out = self.relu(self.conv3_2d(out))
out = self.bn4(out)#BN层
# flatten 操作,变为 18496 维的向量,
out = out.view(out.size(0), -1)
out = self.dense1(out)
out = self.drop(out)
out = self.dense2(out)
out = self.drop(out)
out = self.out(out)
out = self.soft(out)
return out
BN+LogSoftmax的结果: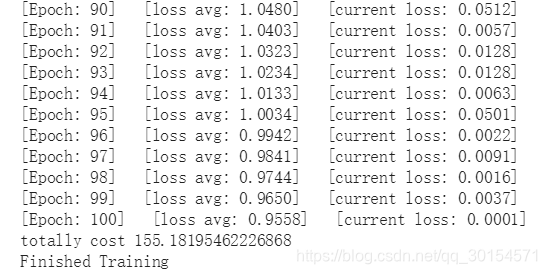
模型的训练准确率又有了一定的提升!!!

测试准确率从92%升到了93.7%,有一定的提升。
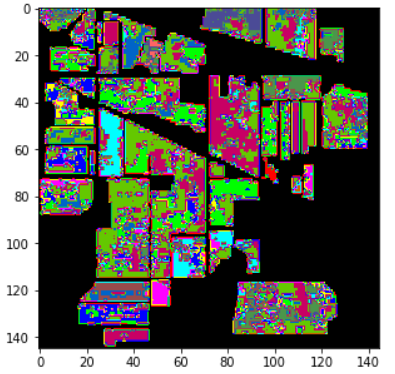
但是这个视觉效果…是实在是不敢恭维…
所以我得出结论:
- 优化效果最明显的还是将softmax函数换为LogSoftMax
- BN对于模型准确率有一定的提升,但是可能是由于其破坏了图像的对比度?最终出来的图片分类视觉效果很差。
补充——什么是Batch Norm:
- 个人感觉,Batch Norm是深度学习中出镜率很高的一项技术,可以使训练更容易、加速收敛、防止模型过拟合。在很多基于CNN的分类任务中,被大量使用(个人理解,BN层很适合分类任务!)。
- BN对图像来说类似于一种对比度的拉伸,其色彩的分布都会被归一化,会破坏了图像原本的对比度信息(所以BN就不适合做超清晰度重建之类的任务)。
- 但是图像分类不需要保留图像的对比度信息,利用图像的结构信息就可以完成分类,所以Batch Norm反而降低了训练难度,甚至一些不明显的结构,在Batch Norm后也会被凸显出来(对比度被拉开了)。
四、思考题
1、2D卷积和3D卷积的区别
2D卷积:
二维卷积大家都很熟悉,就是通常所用到的“普通”卷积,其卷积过程见下图: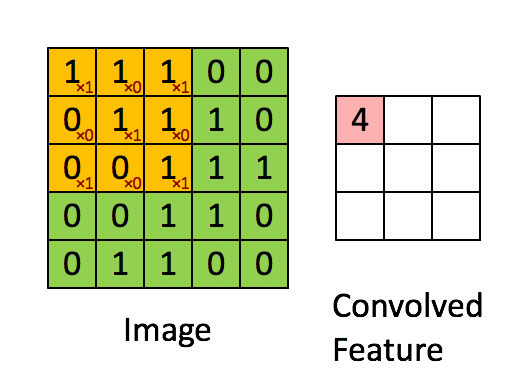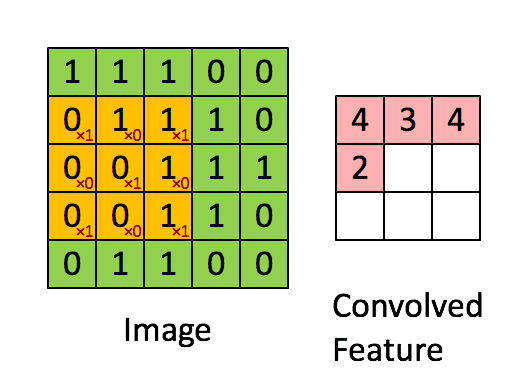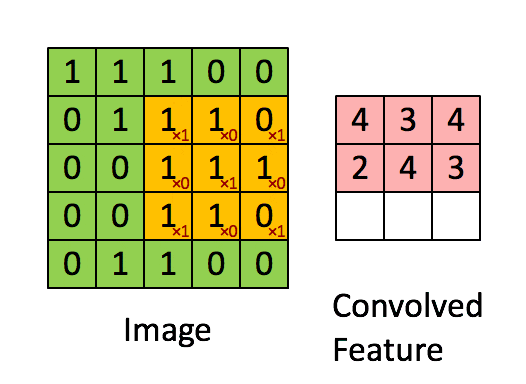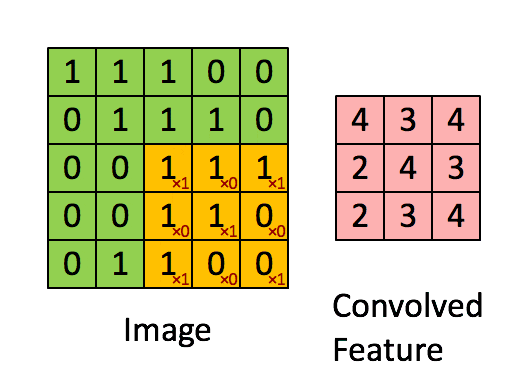
个人理解:
- 在二维卷积中,输入的大图片与二维的卷积核进行卷积,输出的是一张二维的小图片(这个小图片也叫做特征矩阵、特征图…),当然也只能提取二维的平面特征。
- 如果数据类型其本身的特征分布是三维的,那么仅仅用二维卷积提取到的特征就会不全面,都没有完全利用输入数据。
3D卷积:
三维卷积类似于下图(坐标轴的注释与本文无关):
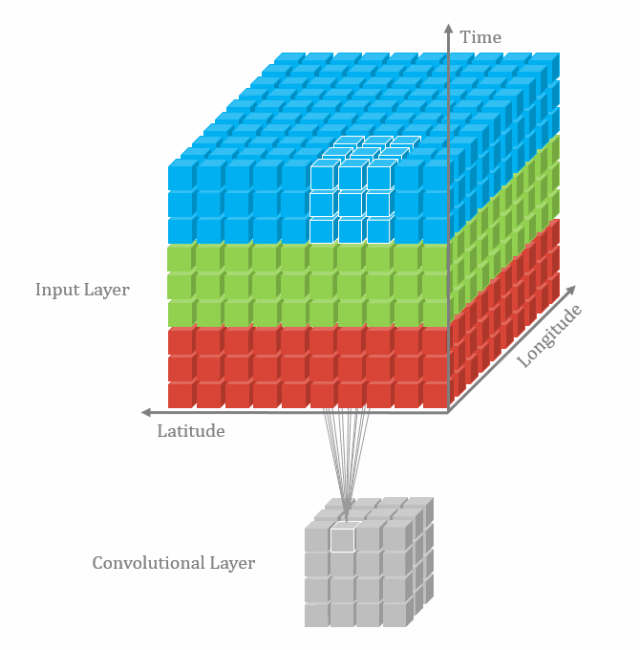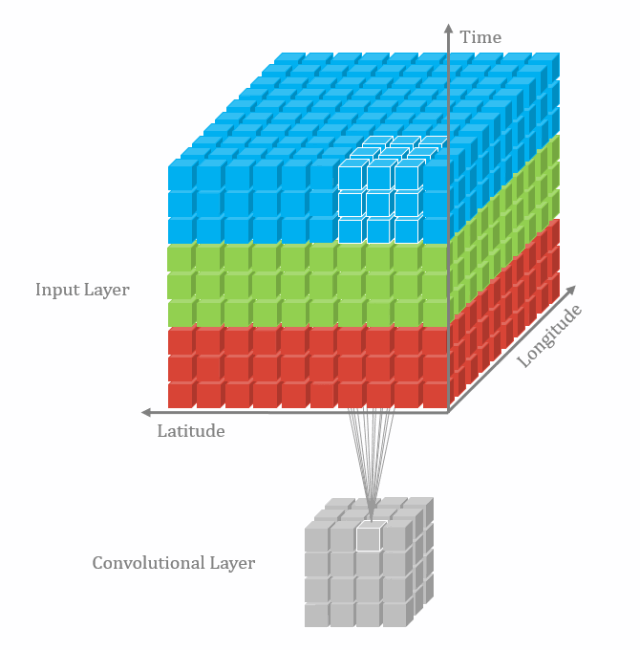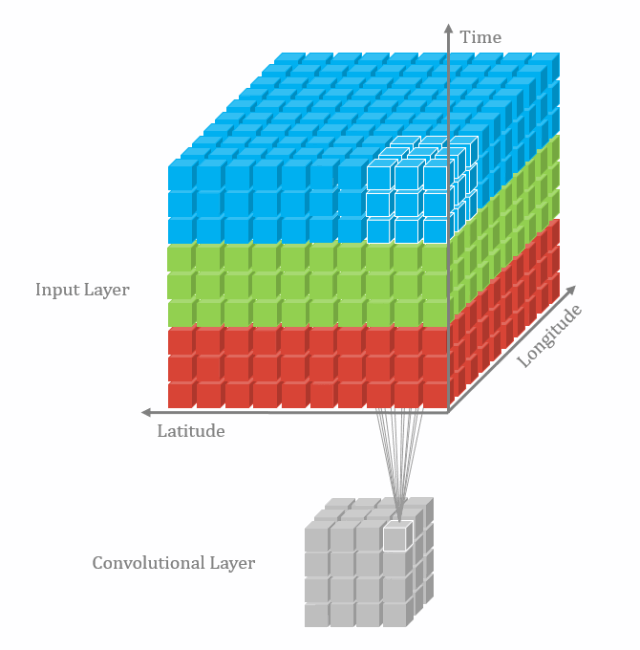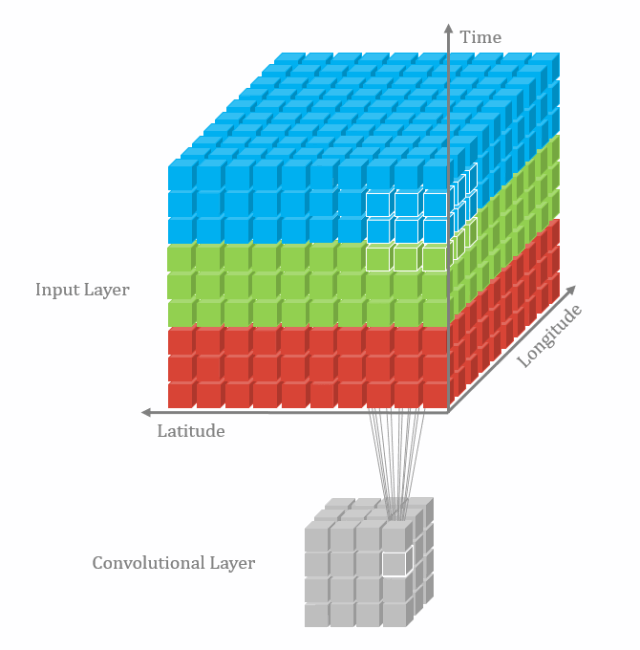
个人理解:
- 三维卷积可以同时提取三个维度的数据的特征,能同时进行空间和空间特征表示,但数据计算量要比二维卷积大不少;
- 由于能处理三维的数据特征,所以三维卷积可以用来处理:
- 视频上的连续帧
- 立体图像中的“图层”(类似于高光谱图像)…
2、每次分类的结果为什么都不一样?
(1)神经网络算法初始化随机权重,因此用同样的数据训练同一个网络会得到不同的结果。
(2)个人感觉,在网络中,还能牵扯到随机性的部分,就是那个Dropout了。在训练模式中,采用了Dropout使得网络在训练的时候,抗噪声能力更强,防止过拟合。但是在测试模型的时候,随机的drop,就会导致最终结果的不一致。为了解决这个问题,在训练模型的时候要加上model.train()开启drop;在测试模型的时候加上model.eval()关掉drop,以此来保持结果一致。
3、能不能使用注意力机制,进一步提升高光谱图像的分类性能?
注意力机制的加入,相当于让网络对某些特征有了更高的权重,使网络更加有侧重的学习,以此提高网络的学习能力。
我在第一个2D卷积之前添加了一层注意力机制来试试效果
##重新定义增加了注意力机制的HybridSN 类
class_num = 16
# 通道注意力机制
class ChannelAttention(nn.Module):
def __init__(self, in_planes, ratio=16):
super(ChannelAttention, self).__init__()
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.max_pool = nn.AdaptiveMaxPool2d(1)
self.fc1 = nn.Conv2d(in_planes, in_planes // 16, 1, bias=False)
self.relu1 = nn.ReLU()
self.fc2 = nn.Conv2d(in_planes // 16, in_planes, 1, bias=False)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
avg_out = self.fc2(self.relu1(self.fc1(self.avg_pool(x))))
max_out = self.fc2(self.relu1(self.fc1(self.max_pool(x))))
out = avg_out + max_out
return self.sigmoid(out)
# 空间注意力机制
class SpatialAttention(nn.Module):
def __init__(self, kernel_size=7):
super(SpatialAttention, self).__init__()
assert kernel_size in (3, 7), 'kernel size must be 3 or 7'
padding = 3 if kernel_size == 7 else 1
self.conv1 = nn.Conv2d(2, 1, kernel_size, padding=padding, bias=False)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
avg_out = torch.mean(x, dim=1, keepdim=True)
max_out, _ = torch.max(x, dim=1, keepdim=True)
x = torch.cat([avg_out, max_out], dim=1)
x = self.conv1(x)
return self.sigmoid(x)
class HybridSN(nn.Module):
def __init__(self, num_classes=16):
super(HybridSN, self).__init__()
self.conv1 = nn.Sequential(nn.Conv3d(1, 8, (7, 3, 3)), nn.BatchNorm3d(8), nn.ReLU())
self.conv2 = nn.Sequential(nn.Conv3d(8, 16, (5, 3, 3)), nn.BatchNorm3d(16), nn.ReLU())
self.conv3 = nn.Sequential(nn.Conv3d(16, 32, (3, 3, 3)), nn.BatchNorm3d(32), nn.ReLU())
self.conv3_2d = nn.Sequential(nn.Conv2d(576, 64, (3,3)), nn.BatchNorm2d(64), nn.ReLU())
self.dense1 = nn.Linear(18496,256)
self.dense2 = nn.Linear(256,128)
self.out = nn.Linear(128, num_classes)
self.drop = nn.Dropout(p=0.4)
self.soft = nn.LogSoftmax(dim=1)
self.relu = nn.ReLU()
self.channel_attention_1 = ChannelAttention(576)
self.spatial_attention_1 = SpatialAttention(kernel_size=7)
self.channel_attention_2 = ChannelAttention(64)
self.spatial_attention_2 = SpatialAttention(kernel_size=7)
def forward(self, x):
out = self.relu(self.conv1(x))
out = self.relu(self.conv2(out))
out = self.relu(self.conv3(out))
# 进行二维卷积,因此把前面的 32*18 reshape 一下,得到 (576, 19, 19)
out = out.view(-1, out.shape[1] * out.shape[2], out.shape[3], out.shape[4])
out = self.channel_attention_1(out) * out
out = self.spatial_attention_1(out) * out
out = self.relu(self.conv3_2d(out))
# flatten 操作,变为 18496 维的向量,
out = out.view(out.size(0), -1)
out = self.dense1(out)
out = self.drop(out)
out = self.dense2(out)
out = self.drop(out)
out = self.out(out)
out = self.soft(out)
return out

个人感觉,:
- 使模型的准确率有了一定的下降,而且也花费了更长的时间…优化效果明显不如之前换softmax函数来的更明显;
- 但是看视觉效果:
 再对比一下之前的:
再对比一下之前的: