参考:
https://blog.csdn.net/zuzhiang/article/details/78134247
https://wenku.baidu.com/view/ec3278ae2f60ddccda38a0f5.html
https://blog.csdn.net/Prasnip_/article/details/83690038
https://blog.csdn.net/ljd201724114126/article/details/80663855
单调栈可以解决:
①可以方便的求出某个数的左边或者右边第一个比它大或者小的元素,总时间复杂度为O(n)。
如何维护:
进栈操作:每次入栈前先检查栈顶元素和进栈元素(x)的大小,如果小于x,就让x直接入栈。如果栈顶元素大于等于x,那么出栈,直到栈空或者栈顶元素小于x。
例题:(POJ 2559)
给出一个柱形统计图,输入宽度为1的矩形的高度,求出这个柱形图中的最大面积的长方形(n<=le5)
例如:2,1,4,5,1,3,3 最打面积为8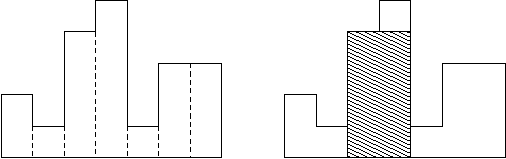
那么如何使用单调栈求解这个呢?
我们可以知道最终的结果是一定是: 在某个区域内,最低矩形的高度x,答案就是x*矩形个数。
那么如何计算x左边的矩形数和x右边的矩形数呢?单调有个left[x]和right[x]数组分别表示x的左边比他大的个数(如果中途出现比x小的就不往左了),和右边比他大的个数(同样如果中途出现比x小的就不往右了),那么就可以解决这个问题了。
具体看代码:
该程序单调栈大致的流程:
每个节点存两个值,一个权值,一个表示第几个数
单调栈中的数都是单调的(这里以单调非递减为例)
当搞完n个数后,还需在最后在压入一个小于题目要求的数,以便将所有数都弹出来。
主要思路:
遍历某个数时,
1.栈空,入队
2.栈不为空,
若大于栈顶元素,直接压入;
否则,将栈顶元素弹掉,直到栈顶元素<=这个数
(在弹的过程中进行操作,依具体题目而定)
// #include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <stack>
#include <cstring>
using namespace std;
#define ll long long
#define p pair<ll , ll>
const int N=1e5+100;;
ll lef[N]; // left[x]以a[x]为矩形的最小的高度的的区域的最左边所在的位置
ll right[N]; // right[x] 表示以a[x]为矩形的最小的高度的的区域的最右边所在的位置
stack<p> sta; // p a的一个数存数据大小,后一个数表示是第几个数
ll a[N];//存放数据
ll solve(int n)
{
ll ans=0;
for(int i=0;i<n+1;i++)//这里为什么要+1呢,是为了栈中元素都弹出来
{
if(sta.empty()) //若为空,压入栈
{
sta.push(make_pair(a[i],i));
lef[i]=i; //最左边就是自己本身
}
else if(a[i]>sta.top().first)
{
sta.push(make_pair(a[i],i));
lef[i]=i;//因此栈中的都是比a[i]小的,故最左边就是自己本身
}
else
{
ll t=i;
while(!sta.empty()&&sta.top().first>a[i])
{
//说明此时sta.top()要弹出,a[i]就是它的最右的边界(不包含a[i]这个数)
// 当然这里可以用right[i]数组先存起来,可能有的题目需要用上
t=min(t,lef[sta.top().second]);// 用来标记以a[i] 为最低高度的局域的 最左边所在的位置
// cout<<"ans,top,lef[i]"<<ans<<" "<<sta.top().first<<" "<<lef[sta.top().second]<<" "<<t<<endl;
ans=max(ans,(sta.top().first)*(i-lef[sta.top().second]));
// left[sta.top().second] 表示sta.top()最左的边界
// (i-left[sta.top().second] 表示的是以sta.top().first为最低高度的局域的 矩形的个数
sta.pop();
}
sta.push(make_pair(a[i],i));
lef[i]=t;
}
}
return ans;
}
int main()
{
int n;
while(~scanf("%d",&n))
{
if(n==0) break;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
a[n]=0;
while(!sta.empty())
sta.pop();
ll ans=solve(n);
printf("%lld\n",ans);
}
return 0;
}
习题:
POJ 2559
题解链接:https://blog.csdn.net/weixin_42373330/article/details/97563113
Gym - 101334F Feel Good
题解链接:https://blog.csdn.net/weixin_42373330/article/details/97609260
单调队列:
队列中元素之间的关系具有单调性,且队首和队尾都可以进行出队操作,只有队尾可以进行入队操作。
用处:
- 对于维护好的单调队列,对内元素是有序的,那么取出最大值(最小值)的复杂度为O(1)
- 可以拿来优化DP(…)
单调队列:通俗的讲就是以一个固定长度的窗口在数列上移动,(这个固定的长度是题目给的,队首元素在队列中的位置与队尾元素在队列的位置之差若大于这个固定长度,就得将队首元素弹出)
具体步骤与单调栈一样,再加个弹队首的操作。
作用:
①获得当前某个范围的最小值或最大值
const int N=3e5+10;
#define ll long long
ll sum[N];
list<int> lis;
int main()
{
int n, m;
while(~scanf("%d%d",&n,&m))
{
lis.clear();
for(int i=1;i<=n;i++)
{
scanf("%lld",&sum[i]);
}
ll mx=sum[1];
lis.push_back(1);
for(int i=2;i<=n;i++)
{
while(!lis.empty()&&i-lis.front()>m) //保证窗口大小
lis.pop_front();
/*mx= max(mx,sum[i]-sum[lis.front()]);依具体而定*/
while(!lis.empty()&&sum[i]<sum[lis.back()])//弹比sum[i]大的
lis.pop_back();
lis.push_back(i);//压入
}
printf("%lld\n",mx);
}
return 0;
}