7.2 枚举排列

直接看问题吧，从问题入手感觉会比较简单。

7.2.1 生成1-n的排列

这个问题就是输出1-n的长度为n的阶乘的一个全排列。那什么叫做全排列呢？我打个比方n=3时，全排列就是(1,2,3)，(1,3,2)，(2,1,3)，(2,3,1)，(3,1,2)，(3,2,1)。你们可以理解为用1-n组成的所有的不同的排列。

我们稍微模拟一下n的情况：先输出以1开头的排列，接下来输出以2开头的排列······输出以n开头的排列。

我们单独拿出一个以i开头的排列的情况：第一数为i，后面的n-1位数实际上就是1-n中除了i的n-1个数的一个全排列。我们用P(n)表示1-n的全排列，p(n)(i)表示1-n的全排列中第一个数字为i的部分。很显然有P(n)=p(n)(1)+p(n)(2)·······+p(n)(n)。我们可以将一个数组长度为n的全排列递归到n个数组长度为n-1的全排列，里面的p(n)(i)可以用同样的方式递归到数组长度为n-2的全排列·······

很显然我们这里就可以用递归的思想去处理这个问题了。代码是比较简单的：

#include<stdio.h>
#include<string.h>
int ans[30],is_exist[30];//0表示可嵌入到数组的数 
void P(int n,int*a,int pos){//pos表示当前递归到第几位 
	if (pos==n) {for (int i=0;i<n;i++) printf("%d ",a[i]); printf("\n");}
	else for (int i=1;i<=n;i++){//将1-n遍历一遍,我们这里用的是桶排序的思想判断有没有取过 
		if (!is_exist[i]) {is_exist[i]=1; a[pos]=i; P(n,a,pos+1);is_exist[i]=0;}
	} 
}
int main(){
	memset(is_exist,0,sizeof(is_exist));
	int n; scanf("%d",&n); P(n,ans,0); return 0; 
} 

需要注意的是，我这里的代码和书上还是有些区别的，书上是向前遍历pos位判断这个数有没有取过，我是通过桶的方法去判断，具体的耗时我没有测过，感觉应该差不多吧(我粗略估算感觉用桶姑且会快一点的样子)。

输出结果姑且没算错：

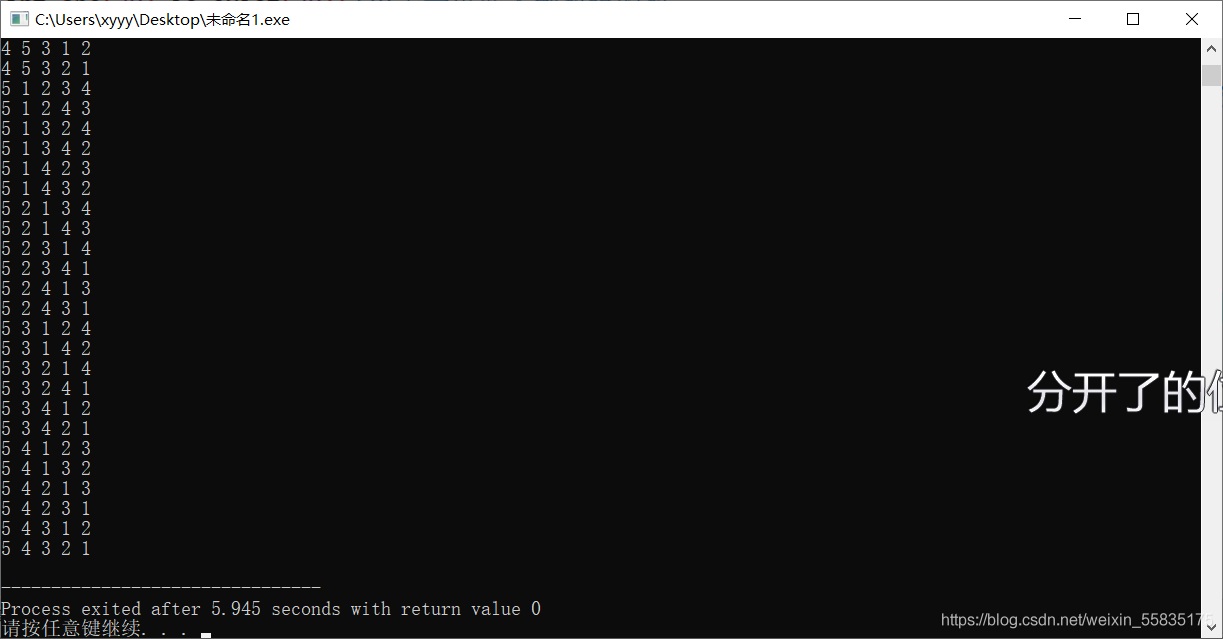
7.2.2 生成可重集的排列

这个问题和上面的1-n的全排列的区别就在于，1-n改为n个数的一个数组，需要对这样n个数的一个数组做全排列。

如果这n个数是n个大小不同的数，我们将这n个数按照从小到大进行排序，桶的i表示这n个数的下标，然后和上面一样进行操作，是没有什么问题的，代码如下：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int ans[30],is_exist[30],a[30];//0表示可嵌入到数组的数 
void P(int n,int*x,int pos){//pos表示当前递归到第几位 
	if (pos==n) {for (int i=0;i<n;i++) printf("%d ",x[i]); printf("\n");}
	else for (int i=0;i<n;i++){//将1-n遍历一遍,我们这里用的是桶排序的思想判断有没有取过 
		if (!is_exist[i]) {is_exist[i]=1; x[pos]=a[i]; P(n,x,pos+1);is_exist[i]=0;}
	} 
}
int main(){
	memset(is_exist,0,sizeof(is_exist));
	int n; scanf("%d",&n); for (int i=0;i<n;i++) scanf("%d",&a[i]); 
	sort(a,a+n); P(n,ans,0); return 0;
} 

但如果这n个数中有若干个数大小相等，就会出现一些问题，比如1,1,1，应该输出的结果是一组3个1，但是按照我们那样做的话，第一个1，第二个1和第三个1被看作了不同的三个数，所以理论上我们会输出6组3个1。

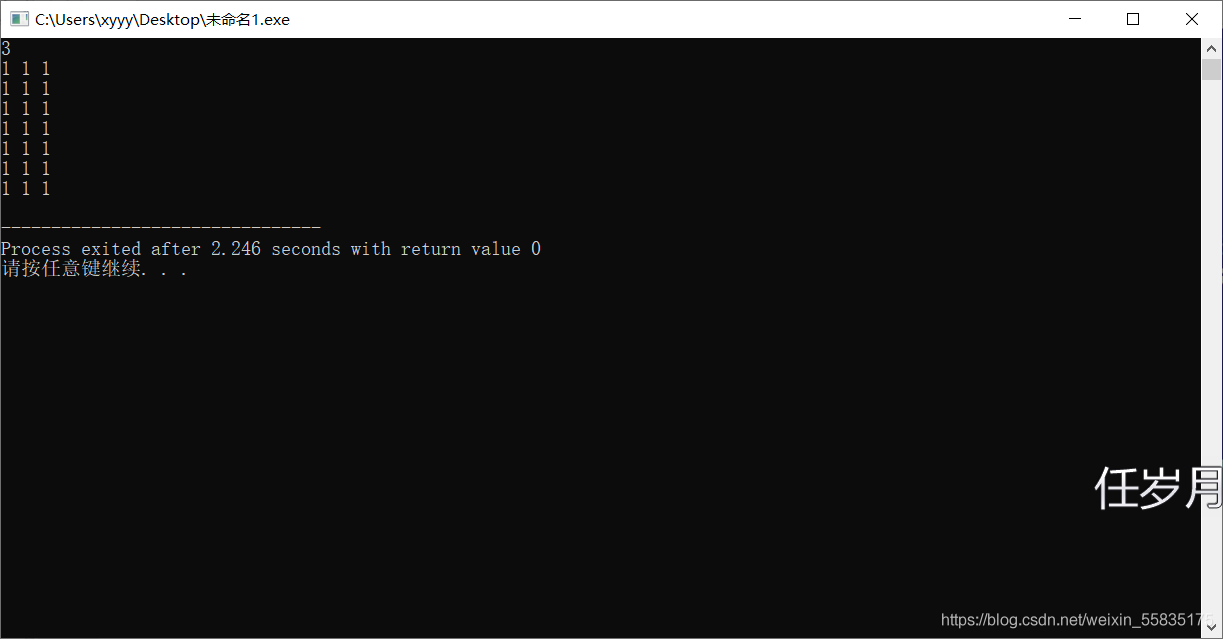
这里书上提供了一种非常美妙的方法，代码如下：

#include<cstdio>
#include<algorithm> 
using namespace std;
int ans[30],a[30]; 
void P(int n,int*x,int pos){//pos依旧表示当前递归到第几位 
	if (pos==n) {for (int i=0;i<n;i++) printf("%d ",x[i]); printf("\n");}
	else for (int i=0;i<n;i++){
		if (!i||(a[i]!=a[i-1])){//这里大家仔细一点的话可以发现,比起桶的思路
		//这里并没有对已经放入答案数组的数据进行标记,而是对准备放入答案数组的数据进行计次 
			int c1=0,c2=0;//c1表示a[i]中目前已经在答案数组中出现的次数,c2表示a[i]在整个数组中出现的次数
			for (int j=0;j<pos;j++) if (x[j]==a[i]) c1++;
			for (int j=0;j<n;j++) if (a[i]==a[j]) c2++;
		//如果c1==c2(大于显然不可能),那么代表这个数已经取完了,那么就不会再放入到答案数组中
		//然而对于a数组中相同的数,例如2,3,3,3,4,实际上并不是将3个不同位置上的3放入答案数组
		//而是将第一次出现的3三次放入答案数组中不同的位置 
			if (c1<c2) {x[pos]=a[i];P(n,x,pos+1);}
		}
	} 
}
int main(){
	int n; scanf("%d",&n); for (int i=0;i<n;i++) scanf("%d",&a[i]); 
	sort(a,a+n); P(n,ans,0); return 0;
} 

结果如下：

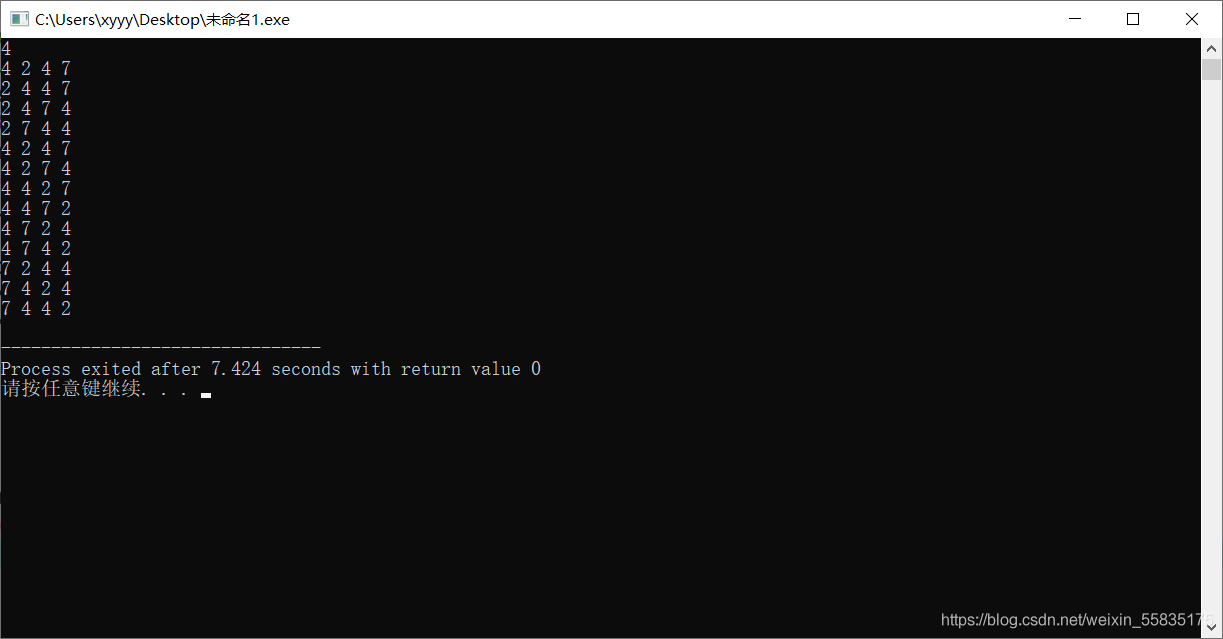
看起来对原本的代码只有微小的改动，但实际上在(判重)思路上已经有了本质上的区别。

7.2.3 解答树

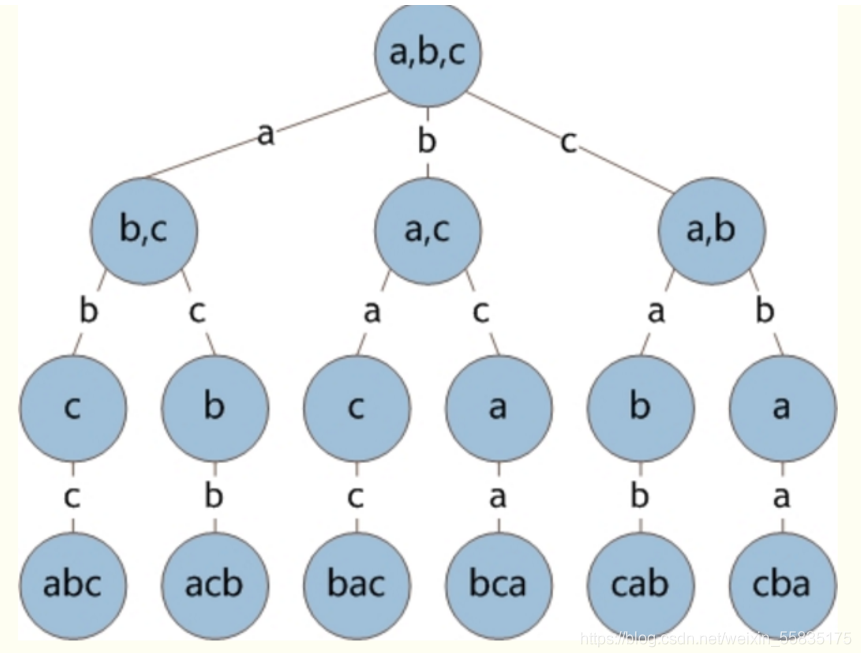
网上随便偷了个图，实际上就是我们分析过程的树状表示，如果熟悉前面dfs的同学(好的，你不熟悉)其实可以发现，我在前面的代码，写的和树的dfs是非常相似的。还有一些性质和我们这里的学习没什么关系，就不做赘述了。

7.2.4 下一个排列

我们之前花了很大的篇章介绍全排列的编写方法，事实上C++的STL中提供了一个库函数next_permutation可以直接得到当前序列在所在全排列的下一个排列，代码如下：

#include<cstdio>
#include<algorithm> 
using namespace std;
int main(){
	int n,a[20]; scanf("%d",&n); for (int i=0;i<n;i++) scanf("%d",&a[i]); 
	next_permutation(a,a+n); 
	for (int i=0;i<n;i++) printf("%d ",a[i]);
	return 0;
} 

这里的next_permuation即表示将a数组的n个数转化为下一个排列，我们可以测试一下看看：

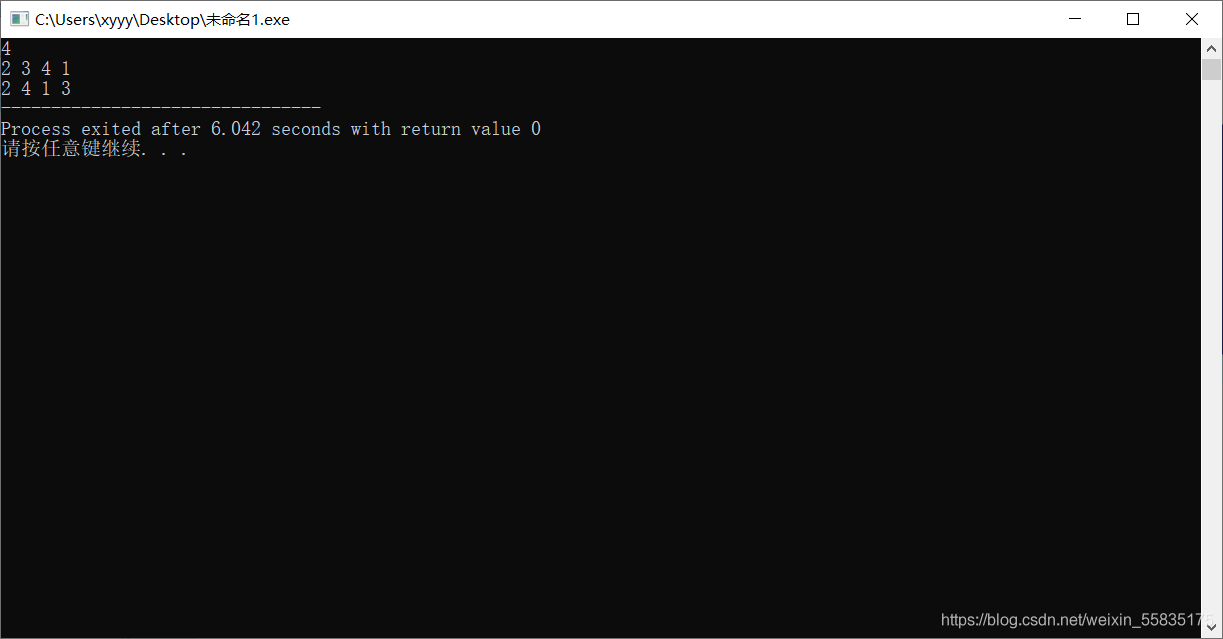
如果前面的代码都是自己写的，我们显然可以知道2 4 1 3是2 3 4 1在全排列中的下一个排列。并且这个函数同样适用于第二个问题，可重集的排列。

那如果a数组当前的排列即是全排列的最后一个呢？

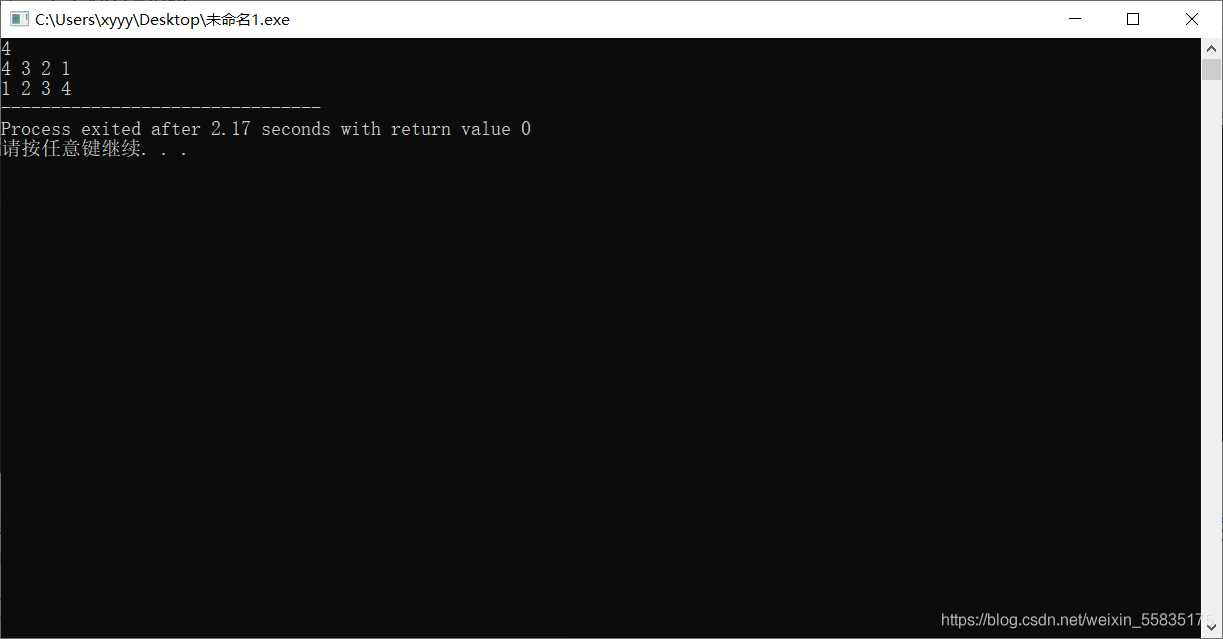
“地球是圆的哦”