强化学习之 PPO 算法
转载文章来源:飞多多
PPO整体思路–PG算法
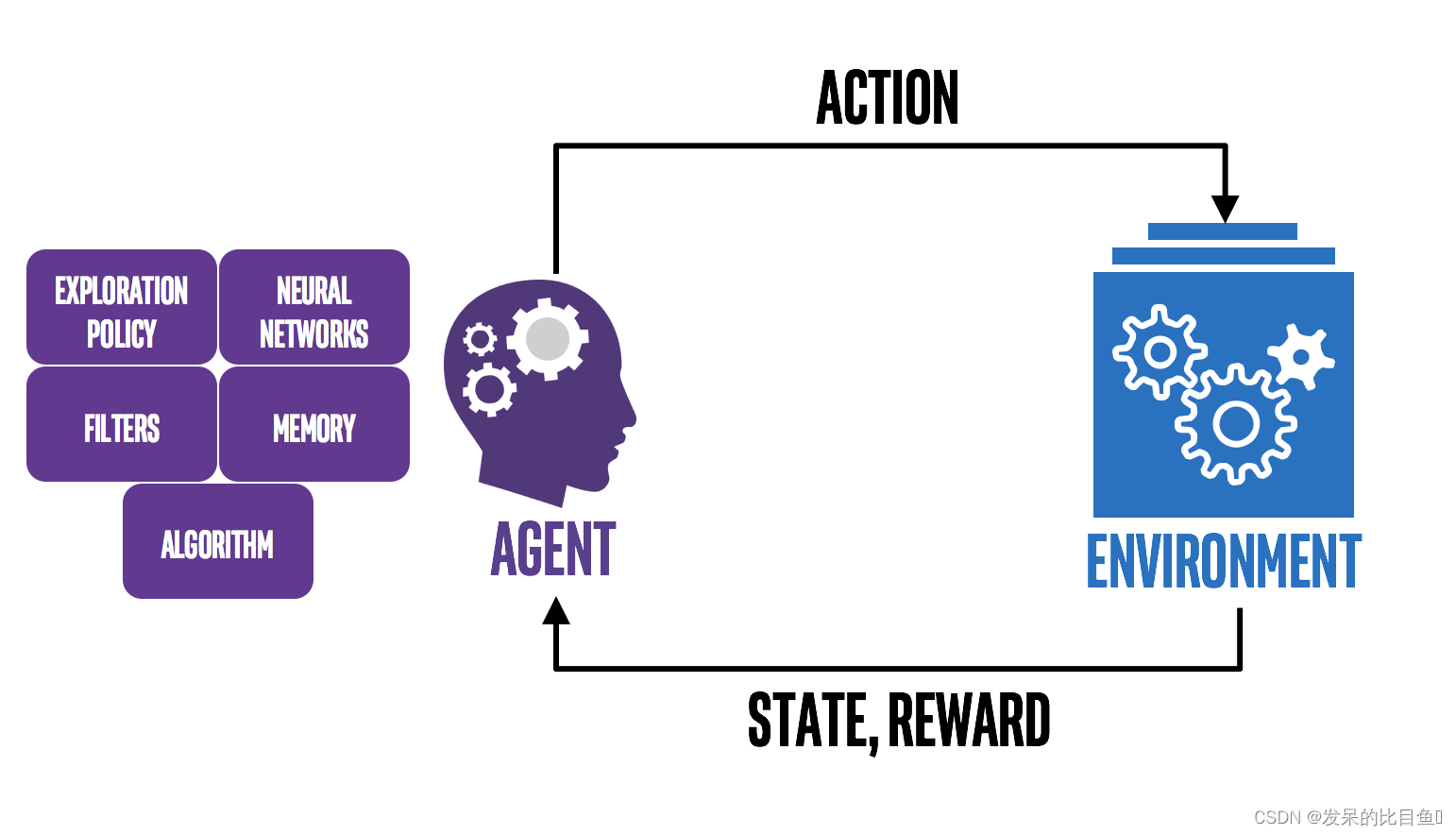
强化学习中,我们有一个Agent作为我们的智能体,它根据策略 π \piπ,在不同的环境状态s ss下选择相应的动作来执行,环境根据Agent的动作,反馈新的状态以及奖励,Agent又根据新的状态选择新的动作,这样不停的循环,知道游戏结束,便完成了eposide。在深度强化学习中,策略π \piπ是由神经网络构成,神经网络的参数为θ \thetaθ,表示成 。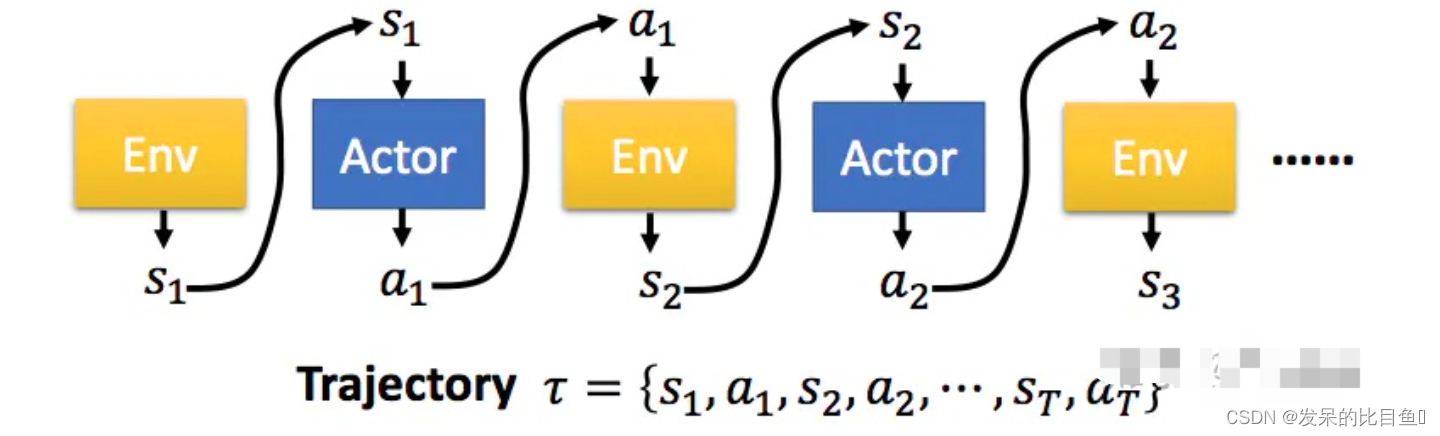
一个完整的eposide序列,用τ \tauτ来表示。而一个特定的τ \tauτ序列发生的概率为: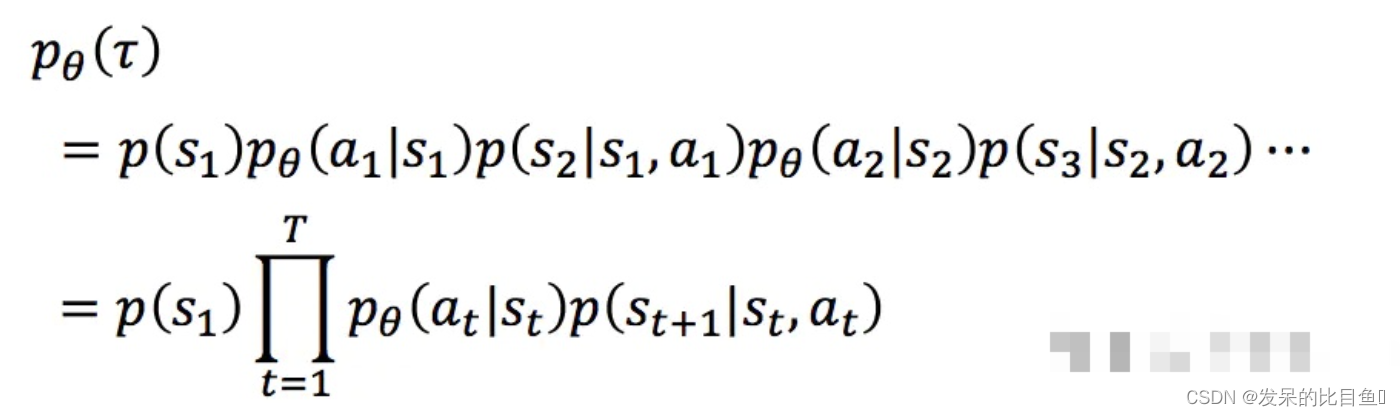
对于一个完整的τ \tauτ序列,他在整个游戏期间获得的总的奖励用R ( τ ) R(\tau)R(τ)来表示。对于给定参数θ \thetaθ的策略,我们评估其应该获得的每局中的总奖励是:对每个采样得到的的 τ \tauτ序列(即每一局)的加权和, 即: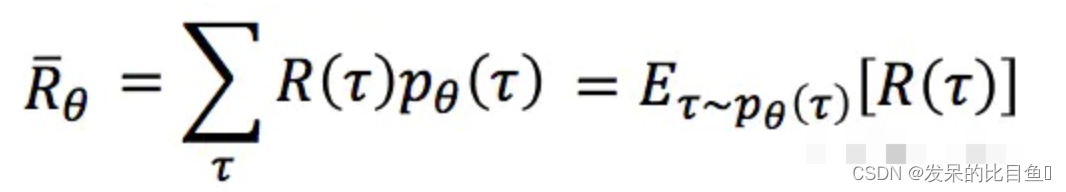
这里的R ˉ θ \bar{R}_{\theta}Rˉθ是在当前策略参数θ \thetaθ下,从一局游戏中得到的奖励的期望的无偏估计。
因此,对于一个游戏,我们自然希望通过调整策略参数θ \thetaθ,得到的R ˉ θ \bar{R}_{\theta}Rˉθ越大越好,因为这意味着,我们选用的策略参数能平均获得更多奖励。这个形式自然就很熟悉了。调整θ \thetaθ, 获取更大的R ˉ θ \bar{R}_{\theta}Rˉθ, 这个很自然的就想到梯度下降的方式来求解。于是用期望的每局奖励对θ \thetaθ求导:
在这个过程中,第一个等号是梯度的变换;第二三个等号是利用了log函数的特性;第四个等号将求和转化成期望的形式;期望又可以由我们采集到的数据序列进行近似;最后一个等号是将每一个数据序列展开成每个数据点上的形式:

之所以把R RR提出来,因为这样理解起来会更直观一点。形象的解释这个式子就是:每一条采样到的数据序列都会希望θ \thetaθ的向着自己的方向进行更新,总体上,我们希望更加靠近奖励比较大的那条序列(效果好的话语权自然要大一点嘛),因此用每条序列的奖励来加权平均他们的更新方向。比如我们假设第三条数据的奖励很大,通过上述公式更新后的策略,使得p ( a t 3 , s t 3 ) p(a_t^3,s_t^3)p(at3,st3)发生的概率更大,以后再遇到s t 3 s^3_tst3这个状态时,我们就更倾向于采取a t 3 a_t^3at3这个动作,或者说以后遇到的状态和第三条序列中的状态相同时,我们更倾向于采取第三条序列曾经所采用过的策略。具体的算法伪代码是: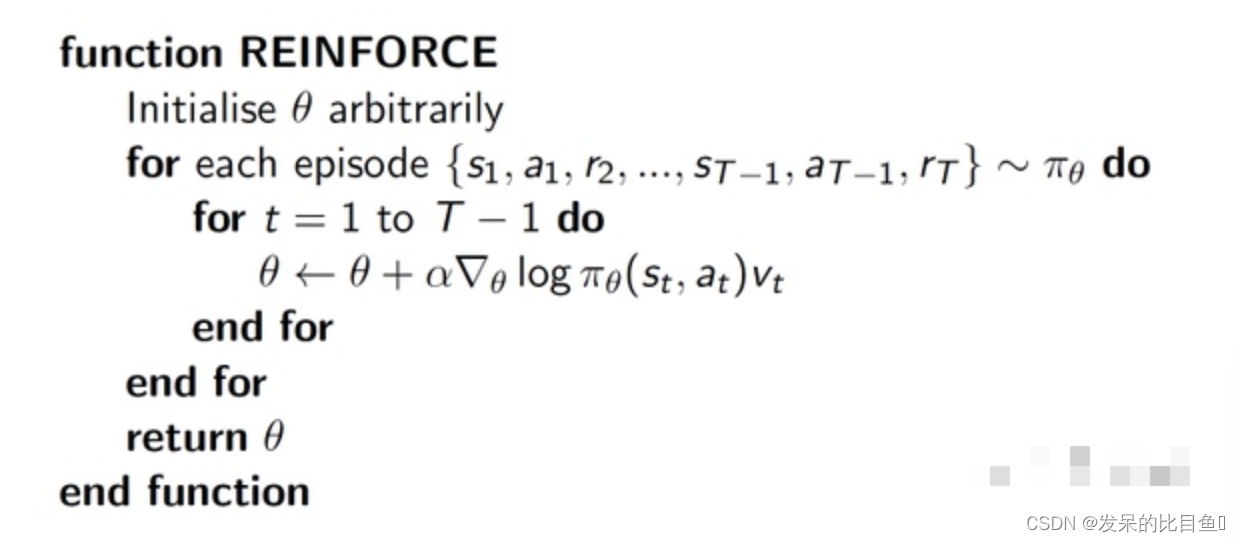
以上,就构成了梯度和采集到的数据序列的近似关系。有了梯度方向和采集的数据序列的关系,一个完整的PG方法就可以表示成: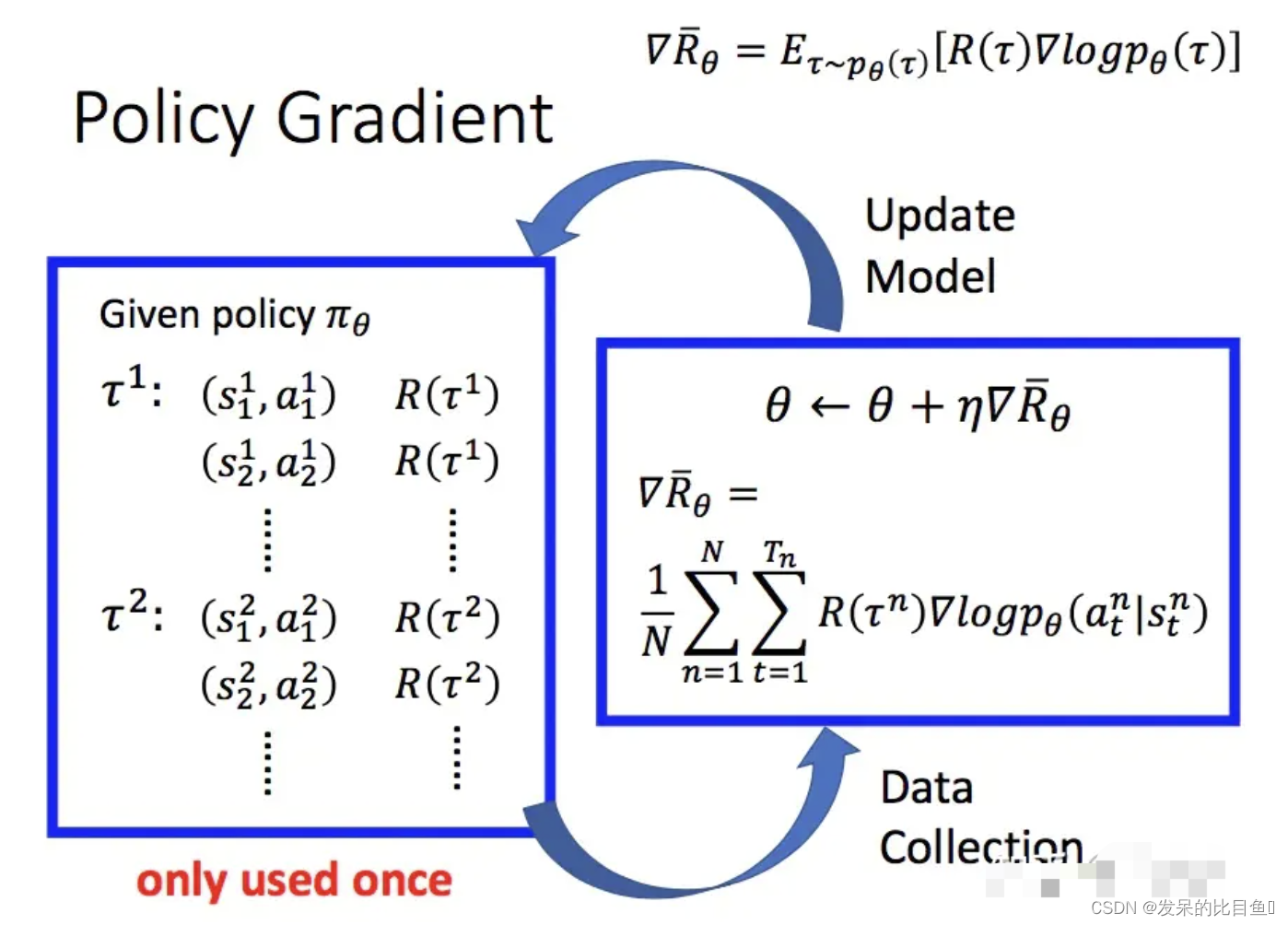
我们首先采集数据,然后基于前面得到的梯度提升的式子更新参数,随后再根据更新后的策略再采集数据,再更新参数,如此循环进行。注意到图中的大红字only used once,因为在更新参数后,我们的策略已经变了,而先前的数据是基于更新参数前的策略得到的
PGTips方法:
增加一个基线
在上面的介绍方法中PG在更新的时候的基本思想就是增大奖励大的策略动作出现的概率,减小奖励小的策略动作出现的概率。但是当奖励的设计不够好的时候,这个思路就会有问题。极端一点的是:无论采取任何动作,都能获得正的奖励。但是这样,对于那些没有采样到的动作,在公式中这些动作策略就体现为0奖励。则可能没被采样到的更好的动作产生的概率就越来越小,使得最后,好的动作反而都被舍弃了。这当然是不对的。于是我们引入一个基线,让奖励有正有负,一般增加基线的方式是所有采样序列的奖励的平均值: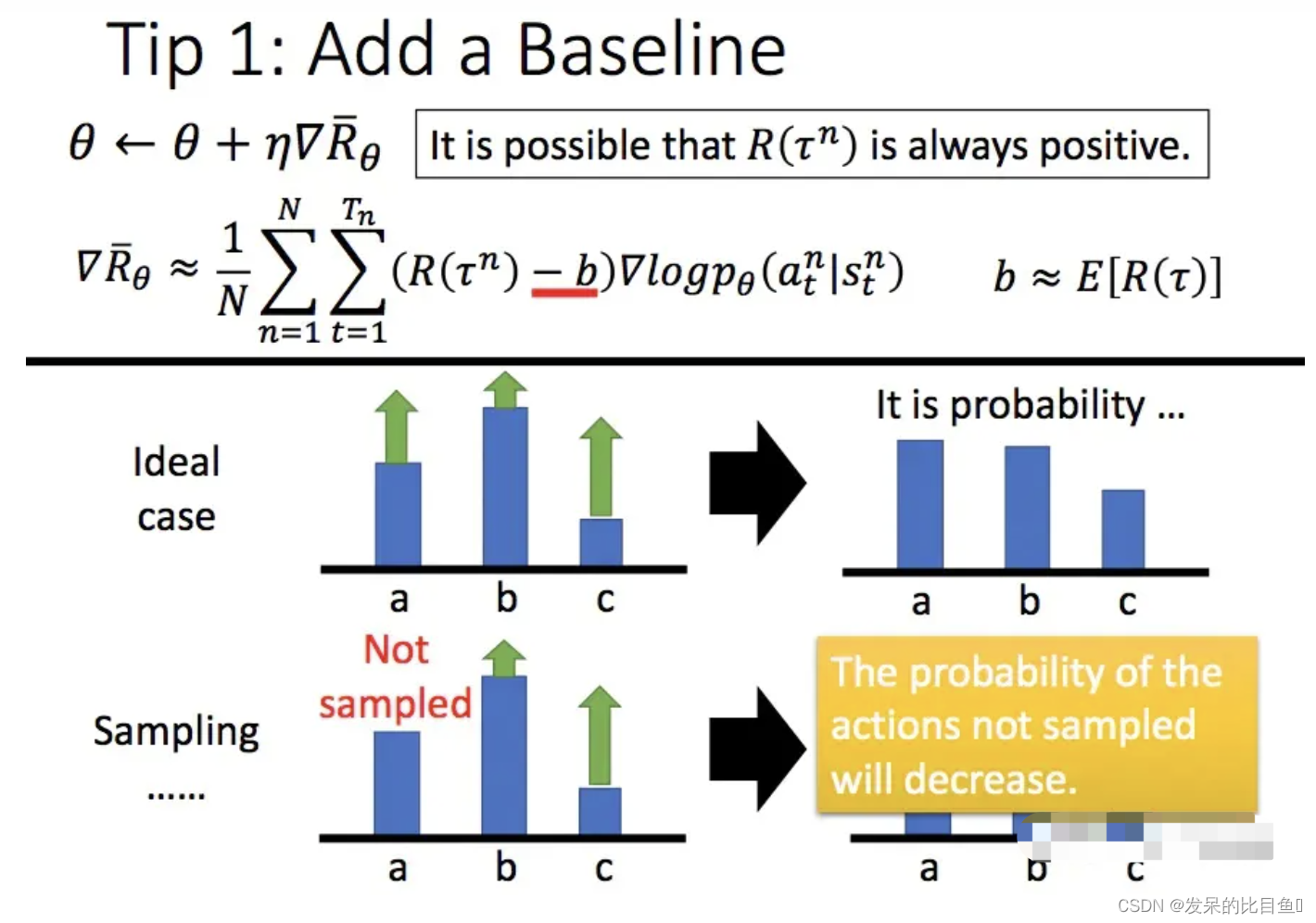
折扣因子
这个很容易理解,就像买股票一样,同样一块钱,当前的一块钱比未来期望的一块钱更具有价值。因此在强化学习中,对未来的奖励需要进行一定的折扣:
使用优势函数
之前用的方法,对于同一个采样序列中的数据点,我们使用相同的奖励R ( τ ) R(\tau)R(τ)(见公式1)。这样的做法实在有点粗糙,更细致的做法是:将这里的奖励替换成关于s t , a t s_t, a_tst,at的函数,我们吧这个函数叫优势函数, 用A θ ( s t , a t ) A^{\theta}(s_t, a_t)Aθ(st,at)来表示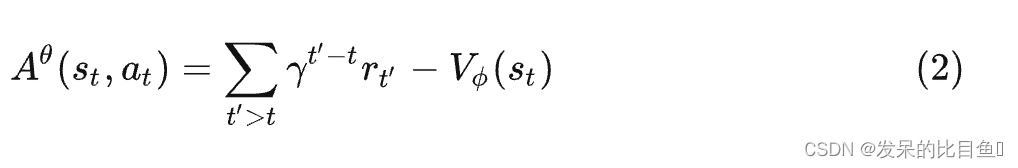
其中V ϕ ( s t ) V_{\phi}(s_t)Vϕ(st)是通过critic来计算得到的,它由一个结构与策略网络相同但参数不同的神经网络构成,主要是来拟合从s t s_tst到终局的折扣奖励。 A θ A^{\theta}Aθ前半部分是实际的采样折扣奖励,后半部分是拟合的折扣奖励。 A θ A^{\theta}Aθ表示了s t s_tst下采取动作a t a_tat ,实际得到的折扣奖励相对于模拟的折扣奖励下的优势,因为模拟的折扣奖励是在 s t s_tst所有采集过的动作的折扣奖励的拟合(平均),因此这个优势函数也就代表了采用动作 a t a_tat相对于这些动作的平均优势。这个优势函数由一个critic(评价者)来给出。
具体来说,譬如在 s t s_tst, n nn个不同采样样本中分别选用了动作α 1 , α 2 , . . . , α n \alpha_1, \alpha_2,...,\alpha_nα1,α2,...,αn,分别得到折扣奖励(从s t s_tst到终局)是 γ 1 , γ 2 , γ 3 , . . . , γ n \gamma_1,\gamma_2,\gamma_3,...,\gamma_nγ1,γ2,γ3,...,γn, 因为是拟合折扣奖励,所以它表示了在 下得到的折扣奖励的期望,我们用γ i \gamma_iγi, i = 1 , 2 , . . . , n i=1,2,...,ni=1,2,...,n , 作为特征去拟合,拟合好后,V ϕ ( s t ) V_{\phi}(s_t)Vϕ(st)就代表了的价值(或者说代表了其获得折扣奖励的期望)。那么(2)式就表示了 a t a_tat相对于α 1 , α 2 , . . . , α n \alpha_1, \alpha_2,...,\alpha_nα1,α2,...,αn这些动作的平均优势。
PPO算法
接着上面的讲,PG方法一个很大的缺点就是参数更新慢,因为我们每更新一次参数都需要进行重新的采样,这其实是中on-policy的策略,即我们想要训练的agent和与环境进行交互的agent是同一个agent;与之对应的就是off-policy的策略,即想要训练的agent和与环境进行交互的agent不是同一个agent,简单来说,就是拿别人的经验来训练自己。举个下棋的例子,如果你是通过自己下棋来不断提升自己的棋艺,那么就是on-policy的,如果是通过看别人下棋来提升自己,那么就是off-policy的:
那么为了提升我们的训练速度,让采样到的数据可以重复使用,我们可以将on-policy的方式转换为off-policy的方式。即我们的训练数据通过另一个相同结构的网络(对应的网络参数为θ’)得到
重要性采样

这里的重要采样其实是一个很常用的思路。在其他很多算法(诸如粒子滤波等)中也经常用到。先引入问题:对于一个服从概率p分布的变量x, 我们要估计f(x) 的期望。直接想到的是,我们采用一个服从p的随机产生器,直接产生若干个变量x的采样,然后计算他们的函数值f(x),最后求均值就得到结果。但这里有一个问题是,对于每一个给定点x,我们知道其发生的概率,但是我们并不知道p的分布,也就无法构建这个随机数发生器。因此需要转换思路:从一个已知的分布q中进行采样。通过对采样点的概率进行比较,确定这个采样点的重要性。也就是上图所描述的方法。
当然通过这种采样方式的分布p和q不能差距过大,否则,会由于采样的偏离带来谬误。即如下图: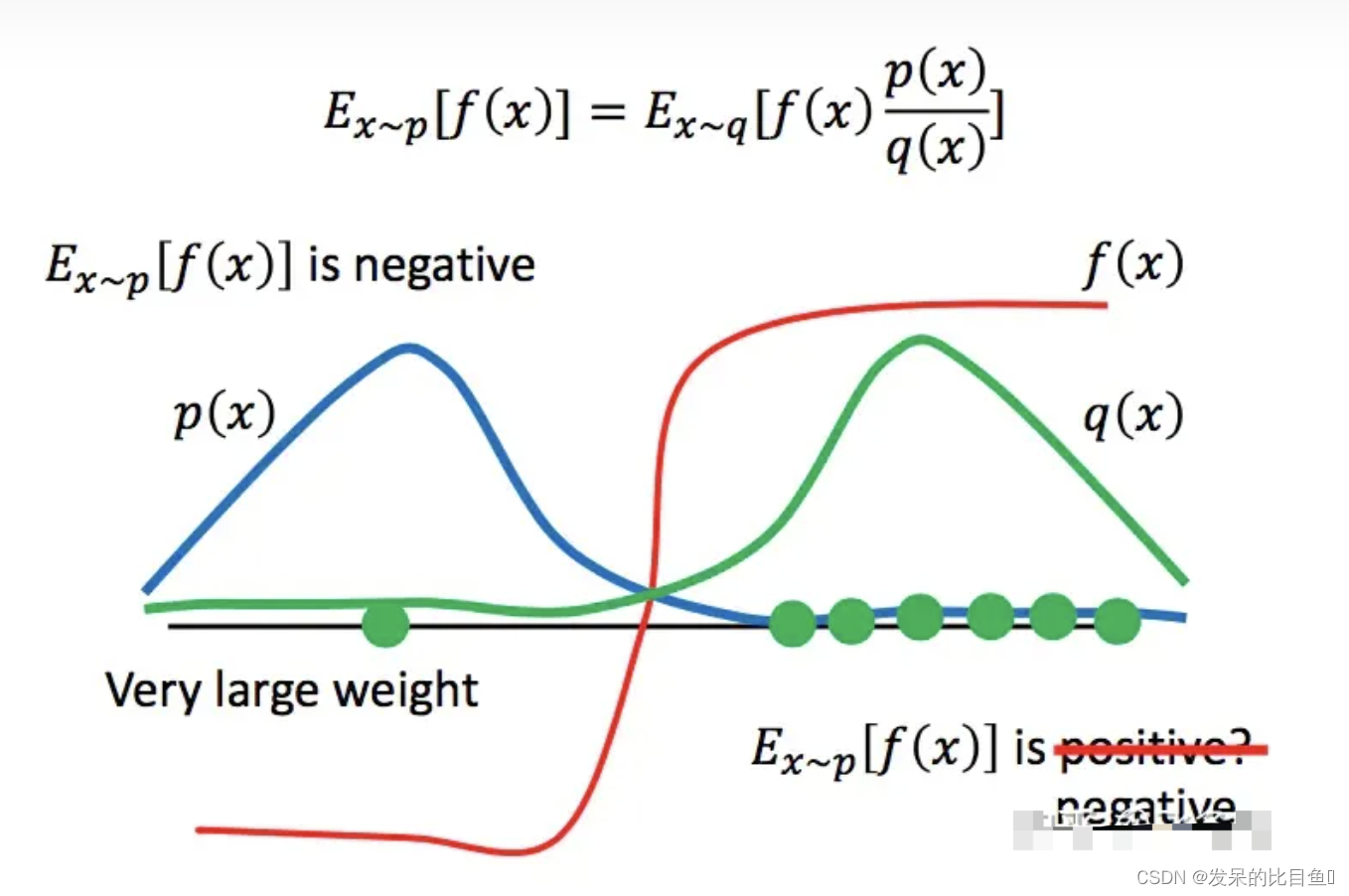
回到PPO中,我们之前的PG方法每次更新参数后,都需要重新和环境进行互动来收集数据,然后用的数据进行更新,这样,每次收集的数据使用一次就丢掉,很浪费,使得网络的更新很慢。于是我们考虑把收集到数据进行重复利用。假设我们收集数据时使用的策略参数是θ ′ \theta'θ′ ,此时收集到的数据τ \tauτ保存到记忆库中,但收集到足够的数据后,我们对参数按照前述的PG方式进行更新,更新后,策略的参数从θ ′ ⟶ θ \theta' \longrightarrow \thetaθ′⟶θ,此时如果采用PG的方式,我们就应该用参数θ \thetaθ的策略重新收集数据,但是我们打算重新利用旧有的数据再更新更新θ \thetaθ 。注意到我我们本来应该是基于θ \thetaθ的策略来收集数据,但实际上我们的数据是由 θ ′ \theta'θ′收集的,所以就需要引入重要性采样来修正这二者之间的偏差,这也就是前面要引入重要性采样的原因。
利用记忆库中的旧数据更新参数的方式变为:
PPO 的前身是 TRPO(Trust Region Policy Optimization),TRPO 与 PPO 之间的区别在于 TRPO 使用了 KL 散度作为约束条件,虽然损失函数是等价的,但是这种表示形式更难计算,所以较少使用。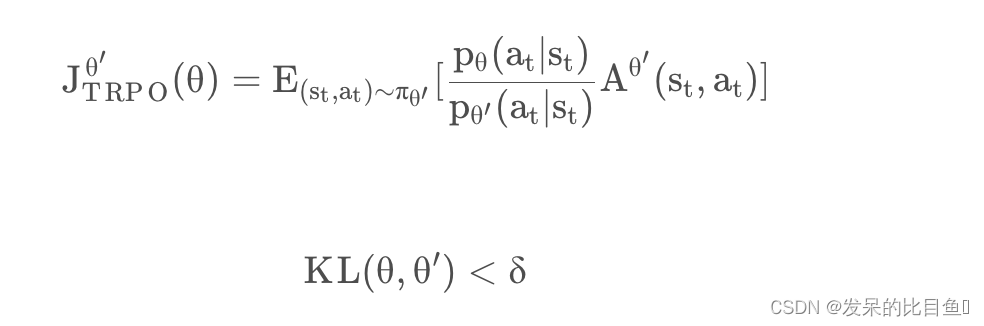
当然,这种方式还是比较原始的,我们通过引入Tips中的优势函数,更精细的控制更细,则更新的梯度变为: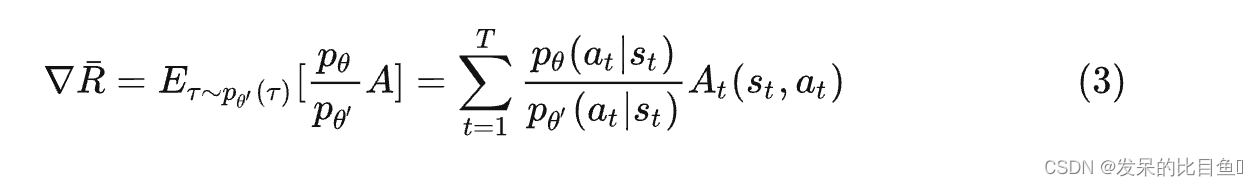
同时,根据重要性采样来说, p θ p_{\theta}pθ和p θ ′ p_{\theta'}pθ′不能差太远了,因为差太远了会引入谬误,所以我们要用KL散度来惩罚二者之间的分布偏差。所以就得到了: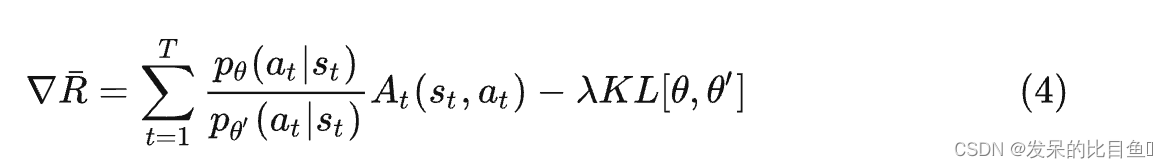
PPO 在训练时可以采用适应性的 KL 惩罚因子:当 KL 过大时,增大 β \betaβ 的值来增加惩罚力度;当 KL 过小时,减小 β \betaβ 值来降低惩罚力度。即:
这里再解释一下优势函数(2)的构成: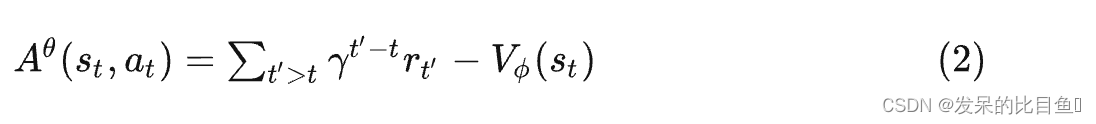
其中前半部分就是我们收集到的数据中的一个序列τ \tauτ中的某一个动作点之后总的折扣奖励。后半部分是critic网络对s t s_tst这个状态的评价。critic网络我们可以看成是一个监督学习网络,他的目的是估计从一个状态s t s_tst到游戏结束能获得的总的折扣奖励,相当于对s t s_tst这个状态的一个评估。从另一个角度看,这里的V ϕ ( s t ) V_{\phi}(s_t)Vϕ(st)也可以看成是对s t s_tst这个状态的后续所以折扣奖励的期望,这就成为了前面Tips中的奖励的基准。
既然是监督学习,我们对V ϕ ( . ) V_{\phi}(.)Vϕ(.)的训练就是对每一个数据序列中的每一个动作点的后续折扣奖励作为待学习的特征,来通过最小化预测和特征之间的误差来更新参数。
通过以上,我们可以看到PPO的更新策略其实有三套网络参数:
一套策略参数θ \thetaθ,他与环境交互收集批量数据,然后批量数据关联到θ \thetaθ的副本中。他每次都会被更新。
一套策略参数的副本θ ′ \theta'θ′,他是策略参数与环境互动后收集的数据的关联参数,相当于重要性采样中的q分布。
一套评价网络的参数ϕ \phiϕ,他是基于收集到的数据,用监督学习的方式来更新对状态的评估。他也是每次都更新。
伪代码

PPO2 算法
PPO2 在 PPO 的基础上去除了 KL 散度损失函数,但是引入了 Clip 损失函数,当目标函数值低于 1 − ϵ 1 − ϵ1−ϵ 或大于 1 + ϵ 1 + ϵ1+ϵ时进行截断。其损失函数为: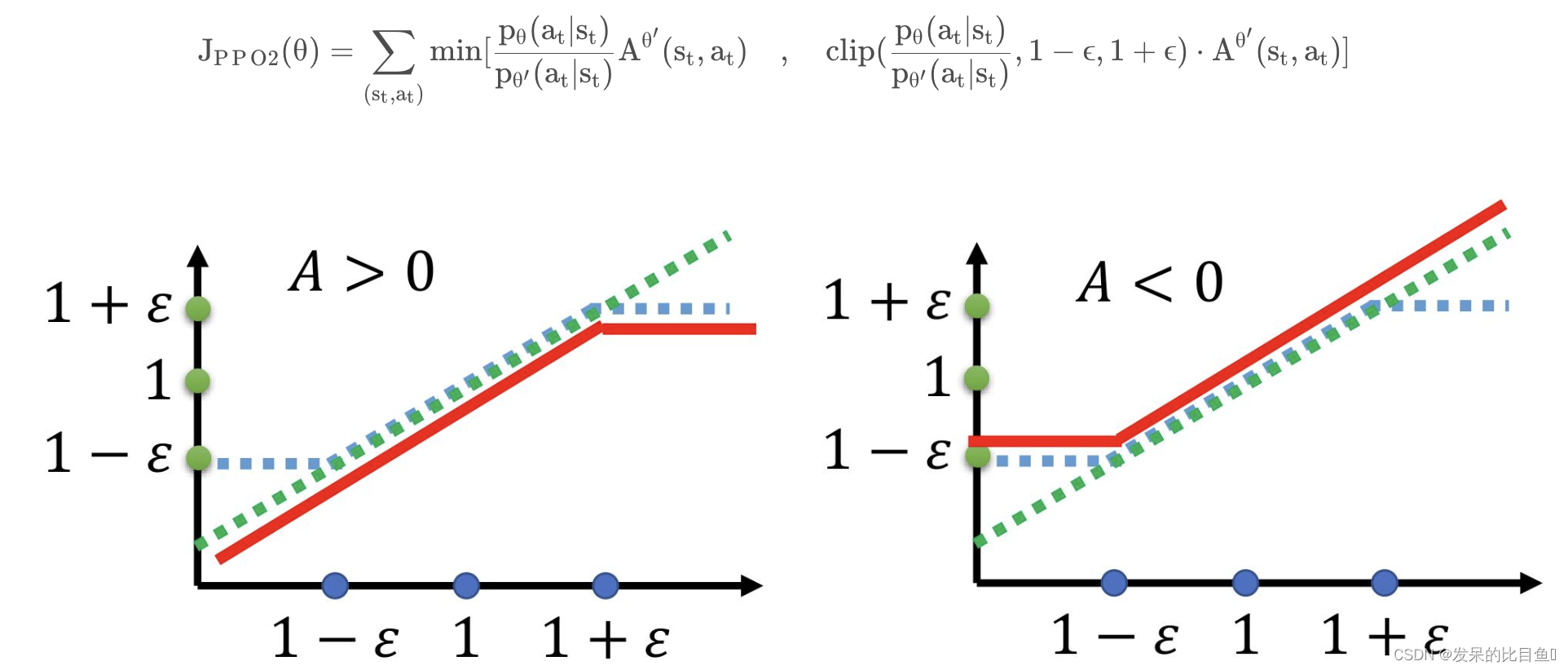
上图中绿色虚线是原始的损失函数,蓝色虚线是 clip 函数,红色实线是实际上的损失函数,当优势函数 A 的值为正数或负数时,实际的损失函数有不同的情况。
代码
# -*- encoding: utf-8 -*-
'''
Filename :ppo.py
Description :
Time :2022/11/07 09:18:07
Author :daiyizheng
Email :387942239@qq.com
Version :1.0
'''
import torch
import torch.nn as nn
from torch.distributions import MultivariateNormal
import gym
import numpy as np
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
class Memory:
def __init__(self):
self.actions = [] # 动作a
self.states = [] # 状态s
self.logprobs = [] # logp_{\theta}(a/s)
self.rewards = [] # 奖励
self.is_terminals = []
def clear_memory(self):
# del语句作用在变量上,而不是数据对象上。删除的是变量,而不是数据。
del self.actions[:]
del self.states[:]
del self.logprobs[:]
del self.rewards[:]
del self.is_terminals[:]
class ActorCritic(nn.Module):
def __init__(self, state_dim, action_dim, action_std):
super(ActorCritic, self).__init__()
# action mean range -1 to 1
self.actor = nn.Sequential( # 演员
nn.Linear(state_dim, 64),
nn.Tanh(),
nn.Linear(64, 32),
nn.Tanh(),
nn.Linear(32, action_dim),
nn.Tanh()
)
# critic 评价者
self.critic = nn.Sequential(
nn.Linear(state_dim, 64),
nn.Tanh(),
nn.Linear(64, 32),
nn.Tanh(),
nn.Linear(32, 1)
)
# 方差
self.action_var = torch.full((action_dim,), action_std * action_std).to(device)
def forward(self):
# 手动设置异常
raise NotImplementedError
def act(self, state, memory):
action_mean = self.actor(state) # old演员拿到ation_mean值,目的是要用这个随机的去逼近真正的选择动作action的高斯分布
cov_mat = torch.diag(self.action_var).to(device) # 取矩阵对角线元素
dist = MultivariateNormal(action_mean, cov_mat) # 生成多元正态分布
action = dist.sample() # 采样点
action_logprob = dist.log_prob(action) # 采样概率分布
memory.states.append(state) #
memory.actions.append(action)
memory.logprobs.append(action_logprob)
return action.detach()
def evaluate(self, state, action):
action_mean = self.actor(state) # 新演员拿到
action_var = self.action_var.expand_as(action_mean)
# torch.diag_embed(input, offset=0, dim1=-2, dim2=-1) → Tensor
# Creates a tensor whose diagonals of certain 2D planes (specified by dim1 and dim2) are filled by input
cov_mat = torch.diag_embed(action_var).to(device)
# 生成一个多元高斯分布矩阵
dist = MultivariateNormal(action_mean, cov_mat)
# 我们的目的是要用这个随机的去逼近真正的选择动作action的高斯分布
action_logprobs = dist.log_prob(action)
# log_prob 是action在前面那个正太分布的概率的log ,我们相信action是对的 ,
# 那么我们要求的正态分布曲线中点应该在action这里,所以最大化正太分布的概率的log, 改变mu,sigma得出一条中心点更加在a的正太分布。
dist_entropy = dist.entropy()
state_value = self.critic(state) # 评价者 V_\phi(s)
return action_logprobs, torch.squeeze(state_value), dist_entropy
class PPO:
def __init__(self, state_dim, action_dim, action_std, lr, betas, gamma, K_epochs, eps_clip):
self.lr = lr
self.betas = betas
self.gamma = gamma
self.eps_clip = eps_clip
self.K_epochs = K_epochs
self.policy = ActorCritic(state_dim, action_dim, action_std).to(device) # V_{\phi}
self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr, betas=betas)
self.policy_old = ActorCritic(state_dim, action_dim, action_std).to(device)
self.policy_old.load_state_dict(self.policy.state_dict()) #V_{\phi'}
self.MseLoss = nn.MSELoss()
def select_action(self, state, memory):
state = torch.FloatTensor(state.reshape(1, -1)).to(device) # s = (1, 24)
return self.policy_old.act(state, memory).cpu().data.numpy().flatten() # 重要性采样, 根据s,在之前的模型中采样
def update(self, memory):
# Monte Carlo estimate of rewards: 奖励的蒙特卡罗估计
rewards = [] #
discounted_reward = 0 # 实际的采样折扣奖励
for reward, is_terminal in zip(reversed(memory.rewards), reversed(memory.is_terminals)): # 从后往前计算
if is_terminal:
discounted_reward = 0
discounted_reward = reward + (self.gamma * discounted_reward) # \sum_{t'>t}\gamma^{t'-t}
rewards.insert(0, discounted_reward)
# Normalizing the rewards: 正则化奖励
rewards = torch.tensor(rewards, dtype=torch.float32).to(device) #
rewards = (rewards - rewards.mean()) / (rewards.std() + 1e-5) # 优势函数 A^{\theta}(s_t, a_t)
# convert list to tensor
# 使用stack可以保留两个信息:[1. 序列] 和 [2. 张量矩阵] 信息,属于【扩张再拼接】的函数;
old_states = torch.squeeze(torch.stack(memory.states).to(device), 1).detach()
old_actions = torch.squeeze(torch.stack(memory.actions).to(device), 1).detach()
old_logprobs = torch.squeeze(torch.stack(memory.logprobs), 1).to(device).detach()
# Optimize policy for K epochs: 优化K个epochs的策略:
for _ in range(self.K_epochs):
# Evaluating old actions and values :
logprobs, state_values, dist_entropy = self.policy.evaluate(old_states, old_actions) # 新演员
# 新演员action的概率 state_values 拟合的折扣奖励 dist_entropy 分布熵
# Finding the ratio (pi_theta / pi_theta__old):
ratios = torch.exp(logprobs - old_logprobs.detach()) # \pi_{\theta}(a_t|s_t) / \pi_{old \theta}(a_t|s_t)
# Finding Surrogate Loss:
advantages = rewards - state_values.detach()
surr1 = ratios * advantages
surr2 = torch.clamp(ratios, 1 - self.eps_clip, 1 + self.eps_clip) * advantages
loss = -torch.min(surr1, surr2) + 0.5 * self.MseLoss(state_values, rewards) - 0.01 * dist_entropy
## 熵 交叉熵 kl散度的关系 D(p||q) = H(p,q) - H(p)
# take gradient step
self.optimizer.zero_grad()
loss.mean().backward()
self.optimizer.step()
# Copy new weights into old policy:
self.policy_old.load_state_dict(self.policy.state_dict())
def main():
############## Hyperparameters ##############
env_name = "BipedalWalker-v3"
render = False
solved_reward = 300 # stop training if avg_reward > solved_reward 贡献值大于xx停止训练
log_interval = 20 # print avg reward in the interval 每20步打印日志
max_episodes = 10000 # max training episodes 最大训练次数
max_timesteps = 1500 # max timesteps in one episode # 一一次的最大时间步长
update_timestep = 4000 # update policy every n timesteps 每n个时间步更新策略
action_std = 0.5 # constant std for action distribution (Multivariate Normal) 作用分布的常数标准差(多元正态)
K_epochs = 80 # update policy for K epochs update policy for K epochs K个epochs的更新策略
eps_clip = 0.2 # clip parameter for PPO PPO的剪辑参数
gamma = 0.99 # discount factor 折扣系数
lr = 0.0003 # parameters for Adam optimizer
betas = (0.9, 0.999)
random_seed = None
#############################################
# creating environment
env = gym.make(env_name)
state_dim = env.observation_space.shape[0] # 环境状态个数
action_dim = env.action_space.shape[0] # 动作个数
if random_seed:
print("Random Seed: {}".format(random_seed))
torch.manual_seed(random_seed)
env.seed(random_seed)
np.random.seed(random_seed)
memory = Memory()
ppo = PPO(state_dim, action_dim, action_std, lr, betas, gamma, K_epochs, eps_clip)
print(lr, betas)
# logging variables
running_reward = 0
avg_length = 0
time_step = 0
# training loop
for i_episode in range(1, max_episodes + 1):
state = env.reset()# 环境状态 (24,)
for t in range(max_timesteps): # 最大深度 \tau
time_step += 1
# Running policy_old:
action = ppo.select_action(state, memory) # p(a/s)
state, reward, done, _ = env.step(action)
# Saving reward and is_terminals:
memory.rewards.append(reward)
memory.is_terminals.append(done) # 是否已经完成
# update if its time 更新
if time_step % update_timestep == 0:
ppo.update(memory)
memory.clear_memory()
time_step = 0
running_reward += reward
if render:
env.render()
if done:
break
avg_length += t
# stop training if avg_reward > solved_reward
if running_reward > (log_interval * solved_reward):
print("########## Solved! ##########")
torch.save(ppo.policy.state_dict(), './PPO_continuous_solved_{}.pth'.format(env_name))
break
# save every 500 episodes
if i_episode % 500 == 0:
torch.save(ppo.policy.state_dict(), './PPO_continuous_{}.pth'.format(env_name))
# logging
if i_episode % log_interval == 0:
avg_length = int(avg_length / log_interval)
running_reward = int((running_reward / log_interval))
print('Episode {} \t Avg length: {} \t Avg reward: {}'.format(i_episode, avg_length, running_reward))
running_reward = 0
avg_length = 0
if __name__ == '__main__':
main()