创建双精度数据
首先创建一些数据,默认情况下为双精度。
Ad = [1 2 0; 2 5 -1; 4 10 -1]
Ad = 3×3
1 2 0
2 5 -1
4 10 -1
转换为单精度
可以使用 single 函数将数据转换为单精度。
A = single(Ad); % or A = cast(Ad,'single');
创建单精度零和一
此外,也可以分别使用函数创建单精度零和一。
n = 1000;
Z = zeros(n,1,'single');
O = ones(n,1,'single');
看一下工作区中的变量。
whos A Ad O Z n
Name Size Bytes Class Attributes
A 3x3 36 single
Ad 3x3 72 double
O 1000x1 4000 single
Z 1000x1 4000 single
n 1x1 8 double
可以看到,部分变量的类型为 single,变量 A(Ad 的单精度版本)需要一半的内存字节数用于存储,因为单精度仅需要四字节(32 位),而双精度需要 8 字节(64 位)。
算术运算和线性代数运算
可以对单精度数据执行标准算术运算和线性代数运算。
B = A' % Matrix Transpose
B = 3x3 single matrix
1 2 4
2 5 10
0 -1 -1
whos B
Name Size Bytes Class Attributes
B 3x3 36 single
可以看出,此操作的结果 B 为单精度。
C = A * B % Matrix multiplication
C = 3x3 single matrix
5 12 24
12 30 59
24 59 117
C = A .* B % Elementwise arithmetic
C = 3x3 single matrix
1 4 0
4 25 -10
0 -10 1
X = inv(A) % Matrix inverse
X = 3x3 single matrix
5 2 -2
-2 -1 1
0 -2 1
I = inv(A) * A % Confirm result is identity matrix
I = 3x3 single matrix
1 0 0
0 1 0
0 0 1
I = A \ A % Better way to do matrix division than inv
I = 3x3 single matrix
1 0 0
0 1 0
0 0 1
E = eig(A) % Eigenvalues
E = 3x1 single column vector
3.7321
0.2679
1.0000
F = fft(A(:,1)) % FFT
F = 3x1 single column vector
7.0000 + 0.0000i
-2.0000 + 1.7321i
-2.0000 - 1.7321i
S = svd(A) % Singular value decomposition
S = 3x1 single column vector
12.3171
0.5149
0.1577
P = round(poly(A)) % The characteristic polynomial of a matrix
P = 1x4 single row vector
1 -5 5 -1
R = roots(P) % Roots of a polynomial
R = 3x1 single column vector
3.7321
1.0000
0.2679
Q = conv(P,P) % Convolve two vectors
Q = 1x7 single row vector
1 -10 35 -52 35 -10 1
R = conv(P,Q)
R = 1x10 single row vector
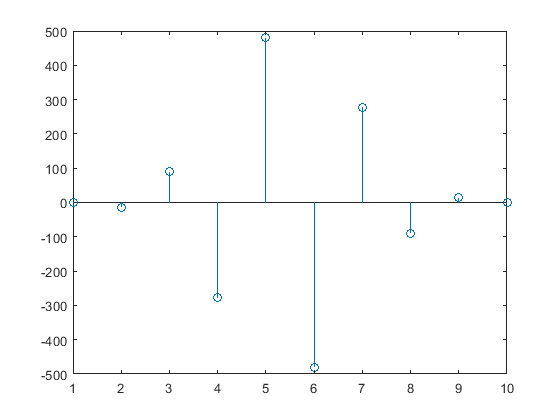
1 -15 90 -278 480 -480 278 -90 15 -1
stem(R); % Plot the result
用于处理单精度或双精度的一个程序
现在来看一个函数,该函数用于计算为使比率小于 single 或 double 数据类型的正确机器精度 (eps),斐波那契数列需要的足够项数。
% How many terms needed to get single precision results?
fibodemo('single')
ans = 19
% How many terms needed to get double precision results?
fibodemo('double')
ans = 41
% Now let's look at the working code.
type fibodemo
function nterms = fibodemo(dtype)
%FIBODEMO Used by SINGLEMATH demo.
% Calculate number of terms in Fibonacci sequence.
% Copyright 1984-2014 The MathWorks, Inc.
fcurrent = ones(dtype);
fnext = fcurrent;
goldenMean = (ones(dtype)+sqrt(5))/2;
tol = eps(goldenMean);
nterms = 2;
while abs(fnext/fcurrent - goldenMean) >= tol
nterms = nterms + 1;
temp = fnext;
fnext = fnext + fcurrent;
fcurrent = temp;
end
请注意,我们初始化了几个变量,即 fcurrent、fnext 和 goldenMean,初始化所用的值取决于输入数据类型,容差 tol 也取决于该类型。与等效的双精度计算相比,单精度要求计算的项较少。