前言
学习一下基础
基本思想
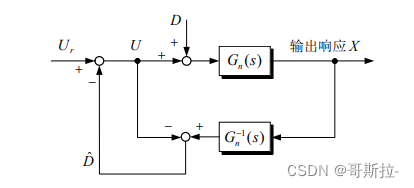
原理框图
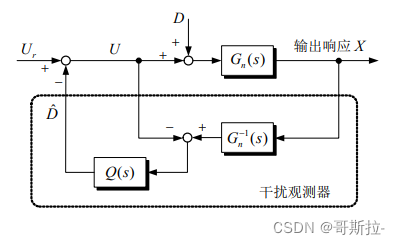
则系统输出X为
X = G n ( s ) U r + G n ( s ) [ 1 − Q ( s ) ] D X=G_n(s)U_r+G_n(s)[1-Q(s)]DX=Gn(s)Ur+Gn(s)[1−Q(s)]D
Q ( s ) Q(s)Q(s) 具有低通滤波特性,其作用在于:
(1)G n G_nGn的相对阶不为0,其逆在物理上不可实现
(2)系统存在不确定性,无法获取被控对象精确地数学模型
(3)系统传感器的测量噪声会影响系统的控制性能
我的问题
1.什么物理上不可实现
我们在设计控制器时,积分在物理上是可实现的,但是微分是不可实现的微分需要用到未来信息,往往用差分代替。对于我们不可实现的名义逆模型 G n − 1 G^{-1}_nGn−1 ,Q ( s ) G n − 1 Q(s)G^{-1}_nQ(s)Gn−1是可以实现的
2.什么是低通滤波
例如:Q ( s ) = a s + a Q(s)=\frac{a}{s+a}Q(s)=s+aa
s = j w → G ( j w ) = a a + j w = a ( a − j w ) ( a + j w ) ( a − j w ) = a 2 a 2 + w 2 + − a w a 2 + w 2 j s=jw\rightarrow G(jw)=\frac{a}{a+jw}=\frac{a(a-jw)}{(a+jw)(a-jw)}=\frac{a^2}{a^2+w^2}+-\frac{aw}{a^2+w^2}js=jw→G(jw)=a+jwa=(a+jw)(a−jw)a(a−jw)=a2+w2a2+−a2+w2awj
∣ G ( j w ) ∣ = 1 1 + w a 2 |G(jw)|=\sqrt{\frac{1}{1+{\frac{w}{a}}^2}}∣G(jw)∣=1+aw21
当w < < a ⟹ ∣ G ( j w ) ∣ → 1 w<<a\implies |G(jw)|\rightarrow 1w<<a⟹∣G(jw)∣→1
当w > > a ⟹ ∣ G ( j w ) ∣ → 0 w>>a\implies |G(jw)|\rightarrow 0w>>a⟹∣G(jw)∣→0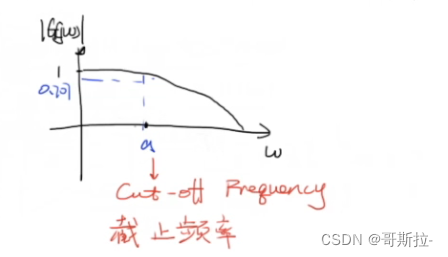
这说明频率越大,振幅响应越小,所以就是典型的低通滤波器
3.在干扰观测器中,截止频率设置得过高会怎么样
上图中D包含了外部干扰和模型不确定性: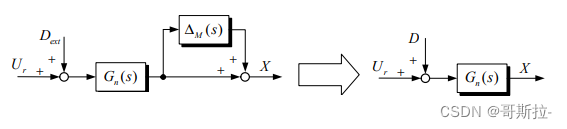
当G p ( s ) = G n ( s ) ( 1 + Δ M ( s ) ) G_p(s)=G_n(s)(1+\Delta M(s))Gp(s)=Gn(s)(1+ΔM(s))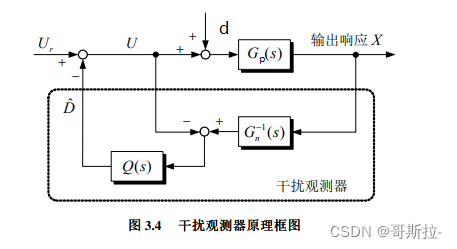
传递函数
S ( s ) = G p G n G n + ( G p − G n ) Q S(s)=\frac{G_pG_n}{G_n+(G_p-G_n)Q}S(s)=Gn+(Gp−Gn)QGpGn
取带有干扰观测器的被控对象的灵敏度函数S ( s ) S(s)S(s)和补灵敏度函数T ( s ) T(s)T(s)
S ( s ) = G n [ 1 − Q ( s ) ] G n ( s ) + [ G p ( s ) − G n ( s ) ] Q ( s ) S(s)=\frac{G_n[1-Q(s)]}{G_n(s)+[G_p(s)-G_n(s)]Q(s)}S(s)=Gn(s)+[Gp(s)−Gn(s)]Q(s)Gn[1−Q(s)]
T ( s ) = 1 − S ( s ) = G n ( s ) Q ( s ) G n ( s ) + [ G p ( s ) − G n ( s ) ] Q ( s ) = G n ( s ) Q ( s ) G n ( s ) + Δ M ( s ) Q ( s ) T(s)=1-S(s)=\frac{G_n(s)Q(s)}{G_n(s)+[G_p(s)-G_n(s)]Q(s)}=\frac{G_n(s)Q(s)}{G_n(s)+\Delta _M(s)Q(s)}T(s)=1−S(s)=Gn(s)+[Gp(s)−Gn(s)]Q(s)Gn(s)Q(s)=Gn(s)+ΔM(s)Q(s)Gn(s)Q(s)
有小增益定理,系统鲁棒稳定的充分必要条件:
∣ ∣ Δ M ( j w ) T ( j w ) ∣ ∣ ≤ 1 ||\Delta _M(jw)T(jw)||\leq1∣∣ΔM(jw)T(jw)∣∣≤1
通常情况下被控对象的不确定性随着频率提高而增大,即Δ M ( j w ) \Delta _M(jw)ΔM(jw)随着频率的增加而增大。在一般的运动控制系统工作频率范围,Δ M ( j w ) \Delta _M(jw)ΔM(jw)很小。此时T ( s ) ≈ Q ( s ) T(s)\approx Q(s)T(s)≈Q(s),近似为:
∣ ∣ Δ M ( j w ) Q ( j w ) ∣ ∣ ≤ 1 ||\Delta _M(jw)Q(jw)||\leq1∣∣ΔM(jw)Q(jw)∣∣≤1
截止频率设置越高系统抑制干扰能力越强,同时也导致补灵敏度函数在高频段具有较大的增益,干扰观测器的鲁棒稳定性变差。
参考
《面向实世界触觉通信的先进运动控制》