【LeetCode】【剑指offer】【二叉搜索树的后序遍历序列】

剑指 Offer 33. 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

     5
    / \
   2   6
  / \
 1   3
示例 1：

输入: [1,6,3,2,5]
输出: false
示例 2：

输入: [1,3,2,6,5]
输出: true

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

对于二叉搜索树，就是当前结点的左结点比当前结点小，当前结点的右结点比当前结点大，但是当前结点的右节点的最右下的结点又要比当前结点的父节点小。 

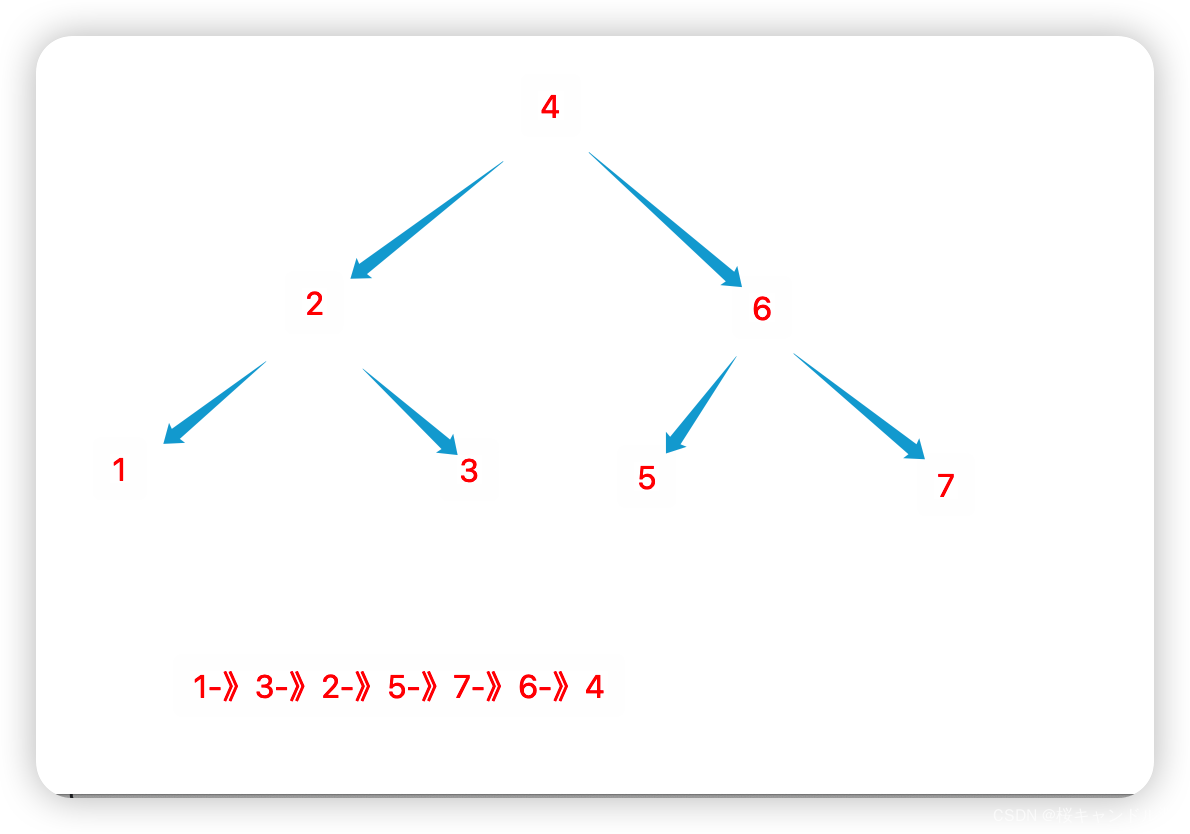
从上面这这表中我们可以看出我们的4是根节点，也处在我们后序遍历的最后一个位置。 

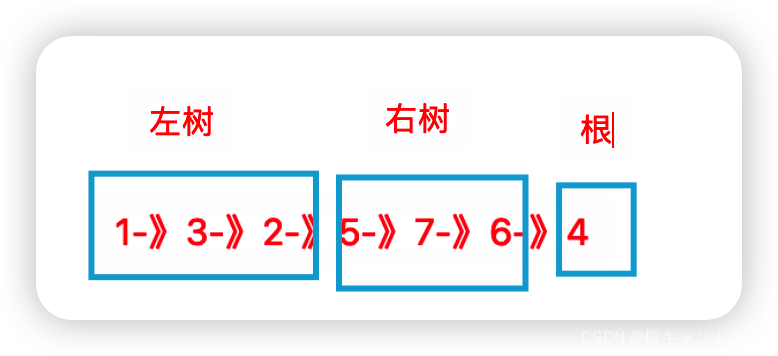
所以我们可以先读取当前后序遍历的最后一个数据作为我们的根结点，然后从前往后遍历我们的后序遍历容器，找到第一个大于根节点的数据，作为我们的mid，也就是说在这个数据之前的是我们根结点的左子树，在这个数据之后的是我们根节点的右子树。所以仿照上面的步骤，我们只需要递归遍历0到mid-1也就是我们的左子树区域和mid到end，也就是我们右子树的区域就可以得到我们最终的结果了。

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        return result(postorder,0,postorder.size()-1);
    }
    bool result(vector<int> & postorder,int begin,int end){
//begin>=end就是说明我们的子树已经查完了，所以返回TRUE
        if(begin>=end)
        {
            return true;
        }
        int pointer=0;
        while(postorder[pointer]<postorder[end])
        {
            pointer++;
        }
        int mid=pointer;
        while(postorder[pointer]>postorder[end])
        {
            pointer++;
        }
        return pointer==end &&result(postorder,begin,mid-1)&&result(postorder,mid,end-1);

    }
        
};