最小公倍数与最大公约数

如图所示

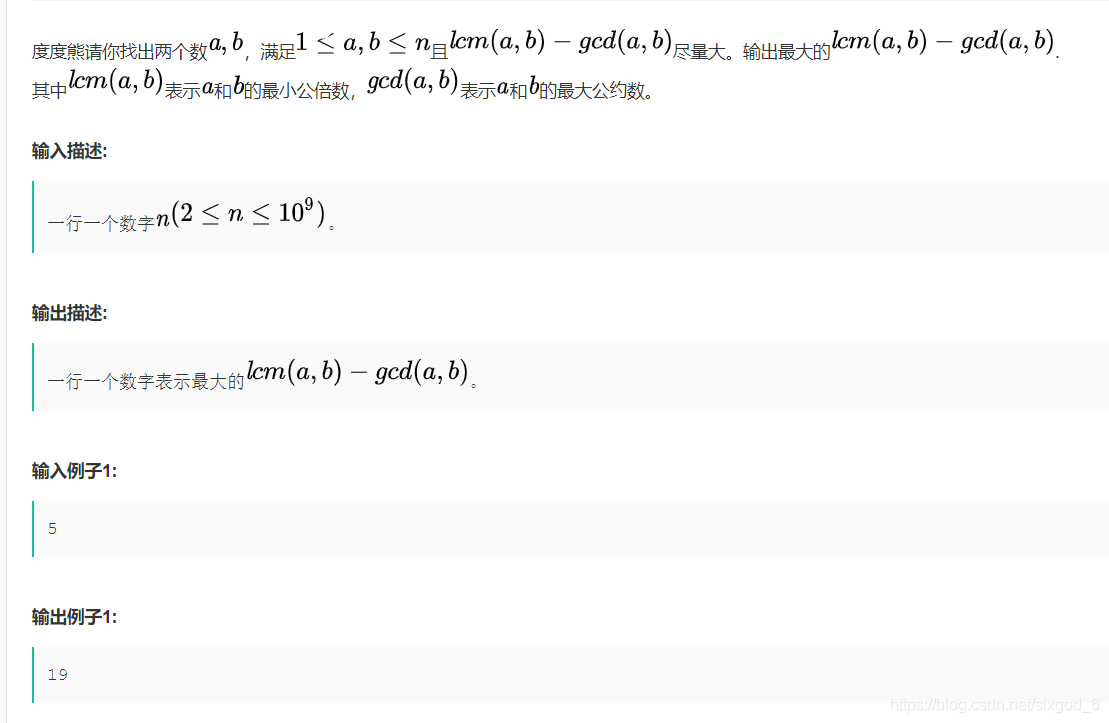
正确代码

#include <bits/stdc++.h>
using namespace std;

int main(int argc, const char * argv[]) {

  long len;//注意此处的long型接收输入数值
  cin>>len;
  if(len==1) cout<<0<<endl;
  else cout<<len*(len-1)-1<<endl;

      
  return 0;
}

lcm最小公倍数是两数相乘除以最大公约数，
gcd最大公约数可通过

//1.辗转相除法
#include <stdio.h> 
int main()
{
	int a,b,c;
	scanf("%d%d",&a,&b);
	while(b)
	{
		c=a%b;
		a=b;
		b=c;
	}
	printf("%d\n",a);
	return 0;
}

//2.更相减损术

#include <stdio.h> 
int main()
{
	int a,b;
	while(scanf("%d%d",&a,&b)!=EOF)
	{
		while(a!=b)
		{
			if(a>b)
				a=a-b;
			else
				b=b-a;
			
		}
		printf("%d\n",a);
	}
	return 0;
}

但需要重点强调的是，本题中由于求最小公倍数与最大公约数差的最大值，我们可以分析：

n与n-1之间一定只存在最大公约数为1，而n与n-1之积为最大，所以可以直接返回n*(n-1)-1

但此类型题重点关注的不是解法，而是输入用例的范围测试。
如题所示：

$$2\le n\le 10^9$$

这么大的数值，只用int是无法接收的，int能表示的最大值为：

0111 1111 1111 1111 1111 1111 1111 1111 (最高位表示符号位，正数符号位为0)对应的10进制数为2^31-1=2147483647，对应的十六进制表示为：0x7FFFFFFF。

很明显，此处需要用长整型long处理。

还原数列

正确代码

#include <bits/stdc++.h>
using namespace std;

int main(int argc, const char * argv[]) {

  long b;
  long n;
  cin>>n;
  long data[n];
  for (int i = 0; i < n; i++)
  {
    cin>>b;
   data[i]=b;
  }
  sort(data,data+n);
  long k =0;
  int temp = 0;
  while (data[n-1]>=n)
  {

    
    temp =(long)(data[n-1]/n);
    k=k+temp;
    for (int i = 0; i < n-1; i++)
    {
     data[i]=data[i]+temp;
    }
    data[n-1]=data[n-1]%n;
     sort(data,data+n);
    temp = 0;
  }
  cout<<k<<endl;
  
  return 0;
}

本题与上面例题一致，强调的仍然是测试用例的范围：

$$1\le a[i]\le 10^{18}$$

所以我们仍然需要用long型接收输入数值。

解题逻辑不难，每次sort排序数组，取最大值data[n-1]减去题中要求的n值，用data[n-1]/n判断该最大值需要减几次，最后给所有其余数加上这个次数，完成data[n-1]<n，最后循环处理所有数据即可。

一定要注意测试用例的输入范围

如果笔试中真遇到这种题，想必很多人是懵逼的，就算最后发现问题所在，时间也会耽误很多，最好的就是在练习中积累经验。总之，多写题。