Lec01,
线性代数基础,
to solve a system of linear equations求解线性方程组
n equations , n unknowns
Row picture-- the picture of one equation at a time
*Column picture
2 equations ,2 unknowns

列向量的线性组合(linear combination)
所有的线性组合,结果是?这两个向量的组合会布满整个坐标平面
what linear combination gives b? what do all the linear combinations give?
3 equations , 3 unknowns
3维,线性方程 的所有解构成一个平面 ,3点确定一个平面
3x3问题的每一行都是三维空间的一个平面
三个平面相交于一点
消元法elimination ,求解的系统方法,how to find x,y,z in all cases.(计算机程序都用该法)
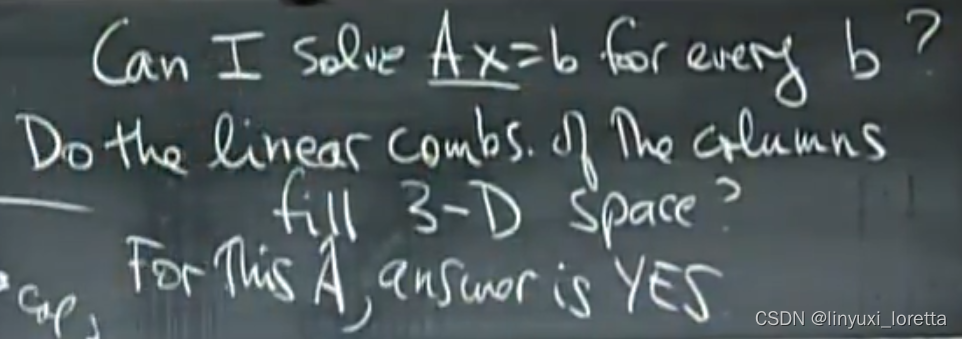
非奇异矩阵a non-singular matrix、可逆矩阵an invertible matrix,任何b都有解
如果三个列向量同处一个平面,列向量相互不独立,奇异矩阵、不可逆矩阵
矩阵 乘以 向量,方法1:一次一列,列的线性组合; 放法:一次一行 *向量,点乘dot product
Lec02,
消元法 求解任意元的方程组; 什么情况下,方程组无解
消元只是行变换row operations ,
Gauss高斯
消元过程:
“pivot” 主元,不能为0
matlab先算完左侧矩阵,然后再回头算右侧向量
(2,1)step---(3,1)step--(3,2)step
upper triangular上三角矩阵(U) ,消元的目的是从A得到U,
行交换可以解决主元为0的“暂时性失效”,
“回代”substitution “增广矩阵”augmented matrix

消元矩阵elimination matrices(E)
1 0 0
0 1 0
0 0 1
identity matrix 单位矩阵(I)
矩阵乘法的性质:
结合律(移动括号)associative law,the orders of matrices 不能改变
初等矩阵elementary matrix
交换两行,置换矩阵permutation matrix(P)
在左边用矩阵做乘法、进行的是行变换row operation,
在右边,列变换
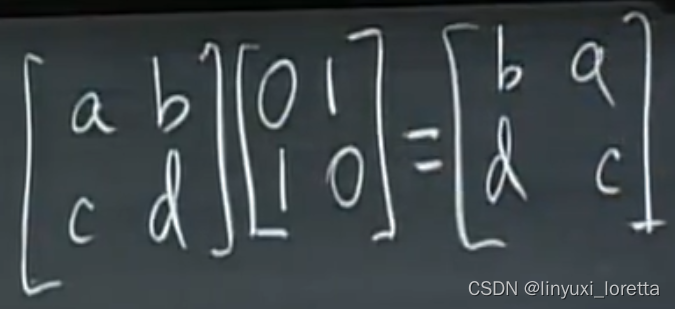
逆矩阵,
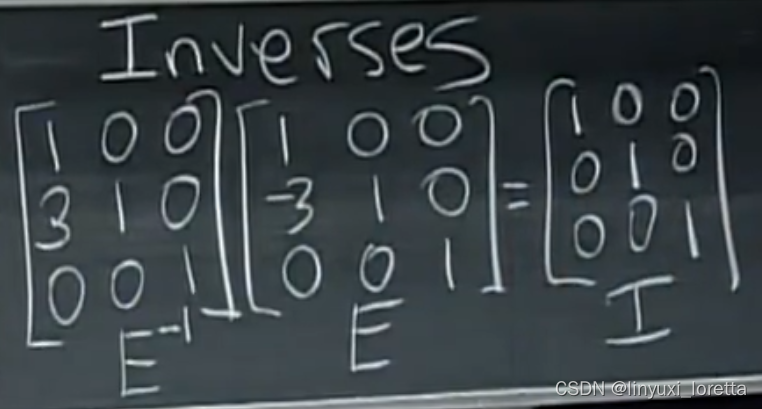
find the matrix ----which undoes elimination取消这次消元
Lec03,
矩阵乘法四种方法:
1. 点乘
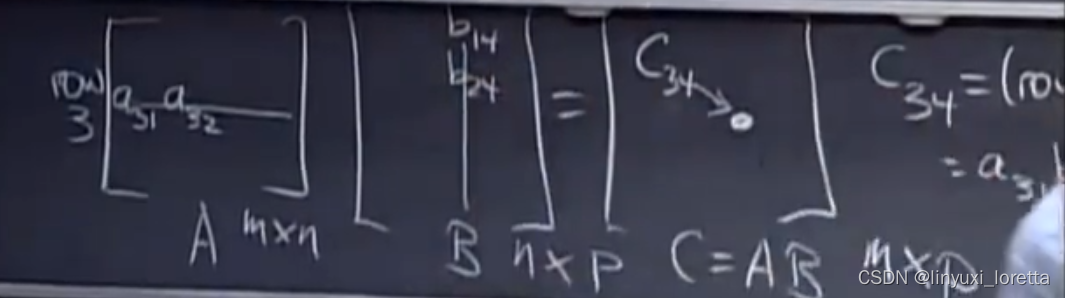
2.列方法
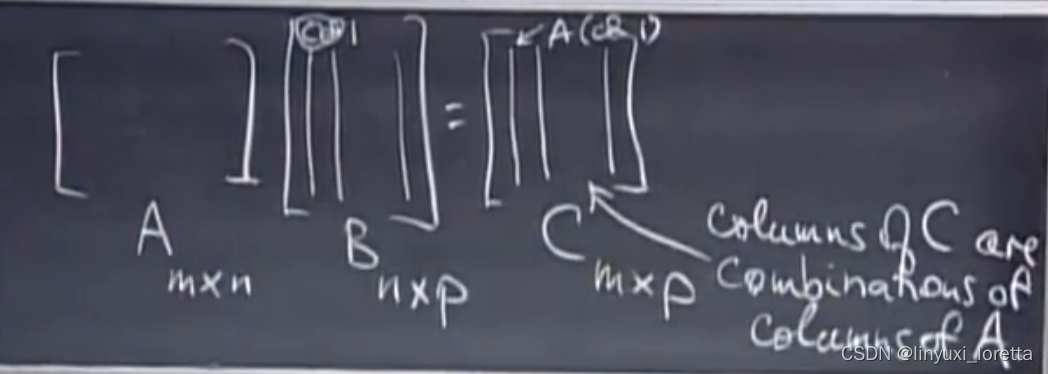 3.行方法
3.行方法
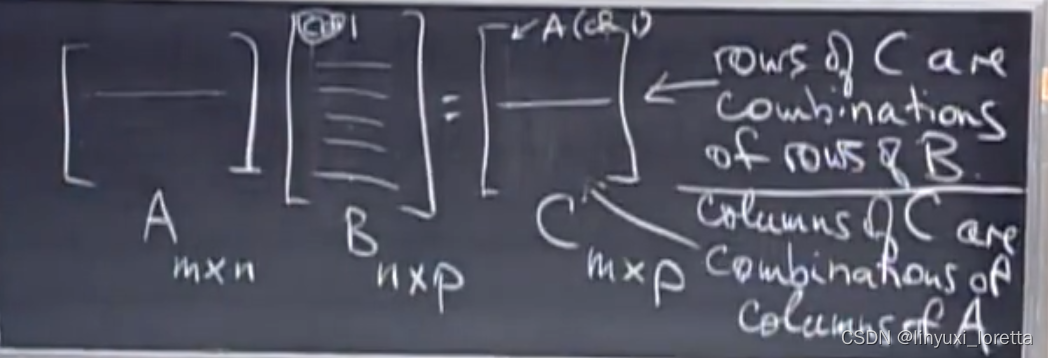
4.
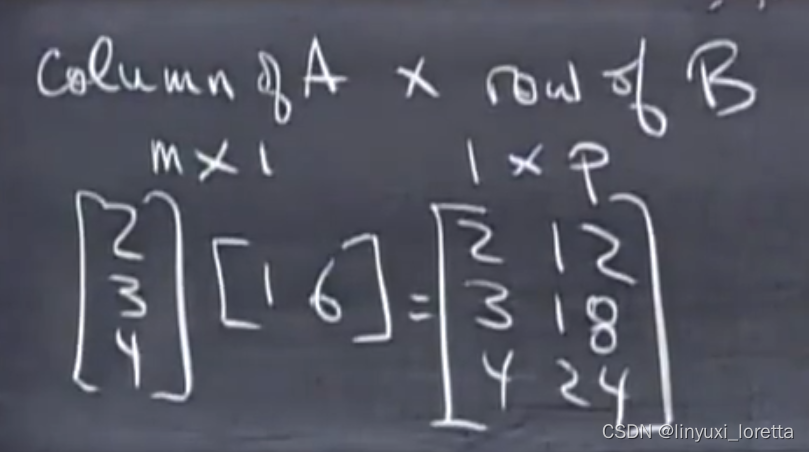
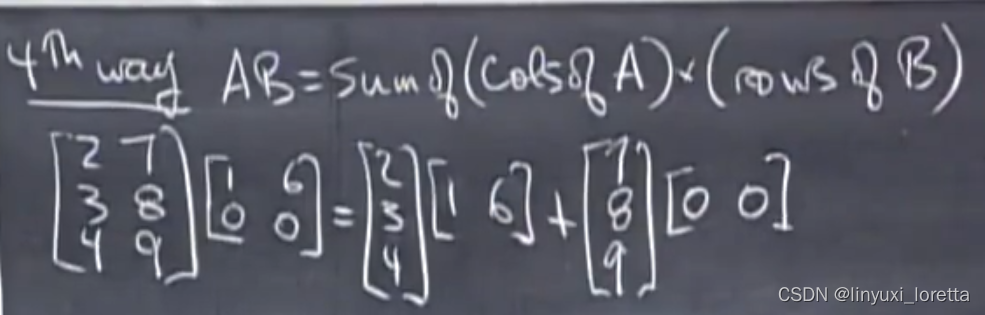
所有行依赖于同一行,如果画向量,他们都是同一方向,
画出列向量,也会是一个方向
该矩阵 行空间和列空间 都是一条直线,
行空间row space:行所有可能的线性组合
分块乘法

逆inverses (square matrices)
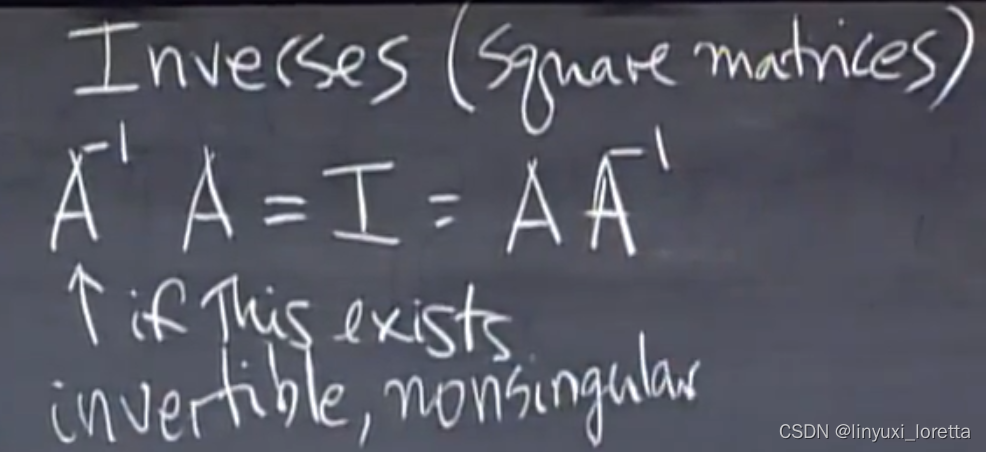
逆 不存在的判断条件:
1.行列式=0
2.A中两列共线,所有的线性组合均在此直线上,1 0却不在
3.存在向量X,AX = 0,

如果其中一列对线性组合毫无贡献,矩阵不可能有逆
Gauss-Jordan 一次求解2个方程组 、求逆。 先向下操作,再向上操作
对左边 消元--->单元阵,右边则变成逆矩阵
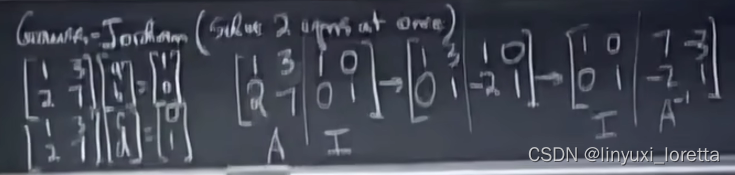
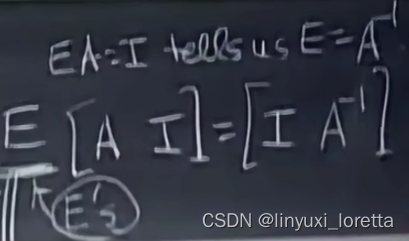
Lec04
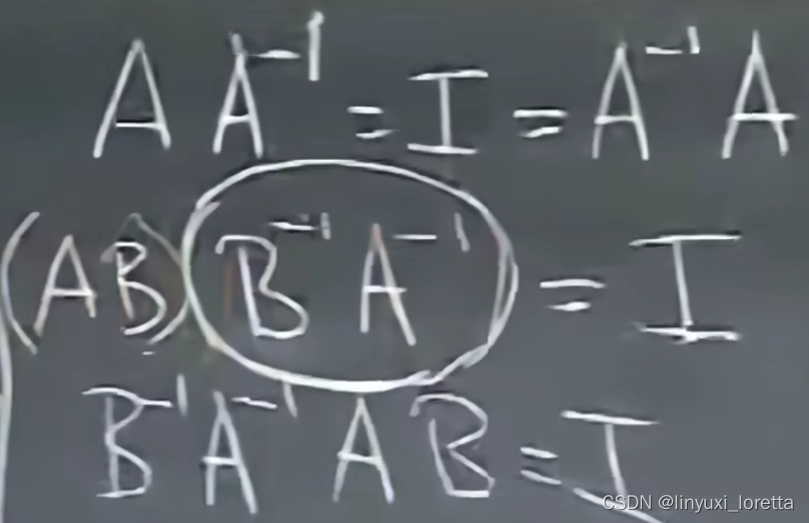
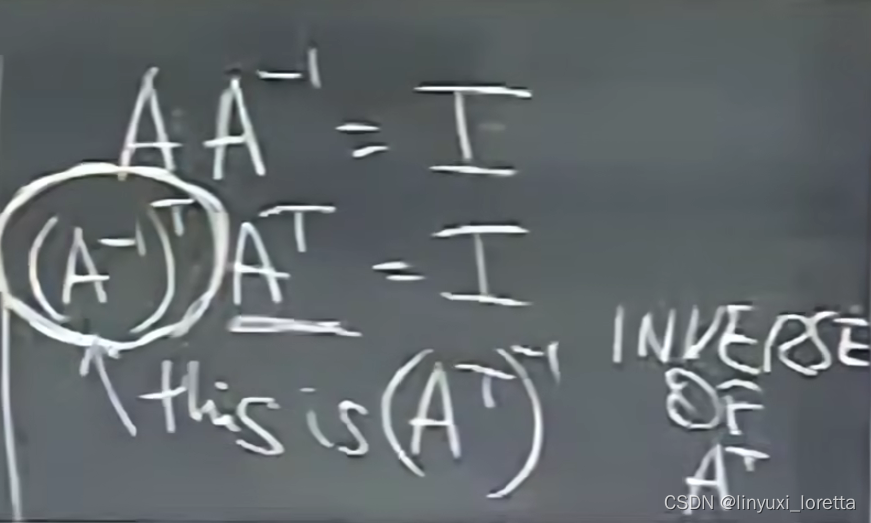
可逆方阵的转置 transpose
单位阵(I) 对称,转置不变
转置:行和列互换, 交换对角线两端元素
对于单个矩阵,转置和逆两种运算,顺序可以颠倒
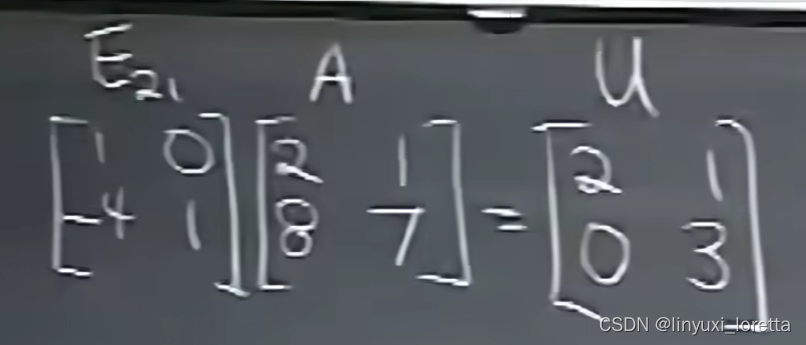
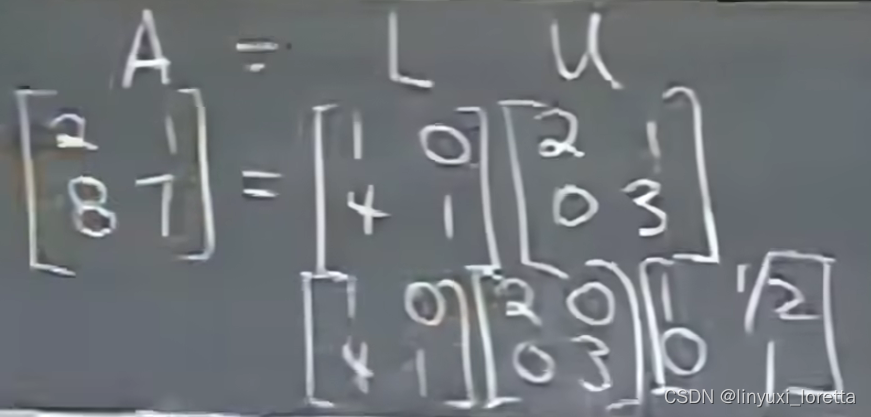
A=LU 是最基础的矩阵分解
L 下三角矩阵lower ,对角线元素均为1
有时,将主元单独列出来,对角矩阵diagonal matrix
这里教授应该是按行的线形组合推出第三个矩阵,其实也可以按列推
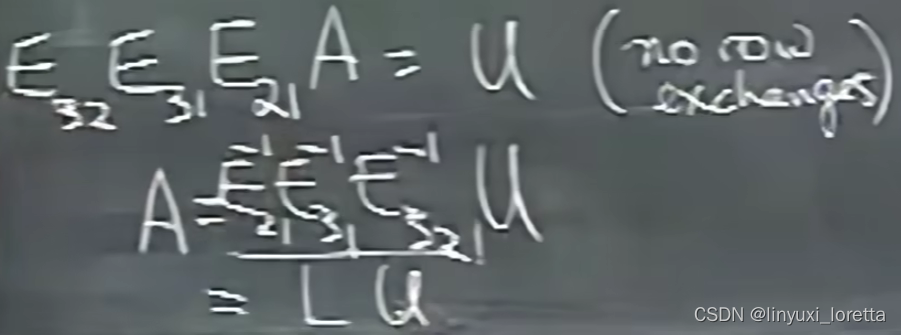
为什么要用逆的形式?下面的积比上面的积好
举例:
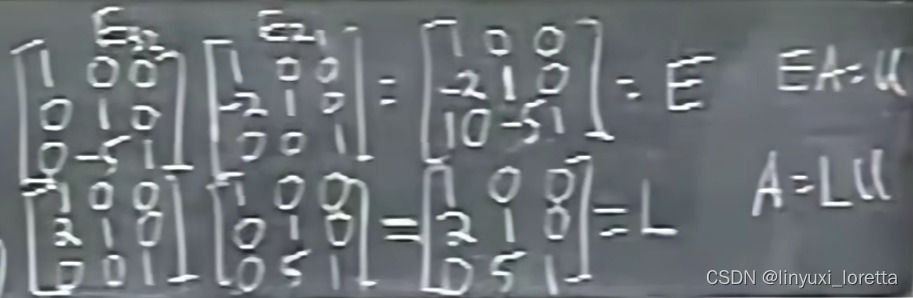
L中矩阵相乘的顺序非常好,消元乘数还在L里,要求出L,不需要任何运算,只需要把所有消元乘数都写进来:
A= LU
if no row exchanges,
消元乘数 multipliers go directly into L
How many operations on n x n matrix A? (operation = multiply + sustract )
算法复杂度O(n²),不是准确的次数
因为这里是对于每一行都进行一次消元,一次消元就要对第一行的N个数乘上一个常数,再用该行减去,一共有N-1行,因此就是N*(N-1)
COUNT: n^2+(n-1)^2+...+1^2 ≈ 1/3n^3
行列式 是 n的阶乘,
但是不连续啊,求和的并不是从n方到1的连续值,而是离散值
对x^2积分,得到1/3x^3
cost of b:n^2
转置与置换 transpose & permutation
A33,排列组合 =3!= 6
不管怎么相乘,结果始终仍在它们之中,他们的逆也仍在群中

置换矩阵奇妙的性质:其逆= 其置换

matlab检验主元位置,且不允许存在主元接近0,对数值准确性有影响,
对称矩阵symmetric matrices
转置后形态不变
对角线上元素任取、其他行和列中元素必须对应,
rectangular长方阵 (R),R*R转置 永远是 对称矩阵
why?take transpose!这是验证对称性的不二法门
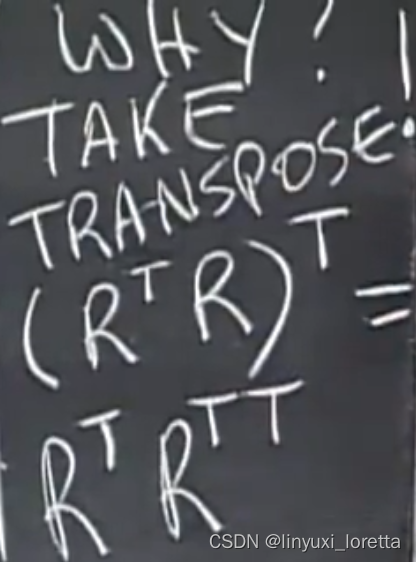
向量空间vector space 子空间sub-spaces
加法、数乘

e.g. 已知v,可求3v
已知v、w,可求v+w
空间,表示有很多向量,一整个空间的向量
空间必须能进行加法和数乘运算,必须能进行线性组合,
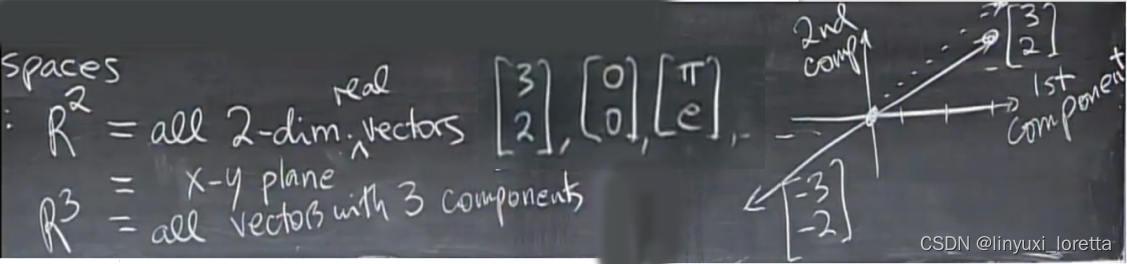
水平表示第一个分量,竖直表示第二个分量




line meaning infinitely far in both directions through the zero
和R1相比,都是直线,但在情况2中,向量都有两个分量,因此他们截然不同

how do the subspaces come out of matrices?
从矩阵中构造出一个子空间
通过列向量构造,列空间 C(A) column


让我们能从更高的层面审视 线性代数,如何用向量空间和列空间,理解Ax=b(Lec06)
Lec06. 列空间和零空间
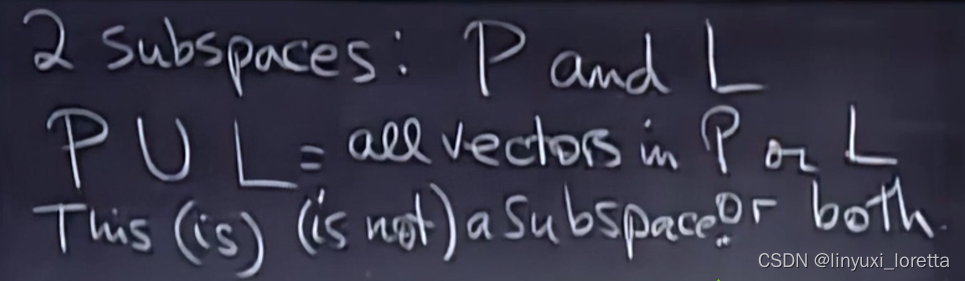
NO。

如果取两个向量、他们同时属于两个子空间、这相当于一个更小的向量集合,因为条件增加了
向量空间必须满足的两个条件:加法封闭和数乘封闭
三个向量构不成vector space,怎样将其扩充为subspace?取线性组合即可
下面,把他同线性方程组联系起来
Ax=b对任意b总有解?NO。 因为4 方程、3未知数。3个列向量的线性组合无法充满整个四维空间
怎样的b能让方程组有解??
1.zero vector
2. 右侧向量很特殊,等于A中某列
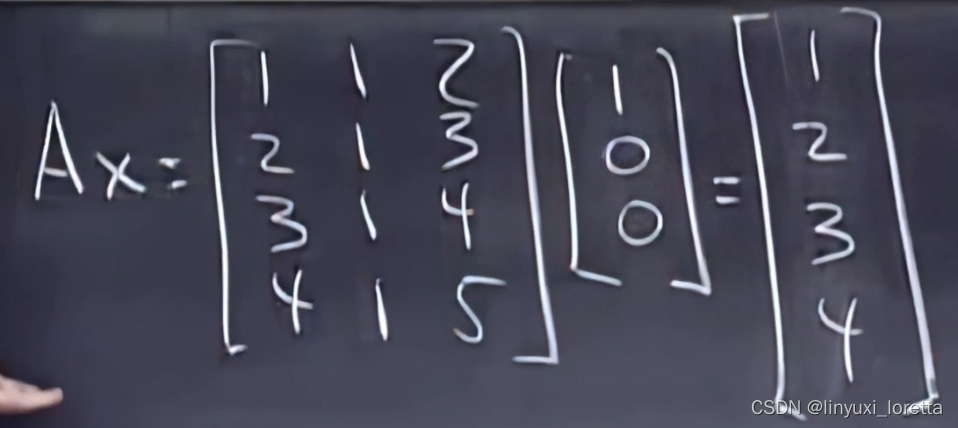
Ax=b有解,当且仅当右侧向量b属于A的列空间(in R^4)----b是各列的线性组合
are those 3 columns independent?这三列线性无关吗?
= 是否每列都对组合有所贡献 ?
= 我能否去掉某列,得到同样的列空间?
列3等于前两列之和,处于前两列的平面上, 所以这两列被称为“主列”pivot columns,去掉列一也一样可以,只是习惯优先考虑考前的线性无关向量
零空间null space
它不包含右侧向量b,
它包含all solutions x,to Ax =0 .(此时b=0) in 三维空间R^3
求零空间和列空间的一般方法:消元法
关心线性组合的系数
零空间是R^3中的直线
why零空间是向量空间? 证明:加法、数乘

除0以外的b,如果有解的话,他们构成子空间吗?现在需要考虑R^3中所有满足Ax=b的解,所有解x构成向量空间吗?
因为0向量不是方程组的解,不是向量空间。
是一个不穿过原点的平面或直线, 本例是一条不穿过原点的直线
总结:两种方法构筑子空间
从几个向量,通过线性组合,得到子空间
从一个方程组,通过让x满足特定条件来得到子空间
如何找出这些空间中的向量,如何计算出这些向量
求解AX=0的算法,长方阵, 有线性相关项---->消元 ,长方阵 哪怕主元位置是0 ,仍得继续
目标:消元过程中,方程组的解不变,零空间不会改变

echelon form阶梯形式
秩rank of the matrix = number of pivots
pivot variables主变量
求解AX=0
1. do elimination
2. 确定主列和自由列,r,n-r
3. 对自由变量分配数值,通常令其中一个为1 ,其他为0
4.回代
特解special solutions,每个自由变量对应一个特解
m x n矩阵,m rows、n columns,n变量,
r=2,r个主变量,表示只有r个方程起作用
n-r 自由变量,
简化行阶梯形式reduced row echelon form( matlab rref(A)命令 )
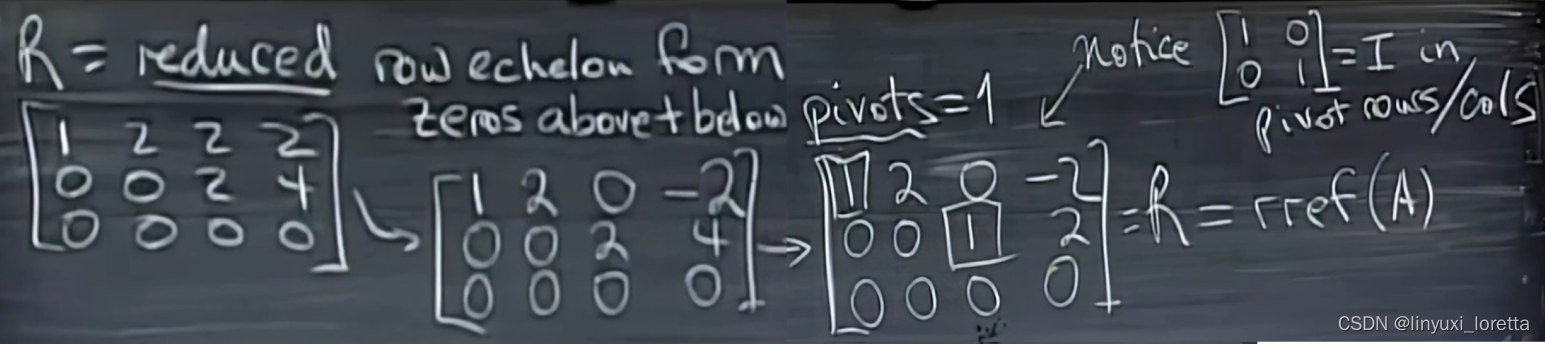
他以最简形式包含了所有信息:
主行:行一和行二;主列:列一和列三
单位阵I 处于主行和主列交汇处
自由行,全是0的行表示:这行是其他行的线性组合
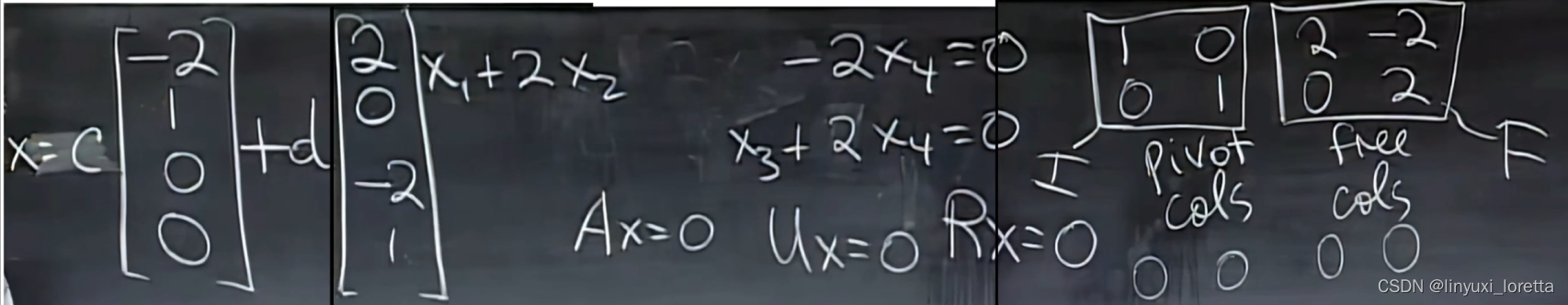
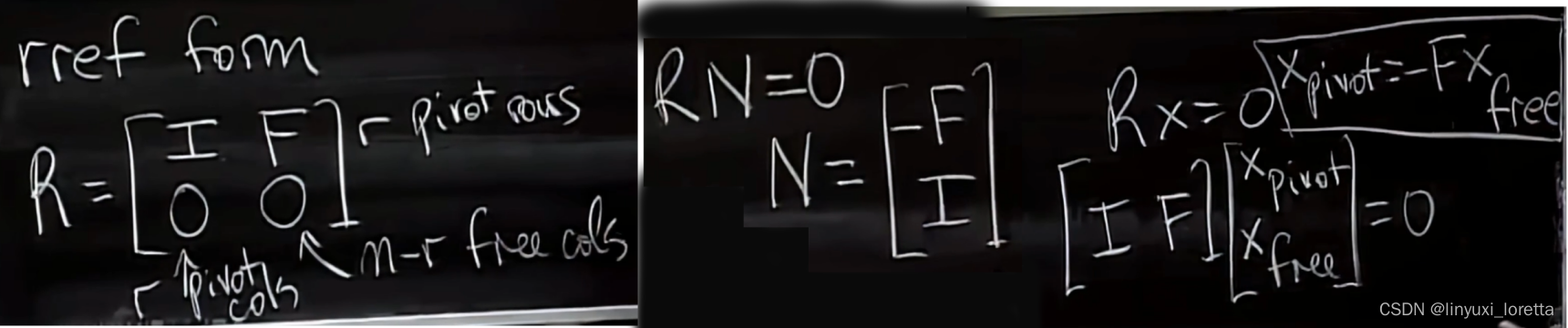
null space matrix零空间矩阵,
matlab可以通过null(A)指令、生成null basis零基、零空间矩阵
RX=0
e.g.2
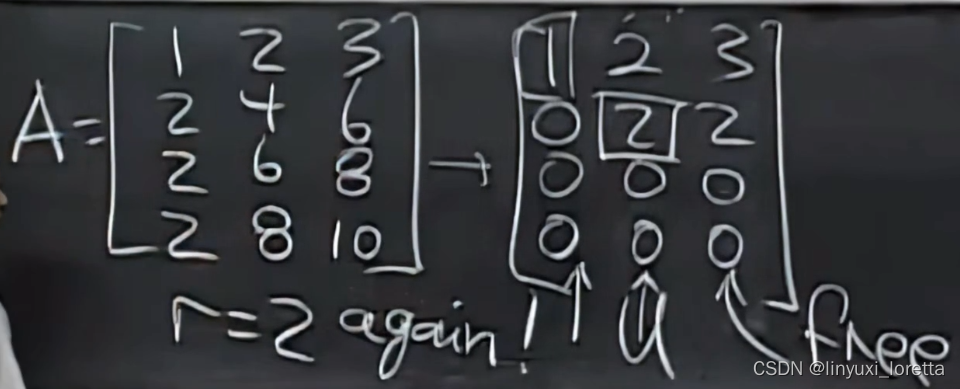
零空间呢?矩阵的特解有几个?主变量、自由变量?
矩阵A主列的个数 和A转置相同
自由列:3-2=1
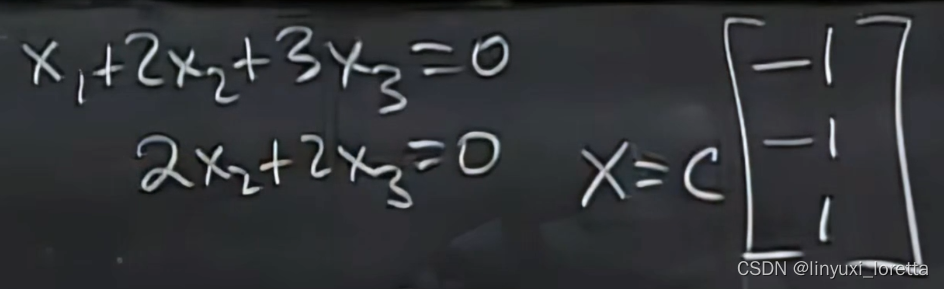
零空间的基basis for the null space
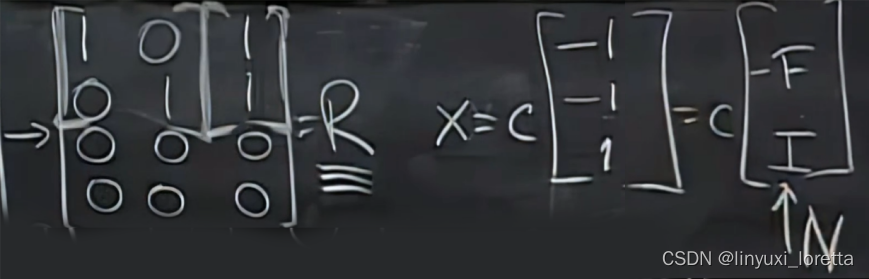
null space matrix零空间矩阵,各列由特解组成
因此其自由变量部分为 I、主变量部分为-F、
so do you see , though, how the -F just automatically shows up in the special solutions.
Ax = b
Ax=0 齐次方程组、称为 Ax = b 的“导出组”

有解的条件condition forsolvability:0 = b3-b2-b1
方程有解的条件?

求解过程:
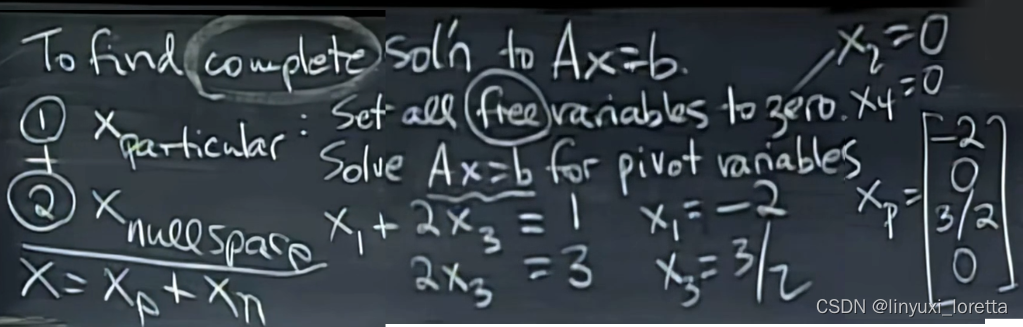
1.保证0=0,so 最后一个方程ok
2.令所有自由变量为0,解出主变量
得到特解
所有解怎么求:特解+零空间中的任意x
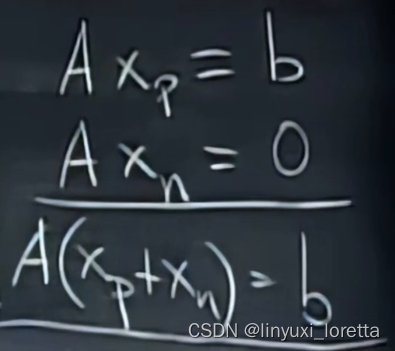
教授将Ax=b特解表示为particular solution特定解;Ax=0基为special solution特殊解
零空间包含所有特殊解的线性组合,两个特殊解、因为有两个自由变量

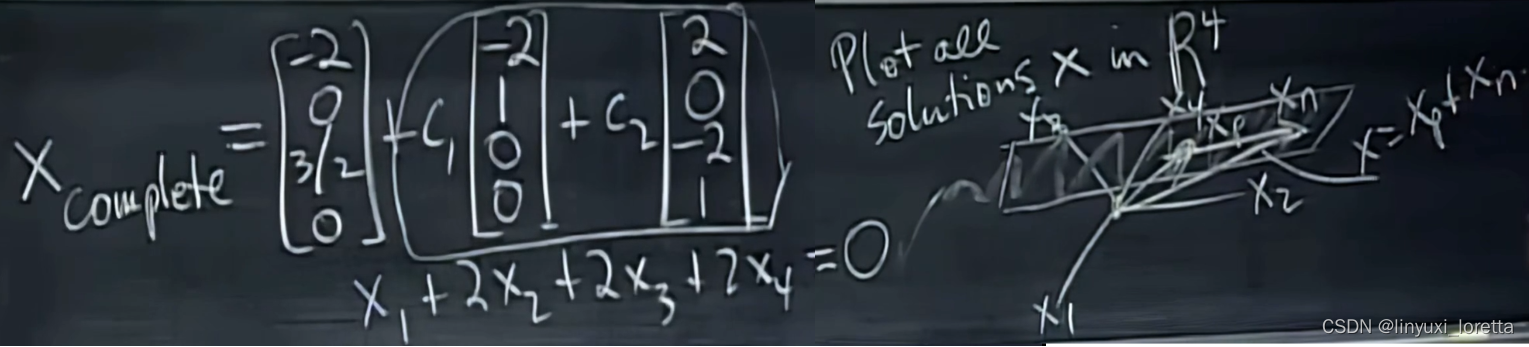
Ax=b的解是一个平面,但不包含0点
算法:
消元-->求出particular solution,--->求special solutions(基础解系)
推广:m rows、n columns
情况1. e.g. 列满秩
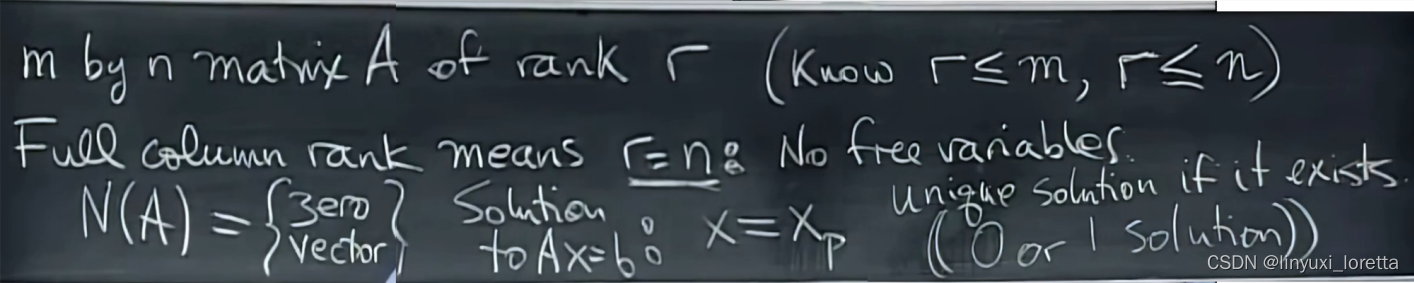

消元后得到多少主元?两列向量的方向不同、
是否Ax=b总有解?4方程2未知数,一般情况都无解、只有b是各列的线性组合时,
情况2. 有列多余、行满秩
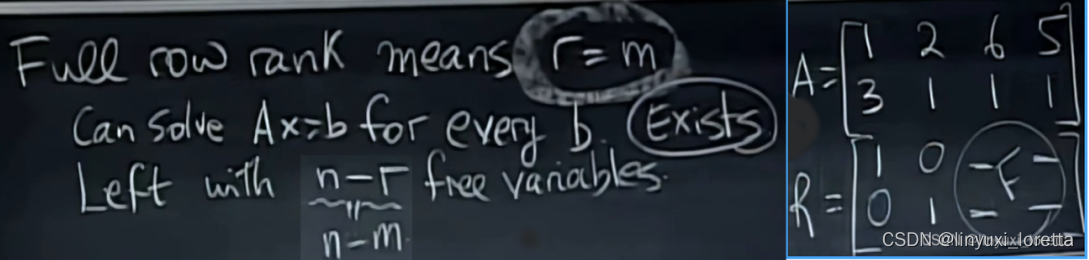
消元时不会出现零行, 因此b没有要求、
F表示各自由列(free),这部分将构成零空间的特殊解、
情况3。可逆方阵(Ch.2)
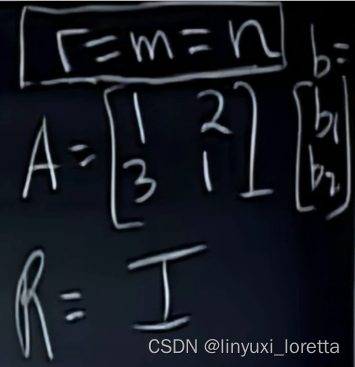
rref:R=I
零空间只包含0向量
Ax=b有解,b的条件,不需要、任意b都有解
又由于r=n,解唯一
情况4.r<m,r<n
无解,因为we didn't get a zero equals zero for some Bs
或无穷多解、
本章总结:
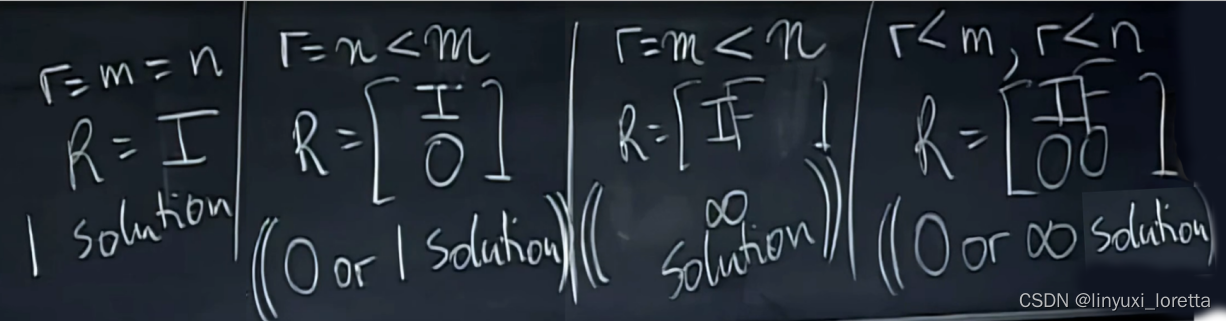
矩阵的秩决定了方程组解的数目
行列式 determinants = 主元之积