方阵函数的计算一般有两种方式:Jordan标准型法和最小多项式法。
一、Jordan标准型法
假设存在矩阵A,有.我们已知存在
.也就是若对矩阵A函数计算,可以通过先对它的相似Jordan标准型J进行相同函数计算,之后左乘变换矩阵
,右乘变换矩阵
得到需要的结果。
这是因为对于Jordan标准型而言,函数计算存在以下方便的计算方法:

也就是对Jordan标准型矩阵的计算可以转换为对对角元λ的代数计算,矩阵计算变代数计算,显然简化了许多。之后再左乘变换矩阵,右乘变换矩阵
得到需要的结果。
例题:有矩阵A=,求f(A)
解:①先通过,求解其特征值λ1,λ2=λ3,……(注意,这里边一般存在重根,若不存在重根那就意味着可以直接相似为对角阵,那样比Jordan标准型更简单了)。
②针对不同特征值求解其特征向量,一般对于重根会出现几何重数小于代数重数,意味着只能相似为Jordan标准型,求出其Jordan标准型,(具体求法在前面中讨论过)。
③针对Jordan标准型按照上图方法求出其结果(切记对不同Jordan块都得求出,别忘记了)
④ 按照求出f(A)的值即可。
该方法计算难点:
- 相似变换矩阵
及其逆矩阵
难求
- 3个矩阵相乘
计算繁琐。
二、最小多项式法

注意:(1)满足条件里f(λ)中的λ为方阵A的特征值。
(2)f(λ)求导的次数为相应特征值代数重数减1
(为什么是中
减1呢,其实是为了构造下面所示的Jordan块函数相等,已用红色标注出来,太巧妙了。
为什么要用最小多项式作为已知首选条件呢,这是因为:最小多项式中中
的大小限制了针对
子Jordan矩阵
中Jordan块
的最高阶
)
由定义1的条件可以看出,


这是因为![]()
由此,可知计算方阵A的f(A)函数的另一种方法是构建一个多项式g(λ)与f(λ)在方阵A上谱一致就可以,这样将f(A)计算转化为了g(A)的计算。
计算方法:


之后将f(A)计算转化为了g(A)的计算。
例题:有矩阵A= ,求f(A)
①求A的特征多项式,由特征多项式求出其最小多项式。(与其说是求出不如说是试出最小多项式)
②针对最小多项式构造一个多项式:
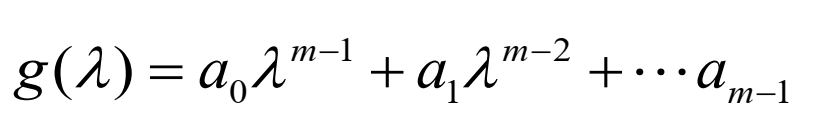
注意上面的最高次数为m-1,m为最小多项式的所有指数和。
根据

求出a0,a1,a2……an,带入g(λ)函数中,之后将方阵A带入g(λ)函数中求解。
总结:运用泰勒展开方法计算方阵函数,由于收敛域会缩小函数的范围,存在不可计算的现象,运用Jordan标准型或最小多项式法计算方阵函数可以有效避免。
(非常感谢杨教授的网课,受益匪浅!!!)