分治法的算法思想:把原问题分成k个较小规模的子问题,对这k个子问题分别求解。如果子问题不够小,那么把每个子问题再划分为规模更小的子问题,直到问题足够小,就很容易求出这些子问题的解,从而求出整个问题的解。
由于分治法的思想与递归的过程几乎一样,所以用递归来实现分治法是理所应当的。
下面介绍两种体现分治法思想的算法:
1.快速排序的二分优化
快速排序是基础的算法,如果不了解快速排序的小伙伴可以去搜索快速排序,有关快速排序的算法网上的资源非常的多。在这里主要是分享一下在实际刷题过程中遇到快排的题,基本上都可以拿二分优化AC。
<1.>为什么要进行二分优化:因为快速排序不稳定,快速排序的模板只是以数列中的第一个或最后一个数为基准数,那么当数列全按降序排列而要求你进行升序排列的时候时间复杂度就会为O(n^2),在做题的时候,当数据规模较大的时候往往会运行超时,要想使得快排的效率稳定就必须对其进行优化。
<2.>算法思路:与二分法的思路一样,选取区间的中点作为基准数,然后进行快排,让i从区间的左边出发,j从区间的右边出发,在i<=j的条件下,进行搜寻,一轮排序的过程跟基础快排一样。但是一轮排序后的结尾需要注意,由于i,j都可能指向中间的基准数进行交换,所以结束的时候,j势必会在i的前面,所以我们再次分配区间的时候就以i,j所在的位置进行左右区间的划分。这样做的好处就是不会出现每次基准数都是区间两端的数,从而使得最坏的情况得到优化,使算法的最坏复杂度趋近O(n*logn)。
以此题为例:
题目描述
利用快速排序算法将读入的 N个数从小到大排序后输出。
输入格式
第 1 行为一个正整数 N,第 2行包含 N 个空格隔开的正整数ai ,为你需要进行排序的数,数据保证了 Ai 不超过 10^9。
输出格式
将给定的 N个数从小到大输出,数之间空格隔开,行末换行且无空格。
输入输出样例
输入 #1复制
5 4 2 4 5 1
输出 #1复制
1 2 4 4 5
说明/提示
对于 20% 的数据,有 N ≤10^3;
对于 100% 的数据,有 N ≤10^5。
代码如下:
``
#include<bits/stdc++.h>
using namespace std;
int n;
int a[100005];
void quicksort(int l ,int r){
int mid = a[(l+r)/2]; //注意这里一定是mid = a[(l+r)/2],不能是mid = (l+r)/2;请读者自己思考原因
int i = l,j = r;
do{
while(a[i]<mid) i++; //注意a[i]<mid,不是<=,保证mid能被交换
while(a[j]>mid) j--;
if(i<=j){
swap(a[i],a[j]); //交换a[i],a[j]
i++;
j--;
}
}while(i<=j);
// cout<<"("<<l<<","<<r<<")"; //打印区间
// for(int k = l;k<=r;k++){ //可以打印排序过程,有助于理解排序过程
// cout<<a[k]<<" ";
// }
if(l<j) quicksort(l,j);
if(i<r) quicksort(i,r);
}
int main(){
cin>>n;
for(int i = 1;i<=n;i++)
scanf("%d",&a[i]);
quicksort(1,n);
for(int i = 1;i<=n;i++)
cout<<a[i]<<" ";
return 0;
} 衍生问题:求第K小的数
值得一提的是,由快排衍生出的求第K小的数的问题,因为快排是根据划分左右区间来进行的,所以很容易想到解决此题的办法,在每一轮排序结束后,让i,j和K比较,如果k>=i则对右区间进行排序,如果k<=j则对左区间进行排序,从而快速的求出第K个较小的数。
要求解此题,我们只需要更改部分代码即可:
将
``
if(l<j) quicksort(l,j); if(i<r) quicksort(i,r);
改为:
``
if(k<=j) quicksort(l,j); //
if(k>=i) quicksort(i,r);
else{
cout<<a[j+1];
exit(0);
}因为最后递归的子区间是(k,k),所以j会向左移动到k-1处,这是第K个元素已经完成排序,输出a[j+1]即可。
归并排序(逆序对问题)
逆序对:对于给定的一段正整数序列,逆序对就是序列中 ai>aj 且 i<j的有序对。例如5 4 1 3 2序列中,就存在(5,4),(5,1),(5,3),(5,2),(4,1),(4,3),(4,2),(3,2)这些逆序对。
以此题为例:
传送门:逆序对 - 洛谷
看完题目,想必小伙伴们脑海中已经有思路了,没错就是暴力啦~虽然暴力很好实现但是O(n^2)的复杂度,让作为一个优秀程序员的你是不是有些头疼呢~之所以要学习算法就是要降低程序的复杂度,所以在这里为大家介绍求解逆序对问题的归并排序算法。与快速排序的基本算法思想一样,都是分治法,划分左右区间进行递归。归并排序比快速排序稳定哟~
算法思路:
1.分解:把初始序列分成长度相同的左、右子序列,然后把每个子序列在分为更小的子序列,直到子序列只包含一个数,程序由递归实现,因此可以把此情况看成递归的最底层。
2.排序-合并:将左右子区间的数按照升序进行排列,这时我们需要一个辅助数组b[n],当一个区间里面的数小于另一个区间里的数时,就将小的数放到辅助数组中,当左、右子区间里的任意一个区间没有数可排的时候,将对未处理完的区间里的数之间放到b[n]中去。为什么能够直接将未处理完的区间直接进行复制?因为是从单个数向上处理的,所以任意子区间的数按照处理规则已经排序完毕,所以除最底层外任何区间内都是有序的,所以再将两个子区间进行合并时可以直接copy未处理完的子区间。
处理过程如下图:
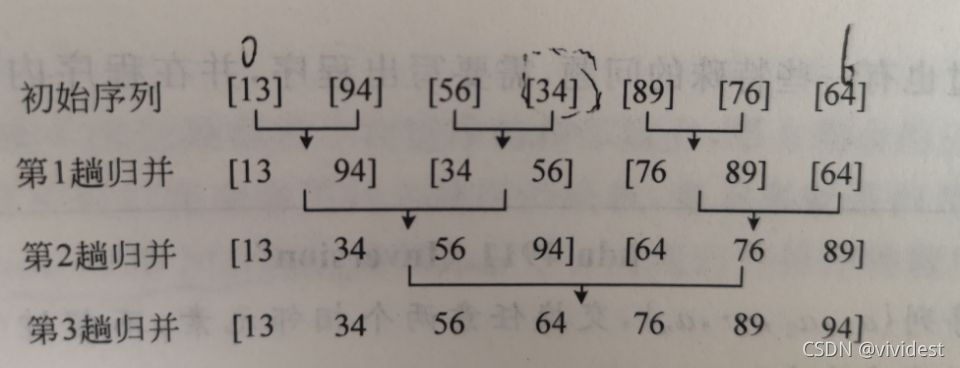
逆序对的产生:在归并过程中如果右区间的数小于左区间的数,是不是就是一个逆序对呢?所以在归并过程中,统计这样的情况之和就是逆序对的个数。例如:左区间[5,6,7]下标为i,右区间[1,2,9]下标为j,当 j= 1时逆序对为(5,1)(6,1)(7,1),当右区间产生逆序对时每个数会产生mid - i+1 个逆序对,即从i到mid个逆序对,所以每次需要累加mid - i + 1。
上代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[500005],b[500005];
long long ans = 0;
void gbsort(int l,int r){
if(l==r) return ; //跳出条件
int mid = (l+r)/2,i = l,k = l,j = mid+1;
gbsort(l,mid);gbsort(mid+1,r); //划分左右子区间
while(i<=mid&&j<=r){ //处理左右区间,排序-合并
if(a[i]<=a[j])
b[k++] = a[i++];
else{
b[k++] = a[j++]; //产生了逆序对,答案累加mid-i+1
ans += mid-i+1;
}
}
while(i<=mid) b[k++] = a[i++]; //copy余下子区间,完成合并
while(j<=r) b[k++] = a[j++];
for(int q = l;q<=r;q++) //将排好序的数组b[],复制回a[]中
a[q] = b[q];
}
int main(){
cin>>n;
for(int i = 1;i<=n;i++)
scanf("%d",&a[i]);
gbsort(1,n);
cout<<ans;
return 0;
}
如果想进一步的了解逆序对的相关问题,也有传送门鸭~(●'◡'●):
欢迎留言~
(觉得不错的小伙伴们点个赞再走吧~球球了)