Python PyTorch5：交叉熵、对抗过拟合

1. 交叉熵

对于以下二次代价函数：

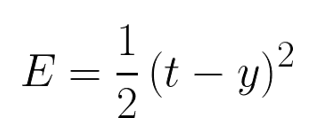t表示真实标签，y表示网络的预测值。

对其求导：

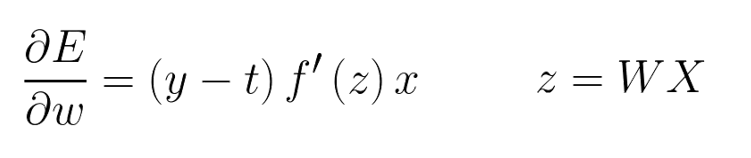W是权值，X为网络的输入。

f’(z)与w相关。激活函数的梯度f’(z)越大，w的大小调整得越快，训练收敛得就越快。激活函数的梯度f’(z)越小，w的大小调整得越慢，训练收敛得就越慢。

以一个二分类问题为例，进行两组实验。输入同一个样本数据x=1.0，该样本对应 的分类为y=0，使用sigmoid激活函数。

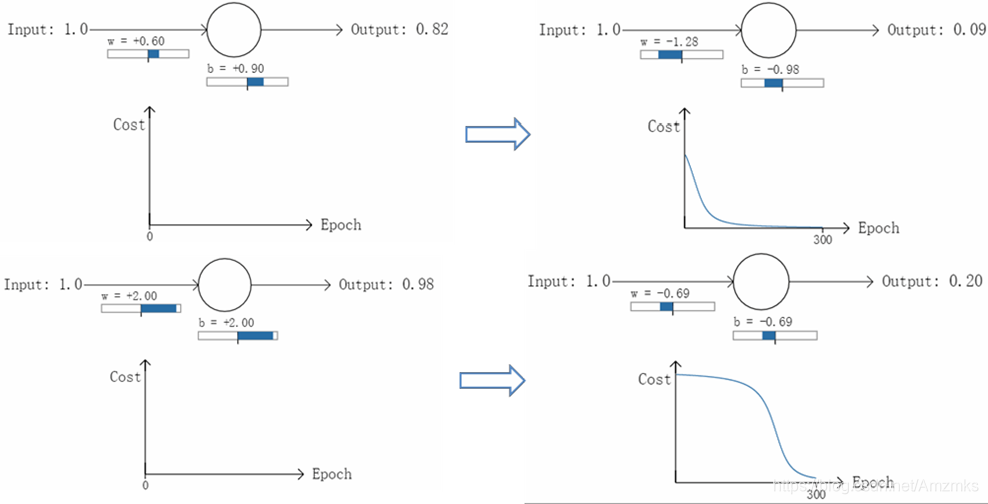
对于上面一个实验，sigmoid函数y=0.82对应的导数较大，而下面一个实验，y=0.98对应的导数较小：

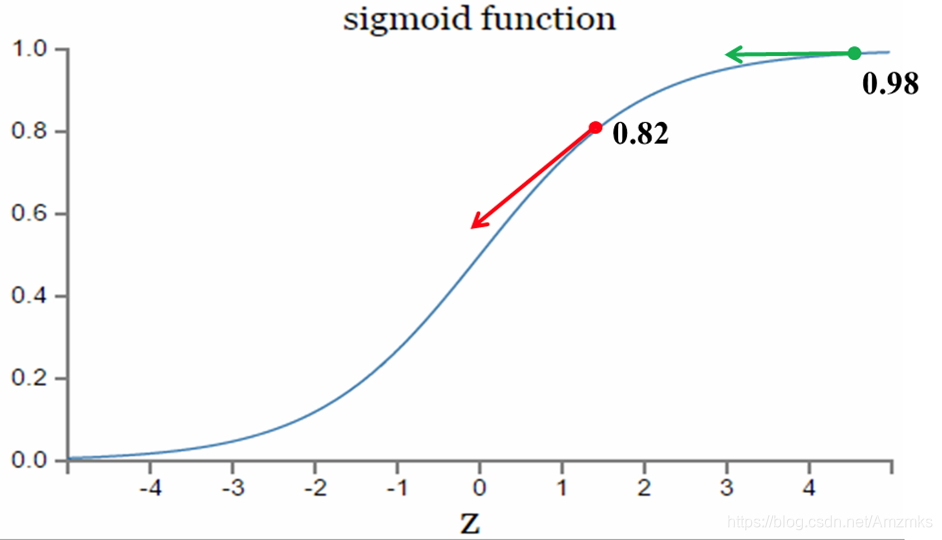
这样导致下面一个实验训练效果不好。

换一个思路，我们不改变激活函数，而是改变代价函数，用交叉熵代价函数：

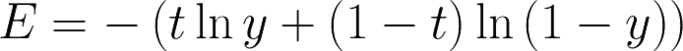
其中，t表示正确的标签，y表示网络的预测值。

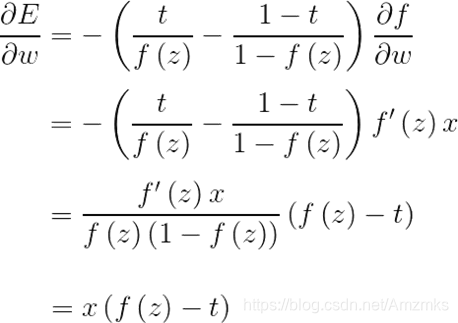
对于sigmoid激活函数：

当网络的真实值和预测值越接近，交叉熵E的值越小（接近于0）；反之，则接近无穷大。

例1：使用交叉熵代价函数实现MNIST案例。

from torch import nn, optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch

# 训练集
train_dataset = datasets.MNIST(root='./',
                               train=True,
                               transform=transforms.ToTensor(),
                               download=True)
# 测试集
test_dataset = datasets.MNIST(root='./',
                              train=False,
                              transform=transforms.ToTensor(),
                              download=True)

# 批次大小
batch_size = 64

# 装载训练集
train_loader = DataLoader(dataset=train_dataset,
                          batch_size=batch_size,
                          shuffle=True)

# 装载训练集
test_loader = DataLoader(dataset=test_dataset,
                         batch_size=batch_size,
                         shuffle=True)

for i, data in enumerate(train_loader):
    inputs, labels = data
    print(inputs.shape)
    print(labels.shape)
    break


# 定义网络结构
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(784, 10)
        self.softmax = nn.Softmax(dim=1)

    def forward(self, x):
        # ([64, 1, 28, 28])->(64,784)
        x = x.view(x.size()[0], -1)
        x = self.fc1(x)
        x = self.softmax(x)
        return x


LR = 0.5
# 定义模型
model = Net()
# 定义代价函数
# 修改1 代价函数使用交叉熵
mse_loss = nn.CrossEntropyLoss()
# 定义优化器
optimizer = optim.SGD(model.parameters(), LR)


def train():
    for i, data in enumerate(train_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 修改2 交叉熵本来就是（64,10）不需要one-hot
        # 交叉熵代价函数out(batch,C), labels(batch)
        loss = mse_loss(out, labels)
        # 梯度清0
        optimizer.zero_grad()
        # 计算梯度
        loss.backward()
        # 修改权值
        optimizer.step()


def test():
    correct = 0
    for i, data in enumerate(test_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 获得最大值，以及最大值所在的位置
        _, predicted = torch.max(out, 1)
        # 预测正确的数量
        correct += (predicted == labels).sum()
    print("Test acc:{0}".format(correct.item() / len(test_dataset)))


for epoch in range(10):
    print('epoch:', epoch)
    train()
    test()

输出：

torch.Size([64, 1, 28, 28])
torch.Size([64])
epoch: 0
Test acc:0.9051
epoch: 1
Test acc:0.9125
epoch: 2
Test acc:0.9172
epoch: 3
Test acc:0.919
epoch: 4
Test acc:0.9209
epoch: 5
Test acc:0.9216
epoch: 6
Test acc:0.924
epoch: 7
Test acc:0.9237
epoch: 8
Test acc:0.9244
epoch: 9
Test acc:0.9252

2. 对抗过拟合的方法

1）增大数据集

数据挖掘领域存在这样一句话，“有时候拥有更多的数据胜过一个好的模型”。一般来说更多的数据参与训练，训练得到的模型就越好。如果数据太少，而我们构建的神经网络又太复杂的话就比较容易产生过拟合的现象。

2）Early stopping

在训练模型的时候，我们往往会设置一个比较大的迭代次数。Early stopping便是一种提前结束训练的策略用来防止过拟合。一般的做法是记录到目前为止最好的validation accuracy，当连续10个epoch没有达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了。

3）正则化

L1正则化：

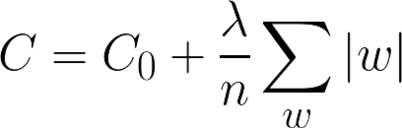
L2正则化：

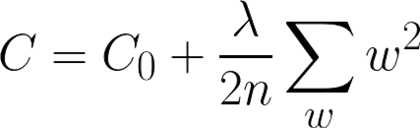
其中，C0代表原始的代价函数，n代表样本的个数，λ就是正则项系数，权衡正则项与C0项的比重。

L1正则化可以达到模型参数稀疏化的效果；L2正则化可以使得模型的权值衰减，使模型参数值都接近于0。

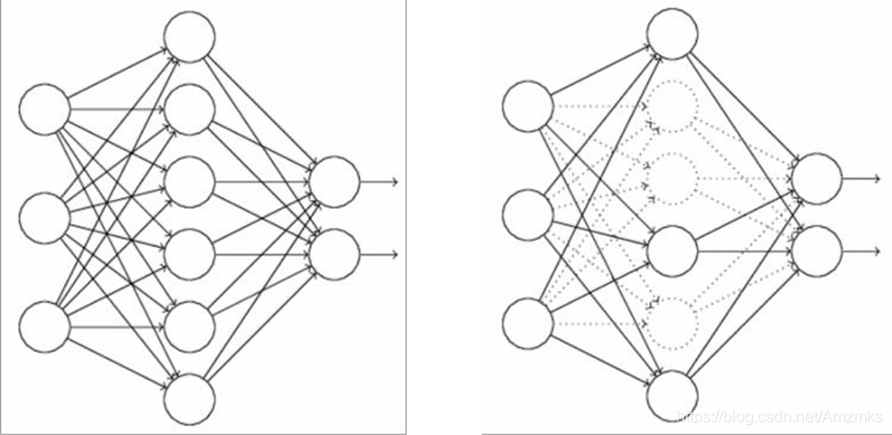
4）Dropout

左图是一个完整的神经网络结构。如右图，在训练时，每次训练随机选取一定比例的一些神经元不参与训练。在测试阶段时，所有神经元都工作。

例2：对MNIST案例使用Dropout。 

from torch import nn, optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch

# 训练集
train_dataset = datasets.MNIST(root='./',
                               train=True,
                               transform=transforms.ToTensor(),
                               download=True)
# 测试集
test_dataset = datasets.MNIST(root='./',
                              train=False,
                              transform=transforms.ToTensor(),
                              download=True)

# 批次大小
batch_size = 64

# 装载训练集
train_loader = DataLoader(dataset=train_dataset,
                          batch_size=batch_size,
                          shuffle=True)

# 装载训练集
test_loader = DataLoader(dataset=test_dataset,
                         batch_size=batch_size,
                         shuffle=True)

for i, data in enumerate(train_loader):
    inputs, labels = data
    print(inputs.shape)
    print(labels.shape)
    break


# 定义网络结构
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 修改1 定义多层网络结构
        self.layer1 = nn.Sequential(nn.Linear(784, 500), nn.Dropout(p=0.5), nn.Tanh())
        self.layer2 = nn.Sequential(nn.Linear(500, 300), nn.Dropout(p=0.5), nn.Tanh())
        self.layer3 = nn.Sequential(nn.Linear(300, 10), nn.Softmax(dim=1))

    def forward(self, x):
        # ([64, 1, 28, 28])->(64,784)
        x = x.view(x.size()[0], -1)
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x


LR = 0.5
# 定义模型
model = Net()
# 定义代价函数
mse_loss = nn.CrossEntropyLoss()
# 定义优化器
optimizer = optim.SGD(model.parameters(), LR)


def train():
    # 修改2 增加训练状态和测试状态
    # 训练状态
    model.train()
    for i, data in enumerate(train_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 交叉熵代价函数out(batch,C), labels(batch)
        loss = mse_loss(out, labels)
        # 梯度清0
        optimizer.zero_grad()
        # 计算梯度
        loss.backward()
        # 修改权值
        optimizer.step()


def test():
    # 测试状态
    model.eval()
    correct = 0
    for i, data in enumerate(test_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 获得最大值，以及最大值所在的位置
        _, predicted = torch.max(out, 1)
        # 预测正确的数量
        correct += (predicted == labels).sum()
    print("Test acc:{0}".format(correct.item() / len(test_dataset)))

    correct = 0
    for i, data in enumerate(train_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 获得最大值，以及最大值所在的位置
        _, predicted = torch.max(out, 1)
        # 预测正确的数量
        correct += (predicted == labels).sum()
    print("Train acc:{0}".format(correct.item() / len(train_dataset)))


for epoch in range(20):
    print('epoch:', epoch)
    train()
    test()

输出：

torch.Size([64, 1, 28, 28])
torch.Size([64])
epoch: 0
Test acc:0.9158
Train acc:0.91435
epoch: 1
Test acc:0.9307
Train acc:0.9320166666666667
epoch: 2
Test acc:0.941
Train acc:0.9416666666666667
epoch: 3
Test acc:0.944
Train acc:0.9472333333333334
epoch: 4
Test acc:0.9441
Train acc:0.9479
epoch: 5
Test acc:0.9481
Train acc:0.9518166666666666
epoch: 6
Test acc:0.9505
Train acc:0.9539833333333333
epoch: 7
Test acc:0.9552
Train acc:0.96085
epoch: 8
Test acc:0.9547
Train acc:0.9610166666666666
epoch: 9
Test acc:0.9593
Train acc:0.9651333333333333
epoch: 10
Test acc:0.96
Train acc:0.9656
epoch: 11
Test acc:0.9593
Train acc:0.9657
epoch: 12
Test acc:0.9628
Train acc:0.9690833333333333
epoch: 13
Test acc:0.962
Train acc:0.96905
epoch: 14
Test acc:0.9614
Train acc:0.9696833333333333
epoch: 15
Test acc:0.9626
Train acc:0.9714
epoch: 16
Test acc:0.9666
Train acc:0.97395
epoch: 17
Test acc:0.9656
Train acc:0.9736666666666667
epoch: 18
Test acc:0.9677
Train acc:0.9749333333333333
epoch: 19
Test acc:0.9634
Train acc:0.9722

例3：对MNIST案例使用正则化。

from torch import nn, optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch

# 训练集
train_dataset = datasets.MNIST(root='./',
                               train=True,
                               transform=transforms.ToTensor(),
                               download=True)
# 测试集
test_dataset = datasets.MNIST(root='./',
                              train=False,
                              transform=transforms.ToTensor(),
                              download=True)

# 批次大小
batch_size = 64

# 装载训练集
train_loader = DataLoader(dataset=train_dataset,
                          batch_size=batch_size,
                          shuffle=True)

# 装载训练集
test_loader = DataLoader(dataset=test_dataset,
                         batch_size=batch_size,
                         shuffle=True)

for i, data in enumerate(train_loader):
    inputs, labels = data
    print(inputs.shape)
    print(labels.shape)
    break


# 定义网络结构
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.layer1 = nn.Sequential(nn.Linear(784, 500), nn.Dropout(p=0.5), nn.Tanh())
        self.layer2 = nn.Sequential(nn.Linear(500, 300), nn.Dropout(p=0.5), nn.Tanh())
        self.layer3 = nn.Sequential(nn.Linear(300, 10), nn.Softmax(dim=1))

    def forward(self, x):
        # ([64, 1, 28, 28])->(64,784)
        x = x.view(x.size()[0], -1)
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x


LR = 0.5
# 定义模型
model = Net()
# 定义代价函数
mse_loss = nn.CrossEntropyLoss()
# 定义优化器
# 修改1 设置L2正则化
optimizer = optim.SGD(model.parameters(), LR, weight_decay=0.001)


def train():
    # 训练状态
    model.train()
    for i, data in enumerate(train_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 交叉熵代价函数out(batch,C), labels(batch)
        loss = mse_loss(out, labels)
        # 梯度清0
        optimizer.zero_grad()
        # 计算梯度
        loss.backward()
        # 修改权值
        optimizer.step()


def test():
    # 测试状态
    model.eval()
    correct = 0
    for i, data in enumerate(test_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 获得最大值，以及最大值所在的位置
        _, predicted = torch.max(out, 1)
        # 预测正确的数量
        correct += (predicted == labels).sum()
    print("Test acc:{0}".format(correct.item() / len(test_dataset)))

    correct = 0
    for i, data in enumerate(train_loader):
        # 获得一个批次的数据和标签
        inputs, labels = data
        # 获得模型预测结果（64,10）
        out = model(inputs)
        # 获得最大值，以及最大值所在的位置
        _, predicted = torch.max(out, 1)
        # 预测正确的数量
        correct += (predicted == labels).sum()
    print("Train acc:{0}".format(correct.item() / len(train_dataset)))


for epoch in range(20):
    print('epoch:', epoch)
    train()
    test()

输出：

torch.Size([64, 1, 28, 28])
torch.Size([64])
epoch: 0
Test acc:0.9054
Train acc:0.9047
epoch: 1
Test acc:0.9092
Train acc:0.90675
epoch: 2
Test acc:0.9217
Train acc:0.9200166666666667
epoch: 3
Test acc:0.9277
Train acc:0.9266333333333333
epoch: 4
Test acc:0.9229
Train acc:0.9228166666666666
epoch: 5
Test acc:0.9233
Train acc:0.9235166666666667
epoch: 6
Test acc:0.9341
Train acc:0.93375
epoch: 7
Test acc:0.9297
Train acc:0.9309166666666666
epoch: 8
Test acc:0.9351
Train acc:0.9361166666666667
epoch: 9
Test acc:0.9371
Train acc:0.93655
epoch: 10
Test acc:0.9297
Train acc:0.9316833333333333
epoch: 11
Test acc:0.9256
Train acc:0.9251
epoch: 12
Test acc:0.9313
Train acc:0.9309833333333334
epoch: 13
Test acc:0.9316
Train acc:0.9334333333333333
epoch: 14
Test acc:0.932
Train acc:0.93285
epoch: 15
Test acc:0.9323
Train acc:0.9362666666666667
epoch: 16
Test acc:0.9296
Train acc:0.9271666666666667
epoch: 17
Test acc:0.9306
Train acc:0.9311166666666667
epoch: 18
Test acc:0.9295
Train acc:0.9318
epoch: 19
Test acc:0.9332
Train acc:0.9335333333333333