matlab如何绘制传递函数对数幅频特性_Matlab仿真-控制系统频域分析

控制系统的时域分析虽然直观明了，但往往要求解复杂的微分方程，随着系统的复杂程度增加，微分方程的阶数也会增加，这样给系统的求解和分析带来了不便和巨大的工作量。

频域分析正是为了不求解微分方程就能够预示出系统的性能，而又能方便地指出应该如何调整系统以达到性能指标。

在引出什么是频域分析及其常用工具之前，我们先回顾下正弦信号及正弦量的一些基本知识。

1. 正弦量及其相量表示

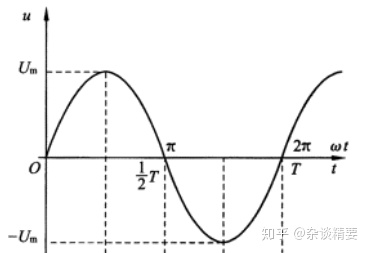
正弦电压和电流等物理量统称为正弦量。正弦量的特征表现在变化的快慢、大小及初始值三个方面，而它们分别由频率（或周期）、幅值（或有效值）和初相位来确定。

频率、幅值和初相位也被称为确定正弦量的三要素。

<1.1>频率与周期

正弦量变化一次所需的时间称为周期

（单位：秒）。每秒内变化的次数称为频率

（单位：Hz 赫兹）。

频率是周期的倒数：

正弦量变化的快慢除用周期和频率表示外，还可用角频率

表示。一周期内经历2π弧度，所以角频率

<1.2>幅值与有效值

正弦量在任一瞬间的值称为瞬时值，常用

分别表示电流、电压及电动势的瞬时值。瞬时值中最大的值称为幅值或最大值，常用

表示。

因此正弦电流的波形可用数学表达式表示为：

但我们通常都不用幅值来表示正弦电流、电压和电动势的大小，而是用有效值来表示，如平常我们所说的380V或220V电，都是指有效值。

有效值是从电流的热效应来规定的，某一个周期电流

通过电阻

在一个周期内产生的热量，和另一个直流电流

通过同样大小的电阻在相等的时间内产生的热量相等，那么这个周期性变化的电流

的有效值在数值上就等于这个直流电流

。

有效值与幅值的关系如下：

，

，

<1.3>初相位

正弦量

，其中

称为相位角或相位。

时的相位角称为初相位角或初相位。

<1.4>正弦量的相量表示

正弦量除了可以用上面提到的三角函数和正弦波形来表示，还可以用相量来表示。相量表示法的基础是复数，下面先回顾复数的表示方法，再说明如何用复数来表示正弦量。

设复平面中有一复数

，其模为

，幅角为

，那该复数可用以下三种方法表示：

代数式：

指数式：

极坐标式：

备注：由代数式推导出指数式，利用欧拉公式

，

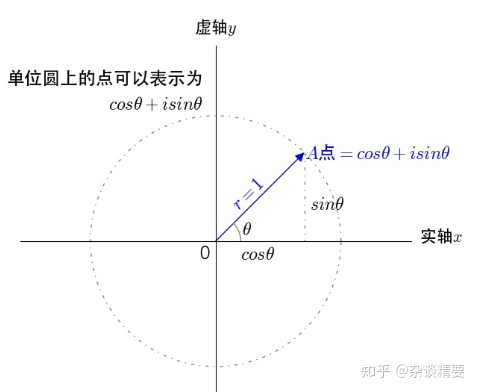
一个复数由模和幅角两个特征来确定，用复数来表示正弦量，则复数的模即为正弦量的幅值或有效值，复数的幅角即为正弦量的初相位。

例如正弦电流

可表示为

2.频率特性的定义

线性定常系统（或元件）的频率特性是零初始条件下稳态输出正弦信号与输入正弦信号的复数比，用

表示，则有

频率特性描述了在不同频率下系统（或元件）传递正弦信号的能力。

频率特性和传递函数之间还有个非常重要的关系，即传递函数的复变量

用

代替后，就相应地变为频率特性

3.频率特性的图形表示方法

用频率法分析、设计控制系统时，常常不是从频率特性的函数表达式出发，而是将频率特性绘制成一些曲线，借助这些曲线对系统进行图解分析。

下面介绍几种常用频率特性曲线及其图解，其中奈奎斯特（Nyquist）图和伯德（Bode）图使用较为广泛，会进行详细说明。

<3.1>频率特性曲线

频率特性曲线包括幅频特性曲线和相频特性曲线。幅频特性是频率特性幅值

随

的变化规律；相频特性是描述频率特性相角

随

的变化规律。

以RC电路举例：

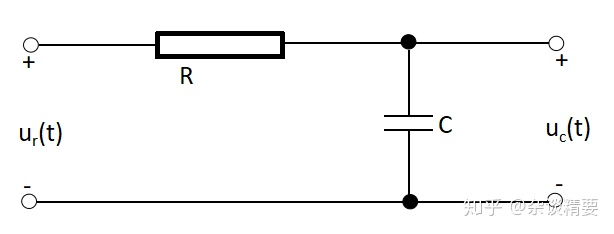
其传递函数：

绘制其频率特性曲线：

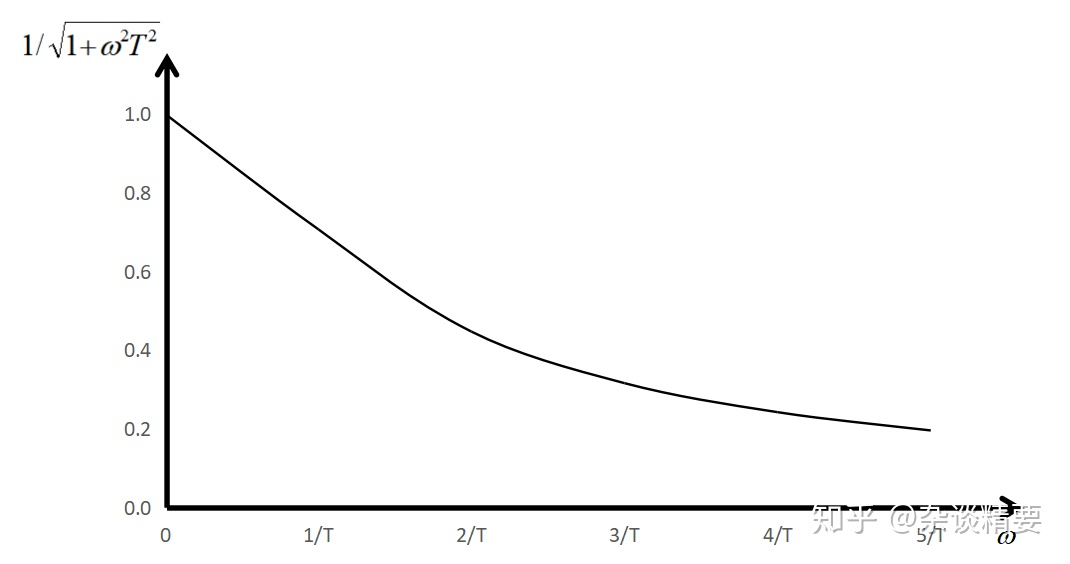
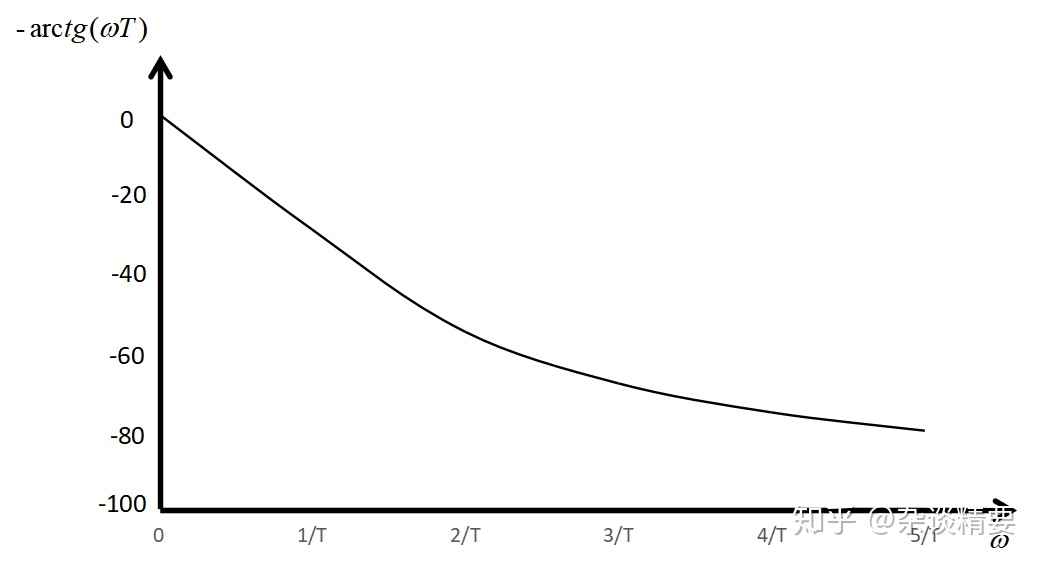
<3.2>幅相频率特性曲线

幅相频率特性曲线又称奈奎斯特（Nyquist）曲线，在复平面上以极坐标的形式表示。

绘制RC电路的幅相频率特性曲线：

clear,clc,close all;
g = tf(1,[1,1]);
nyquist(g);
grid;

备注：
tf函数是用来表示传递函数，tf(num,den)用来分别描述传递函数的分子分母系数
nyquist是绘制奈奎斯特曲线的函数

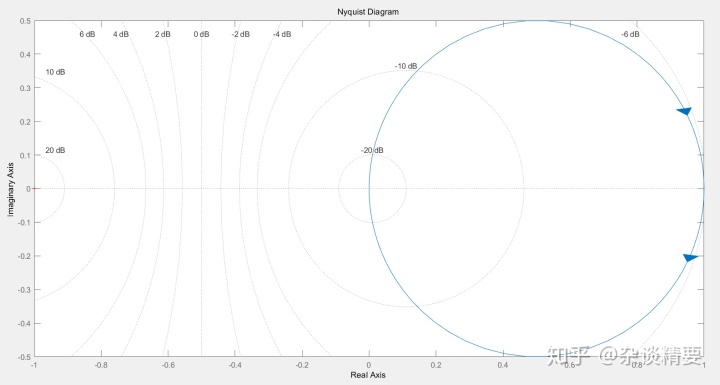
<3.3>对数频率特性曲线

对数频率特性曲线又称伯德（Bode）曲线。它由对数幅频特性和对数相频特性两条曲线组成，是频率法中应用最广泛的一组图线。伯德图是在半对数坐标纸上绘制出来的，横坐标采用对数刻度，纵坐标采用线性的均匀刻度。

伯德图中，对数幅频特性是

的对数值

和频率

的关系曲线；对数相频特性则是

的相角

和频率

的关系曲线。

绘制伯德图有个关键的概念——频程：

在横轴坐标上标明的数值是实际的

值，但坐标上的距离却是按

值的常用对数

来刻度的。坐标轴上任何两点

和

，

，则两点在横轴上距离为

。

频率

每变化10倍称为一个十倍频程，记作dec。每个dec在横坐标上的间隔为一个单位长度。

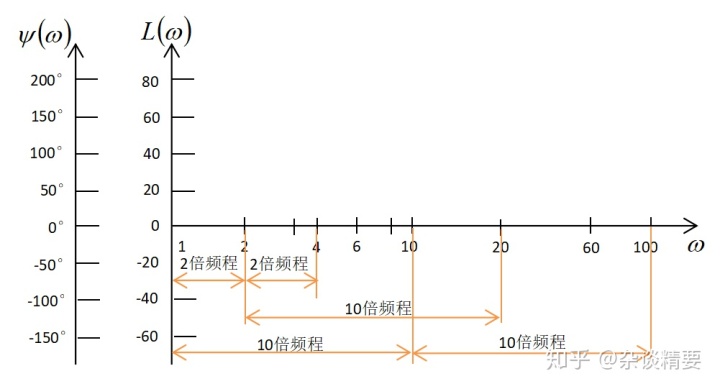
横坐标说完，伯德图的纵坐标都是线性分度，对数幅频特性纵轴数值

，即对数幅值乘上20倍，单位为分贝（dB）；对数相频特性纵轴数值即为

，单位为度（deg）。

绘制RC电路的对数频率特性曲线：

clear,clc,close all;
g = tf(1,[1,1]);
bode(g);
grid;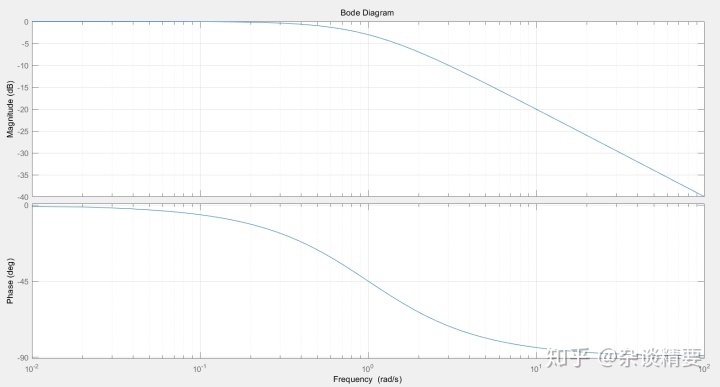

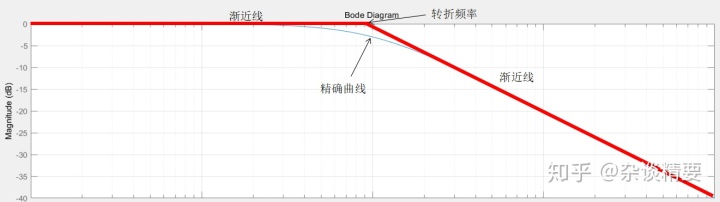
在控制系统初步设计时，可以利用渐近线来画伯德图，更简单方便：

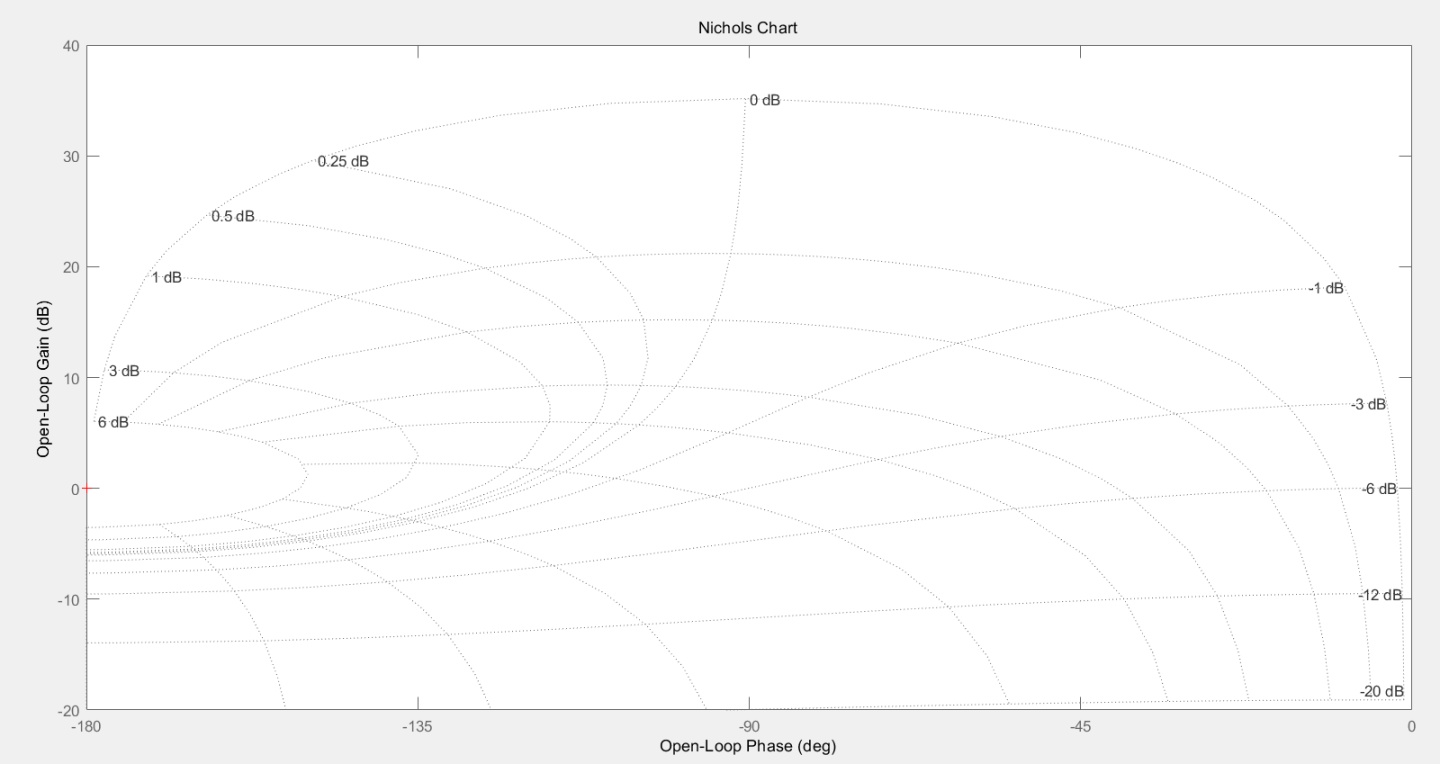
<3.4>对数幅相特性曲线

对数幅相特性曲线又称为尼克尔斯（Nichols）曲线。对数幅相特性是由对数幅频特性和对数相频特性合并而成的曲线。

对数幅相坐标的横坐标为相角

，纵轴为对数幅频值

，横纵坐标均是线性刻度。

绘制RC电路的对数幅相特性曲线：

clear,clc,close all;
g = tf(1,[1,1]);
nichols(g);
grid;
axis([-135,0,-40,0])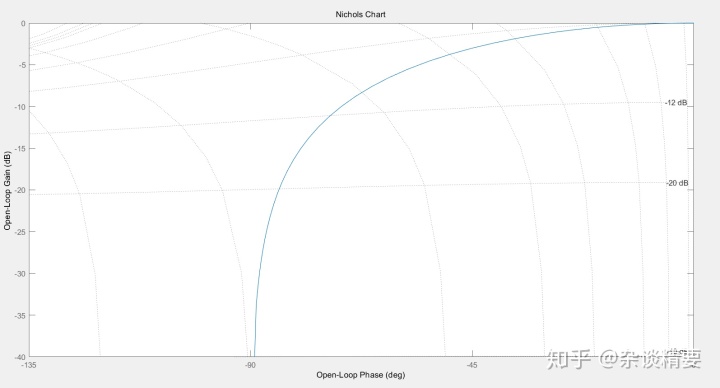

4.应用举例：利用Bode图分析汽车液压助力转向系统反馈

液压助力转向的原理如下图，为了便于分析，我们忽略车桥运动及转向管柱特性的影响，将其看作振动系统，简化其模型并列出运动方程：

其中m为齿条和液压油液的质量，b为系统的阻尼，k为系统的刚度，F(t)为随时间变化作用在齿条上的外力，x为齿条的位置。

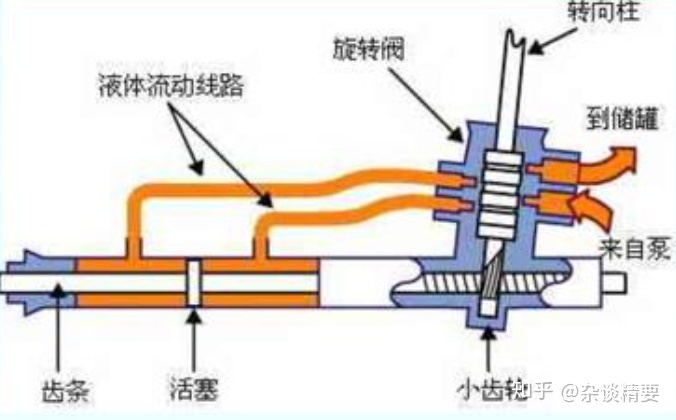
利用拉式变换可以得到系统的传递函数：

分别设置两组参数绘制系统Bode图，观察不同参数对系统性能的影响：

clear,clc,close all;
m1 = 1;
b1 = 1;
k1 = 1;
g1 = tf(1,[m1,b1,k1]);
bode(g1);
hold on;
m2 = 1;
b2 = 10;
k2 = 1;
g2 = tf(1,[m2,b2,k2]);
bode(g2);
grid;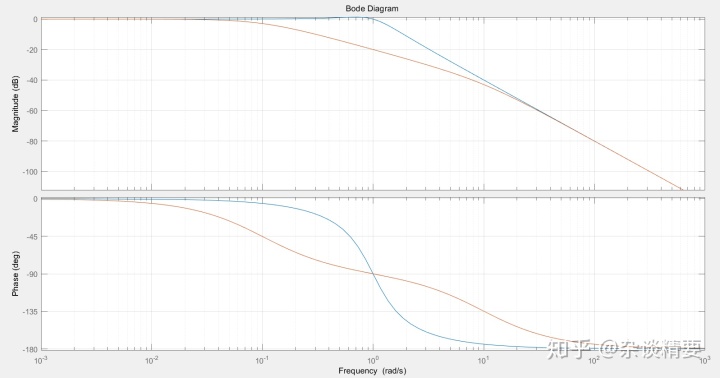

首先只看蓝色曲线，即

的g1曲线。随着频率的增大，响应的放大系数开始逐渐下降变小，相位角在逐渐增大，这种特性也就是常见的低通过滤器，频率越低越能反映输入的真实情况。

我们再一起看两条曲线，红色线g2是将阻尼系数提高了10倍（b2=10），可以看到系统幅值减小，转折频率向左移动变小，借助这样的分析可以帮助我们合理设计系统的参数。

关联文章阅读：

喜欢笔者的分享也可以搜索“杂谈精要”加下公众号支持一下。