稀疏矩阵
概念
- 对于一个矩阵,我们非常自然的是将其存储在一个二维数组a [ m ] [ n ] a[m][n]a[m][n]中,但对于一个矩阵,它的很多元素都为0,这样的矩阵我们叫做 “稀疏矩阵” ;
- 比如一个1000 × 1000 1000\times10001000×1000的矩阵,它只有1000 10001000个非零元素,如果我们用1000 × 1000 1000\times10001000×1000的数组存储的话,需要1000000 10000001000000个存储空间,同时在进行转置、乘法、加法时会花费大量时间,所以我们将进一步思考,如何更好的表示稀疏矩阵;
稀疏矩阵的表示
类似于”稀疏多项式“的表示方法(详细内容见:数据结构-数组-多项式),将矩阵中每个非零元素唯一表示为< r o w , c o l , v a l u e > <row,col,value><row,col,value>形式的三元组(假设v a l u e valuevalue为整数),非零元素按照由行到列的顺序排列,同时加上转置、乘法、加法等必要的操作,ADT定义如下:
//稀疏矩阵
class SparseMatrix;
//非零元素数据
class MatrixTerm
{
friend class SparseMatrix;
private:
int row, col, value;
};
class SparseMatrix
{
private:
//行数、列数、非零数
int rows, cols, terms;
//非零元素数组
MatrixTerm* smArray;
public:
//构造函数1
SparseMatrix(int r, int c, int t, int rs[],int cs[],int vs[]);
//构造函数2
SparseMatrix(int r, int c, int t);
//默认构造函数
SparseMatrix();
//转置矩阵
SparseMatrix Transpose();
//快速转置
SparseMatrix FastTranspose();
//扩展容量
void NewTerm(const int c, const int r, const int v);
//矩阵相加
SparseMatrix Add(SparseMatrix temp);
//矩阵相乘
SparseMatrix Multiply(SparseMatrix temp);
//重载=号,后续传参
const SparseMatrix& operator=(const SparseMatrix& temp);
//矩阵打印
void S_Show();
};
比如,对于下面的矩阵来说: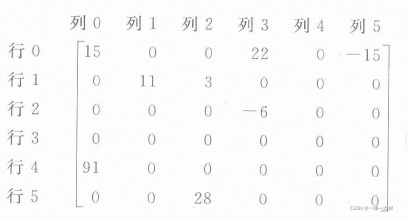
r o w s = 6 , c o l s = 6 , t e r m s = 8 , s m A r r a y 数 组 如 下 表 rows=6,cols=6,terms=8,smArray数组如下表rows=6,cols=6,terms=8,smArray数组如下表:
| r o w rowrow | c o l colcol | v a l u e valuevalue | |
|---|---|---|---|
| s m A r r a y [ 0 ] smArray[0]smArray[0] | 0 00 | 0 00 | 15 1515 |
| [ 1 ] [1][1] | 0 00 | 3 33 | 22 2222 |
| [ 2 ] [2][2] | 0 00 | 5 55 | − 15 -15−15 |
| [ 3 ] [3][3] | 1 11 | 1 11 | 11 1111 |
| [ 4 ] [4][4] | 1 11 | 2 22 | 3 33 |
| [ 5 ] [5][5] | 2 22 | 3 33 | − 6 -6−6 |
| [ 6 ] [6][6] | 4 44 | 0 00 | 91 9191 |
| [ 7 ] [7][7] | 5 55 | 2 22 | 28 2828 |
矩阵转置
一般方法
对于转置一个二维数组a [ r o w s ] [ c o l s ] a[rows][cols]a[rows][cols],我们一般用下面的方法:
for(int i=0; i<cols; i++)
for(int j=0; j<rows; j++)
b[i][j]=a[j][i];
那我门接下来将要用稀疏矩阵表示法实现矩阵转置:
实现函数
- 在思考前我们要注意smArray数组是 **按行有序**排列,所以虽然转置只是交换行号与列号,但排列顺序发生了变化,如下图:
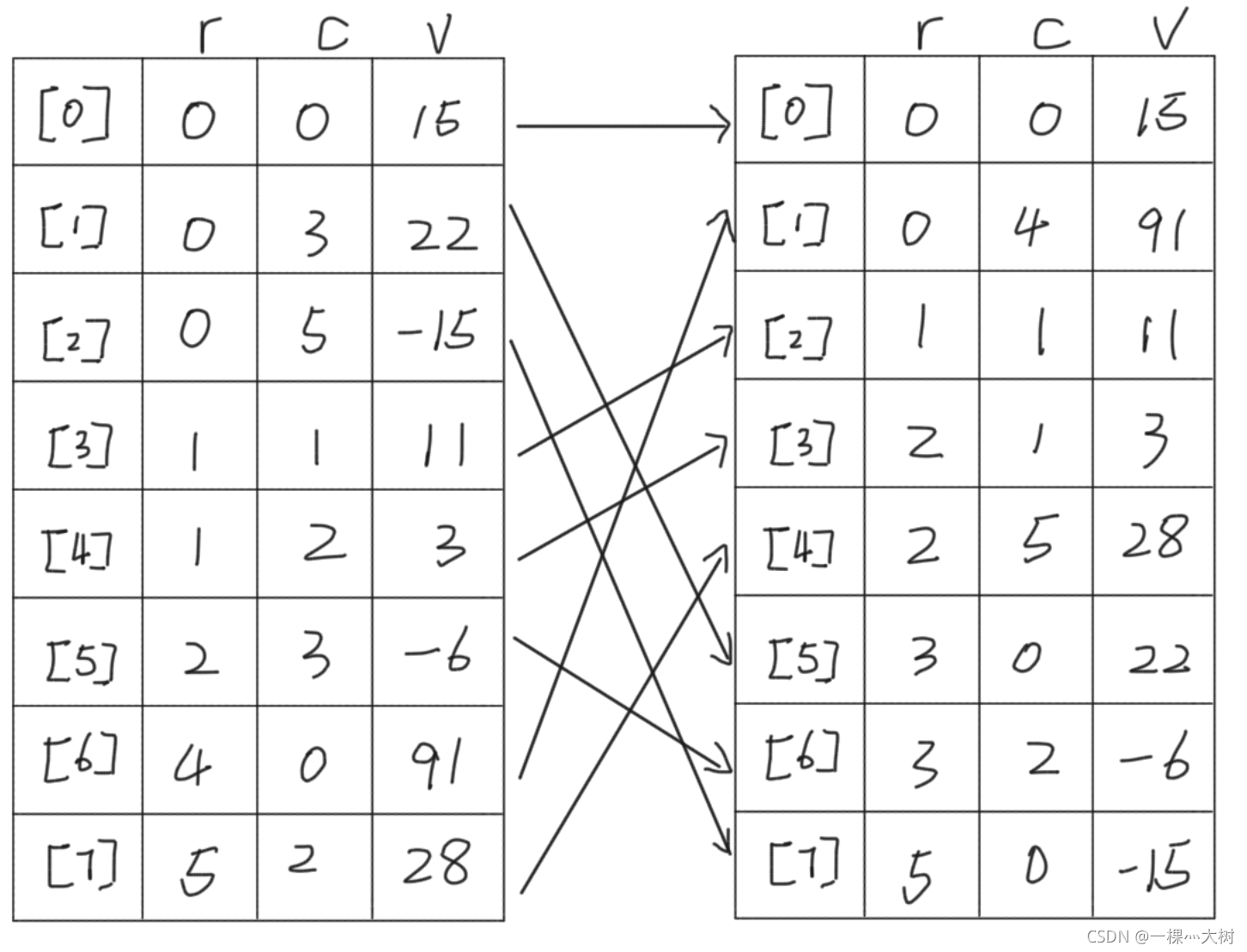
- 所以我们的目标就是将第i ii列的元素储存到第i ii行中,所以实现函数如下:
SparseMatrix SparseMatrix::Transpose()
{
cout << "转置矩阵:" << endl;
//含有非零元素
if (terms > 0)
{
SparseMatrix result(cols, rows, terms);
int bPos = 0;
for (int i = 0; i < cols; i++)
{
for (int j = 0; j < terms; j++)
{
//找到smArray中col等于i
if (smArray[j].col == i)
{
result.smArray[bPos].row = i;
result.smArray[bPos].col = smArray[j].row;
result.smArray[bPos++].value = smArray[j].value;
}
}
}
return result;
}
else return *this;
}
函数分析
- 从算法中看出,该函数的运行时间为O ( c o l s × t e r m s ) O(cols\times terms)O(cols×terms);
- 已知用二维数组表示是转置矩阵运行时间为O ( r o w s × c o l s ) O(rows\times cols)O(rows×cols),但用稀疏矩阵表示时,当t e r m s termsterms达到r o w s × c o l s rows\times colsrows×cols数量级时,此时转置的运行时间达到了O ( r o w s × c o l s 2 ) O(rows\times cols^2)O(rows×cols2),可见我们在节省内存空间时,可能浪费了大量的运行时间;
- 所以我们可以适当的使用些许内存获取r e s u l t . s m A r r a y result.smArrayresult.smArray的起始位置,将∗ t h i s *this∗this中元素逐个移到r e s u l t resultresult的正确位置上,接下来介绍这种实现方法,“快速转置”(FastTranspose)。
快速转置(FastTranspose)
实现函数
- 首先我们先定义两个数组:
- ∗ r o w S i z e *rowSize∗rowSize:r o w S i z e [ i ] rowSize[i]rowSize[i]表示 i ii列非零元素的数目 ;
- ∗ r o w S t a r t *rowStart∗rowStart:r o w S t a r t [ j ] rowStart[j]rowStart[j]表示t h i s − > s m A r r a y [ i ] this->smArray[i]this−>smArray[i]在r e s u l t . s m A r r a y [ j ] result.smArray[j]result.smArray[j]位置上,j = t h i s − > s m A r r a y [ i ] . c o l j=this->smArray[i].colj=this−>smArray[i].col
- *即rowStart[i]代表result中第i行(this中的第i)result.smArray[]的开始位置;
- 可以推出∗ r o w S t a r t *rowStart∗rowStart的计算公式为:
r o w S t a r t [ i ] = { 0 , i = 0 r o w S t a r t [ i − 1 ] + r o w S i z e [ i − 1 ] , 1 ≤ i ≤ c o l s rowStart[i]=\begin{cases} 0,i=0 \\ rowStart[i-1]+rowSize[i-1],1\le i\le cols \end{cases}rowStart[i]={0,i=0rowStart[i−1]+rowSize[i−1],1≤i≤cols
- 比如下面的矩阵:
r o w s = 6 , c o l s = 6 , t e r m s = 8 , s m A r r a y 数 组 如 下 表 rows=6,cols=6,terms=8,smArray数组如下表rows=6,cols=6,terms=8,smArray数组如下表:
| r o w rowrow | c o l colcol | v a l u e valuevalue | |
|---|---|---|---|
| s m A r r a y [ 0 ] smArray[0]smArray[0] | 0 00 | 0 00 | 15 1515 |
| [ 1 ] [1][1] | 0 00 | 3 33 | 22 2222 |
| [ 2 ] [2][2] | 0 00 | 5 55 | − 15 -15−15 |
| [ 3 ] [3][3] | 1 11 | 1 11 | 11 1111 |
| [ 4 ] [4][4] | 1 11 | 2 22 | 3 33 |
| [ 5 ] [5][5] | 2 22 | 3 33 | − 6 -6−6 |
| [ 6 ] [6][6] | 4 44 | 0 00 | 91 9191 |
| [ 7 ] [7][7] | 5 55 | 2 22 | 28 2828 |
两数组的取值如下表:
| 列数 | r o w S i z e rowSizerowSize | r o w S t a r t rowStartrowStart |
|---|---|---|
| [ 0 ] [0][0] | 2 22 | 0 00 |
| [ 1 ] [1][1] | 1 11 | 2 22 |
| [ 2 ] [2][2] | 2 22 | 3 33 |
| [ 3 ] [3][3] | 2 22 | 5 55 |
| [ 4 ] [4][4] | 0 00 | 7 77 |
| [ 5 ] [5][5] | 1 11 | 7 77 |
- 通过定义的两个数组确定函数定义,代码如下:
SparseMatrix SparseMatrix::FastTranspose()
{
cout << "进行快转置:" << endl;
if (terms > 0)
{
SparseMatrix result(cols, rows, terms);
int* rowSize = new int[cols];
int* rowStart = new int[cols];
fill(rowSize, rowSize + cols, 0);//rowSize全部填充为0
//统计*this每列(result每行)非0的数目
for (int i = 0; i < terms; i++)
rowSize[smArray[i].col]++;
//rowStart[i]代表result中第i行result.smArray[]的开始位置
rowStart[0] = 0;
for (int i = 1; i < cols; i++)
rowStart[i] = rowStart[i - 1] + rowSize[i - 1];
for (int i = 0; i < terms; i++)
{
int j = rowStart[smArray[i].col];
result.smArray[j].row = smArray[i].col;
result.smArray[j].col = smArray[i].row;
result.smArray[j].value = smArray[i].value;
rowStart[smArray[i].col]++;
}
//删掉缓存
delete[]rowSize;
delete[]rowStart;
return result;
}
else return *this;
}
函数分析:
- 通过分析算法可以得到整体算法的时间复杂度为O ( c o l s + t e r m s ) O(cols+ terms)O(cols+terms);
- 当t e r m s termsterms达到r o w s × c o l s rows\times colsrows×cols数量级时,O ( c o l s + t e r m s ) O(cols+ terms)O(cols+terms)变成了O ( c o l s × r o w s ) O(cols\times rows)O(cols×rows),与二维数组一样,但算法的常数因子大于二维数组算法;
- 当t e r m s termsterms比r o w s × c o l s rows\times colsrows×cols小的多时,算法既节省了空间和时间。
稀疏矩阵乘法
- 要实现矩阵a乘以矩阵b得到矩阵c前,要可以对矩阵实现smArray容量拓展,在不改变之前的数据,同时添加新的数据,代码如下:
void SparseMatrix::NewTerm(const int r, const int c, const int v)
{
MatrixTerm* temp = new MatrixTerm[terms + 1];
if (terms > 0)
{
//将旧smArray拷贝到temp中
copy(smArray, smArray + terms, temp);
//删除旧smArray
delete[]smArray;
}
//smArray指针指向temp
smArray = temp;
smArray[terms].row = r;
smArray[terms].col = c;
smArray[terms++].value = v;
}
函数实现
- 因为s m A r r a y smArraysmArray是按行排序,为了方便后矩阵的遍历 ,要将后矩阵进行转置,这样就可以在前矩阵的每一行遍历后矩阵的每一行(转置后),这样就可以实现矩阵乘法,具体代码如下:
SparseMatrix SparseMatrix::Multiply(SparseMatrix temp)
{
cout << "进行矩阵乘法:" << endl;
if (cols != temp.rows)throw"前矩阵列数不等于后矩阵行数,无法相乘!";
SparseMatrix result(rows, temp.cols, 0);
//将后矩阵进行转置,方便循环遍历
SparseMatrix temp_t = temp.FastTranspose();
//aPos:this->smArray索引;
//aPosNext:this->smArray下一行索引;
//rowIdex:result目前行数索引
int aPos = 0, aPosNext = 0;
int rowIdex = smArray[0].row;
int sum = 0;
while (aPos < terms)
{
//bPos:temp_t.smArray索引;
///colIdex:result目前列数索引
int bPos = 0;
int colIdex = temp_t.smArray[0].row;
while (bPos < temp_t.terms)
{
if (smArray[aPos].row != rowIdex)
{
result.NewTerm(rowIdex, colIdex, sum);
sum = 0;
aPos = aPosNext;
//矩阵temp下一列
while (temp_t.smArray[bPos].row == colIdex && bPos < temp_t.terms)
bPos++;
colIdex = temp_t.smArray[bPos].row;
}
else if (temp_t.smArray[bPos].row != colIdex)
{
result.NewTerm(rowIdex, colIdex, sum);
sum = 0;
aPos = aPosNext;
//矩阵temp下一列
colIdex = temp_t.smArray[bPos].row;
}
else
{
if (smArray[aPos].col < temp_t.smArray[bPos].col)
aPos++;
else if (smArray[aPos].col == temp_t.smArray[bPos].col)
{
sum += smArray[aPos].value * temp_t.smArray[bPos].value;
aPos++;
bPos++;
}
else
bPos++;
}
}
//矩阵this下一行
while (smArray[aPos].row == rowIdex && aPos < terms)
aPos++;
aPosNext = aPos;
rowIdex = smArray[aPos].row;
}
return result;
}
函数分析
- 通过分析算法,循环总耗时为O ( ∑ r ( b . c o l s × t r + b . t e r m s ) ) O(\sum_r(b.cols\times t_r+b.terms))O(∑r(b.cols×tr+b.terms)),其中t r t_rtr为第r rr行的非零元素数,极端情况下,循环的总耗时O ( ∑ r ( b . c o l s × t r + b . t e r m s ) ) = O ( b . c o l s × a . t e r m s + a . r o w s × b . t e r m s ) O(\sum_r(b.cols\times t_r+b.terms))=O(b.cols\times a.terms+a.rows\times b.terms)O(∑r(b.cols×tr+b.terms))=O(b.cols×a.terms+a.rows×b.terms);
- 与数组表示矩阵进行比较,算法为:
for(int i = 0; i<a.rows; i++)
for(int j=0; j<b.cols; j++)
{
sum=0;
for(int k = 0; k<a.cols; k++)
sum+=a[i][j] * b[k][j];
c[i][j] = sum;
{
- 该算法时间复杂度为O ( a . r o w s × a . c o l s × b . c o l s ) O(a.rows\times a.cols\times b.cols)O(a.rows×a.cols×b.cols),因为a . t e r m s ≤ a . r o w s × b . c o l s a.terms\le a.rows\times b.colsa.terms≤a.rows×b.cols,并且b . t e r m s ≤ a . c o l s × b . r o w s b.terms\le a.cols\times b.rowsb.terms≤a.cols×b.rows,所以还是稀疏矩阵表示时间开销更小。最坏情况下,算法较慢,但terms远小于最大值时,算法更加优越。
稀疏矩阵加法
- 加法并不是很复杂,循环遍历就好,代码如下:
SparseMatrix SparseMatrix::Add(SparseMatrix temp)
{
cout << "稀疏矩阵相加:" << endl;
if (rows != temp.rows || cols != temp.cols)throw"两矩阵行列数不相等,不能相加!!!";
int idxa = 0, idxb = 0;
SparseMatrix result(rows, cols, 0);
while (idxa < terms && idxb < temp.terms)
{
if (smArray[idxa].row < temp.smArray[idxb].row)
{
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value);
idxa++;
}
else if (smArray[idxa].row > temp.smArray[idxb].row)
{
result.NewTerm(temp.smArray[idxb].row, temp.smArray[idxb].col, temp.smArray[idxb].value);
idxb++;
}
else if (smArray[idxa].col < temp.smArray[idxb].col)
{
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value);
idxa++;
}
else if (smArray[idxa].col > temp.smArray[idxb].col)
{
result.NewTerm(temp.smArray[idxb].row, temp.smArray[idxb].col, temp.smArray[idxb].value);
idxb++;
}
else
{
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value + temp.smArray[idxb].value);
idxa++;
idxb++;
}
}
//未完全遍历
for (; idxa < terms; idxa++)
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value);
for (; idxb < temp.terms; idxb++)
result.NewTerm(temp.smArray[idxb].row, temp.smArray[idxb].col, temp.smArray[idxb].value);
return result;
}
多维数组
- 一种常用的表示方法:行主序法,即将多维数组展开为一维数组,这里不做详细介绍。
代码总览
- 可自己用数据测试;
#include <iostream>
using namespace std;
//稀疏矩阵
class SparseMatrix;
//非零元素数据
class MatrixTerm
{
friend class SparseMatrix;
private:
int row, col, value;
};
class SparseMatrix
{
private:
//行数、列数、非零数
int rows, cols, terms;
MatrixTerm* smArray;
public:
//构造函数1
SparseMatrix(int r, int c, int t, int rs[], int cs[], int vs[]);
//构造函数2
SparseMatrix(int r, int c, int t);
//默认构造函数
SparseMatrix();
//转置矩阵
SparseMatrix Transpose();
//快速转置
SparseMatrix FastTranspose();
//扩展容量
void NewTerm(const int c, const int r, const int v);
//矩阵相加
SparseMatrix Add(SparseMatrix temp);
//矩阵相乘
SparseMatrix Multiply(SparseMatrix temp);
//重载=号,后续传参
const SparseMatrix& operator=(const SparseMatrix& temp);
//矩阵打印
void S_Show();
};
SparseMatrix::SparseMatrix(int r, int c, int t, int rs[], int cs[], int vs[])
{
rows = r;
cols = c;
terms = t;
smArray = new MatrixTerm[terms];
for (int i = 0; i < terms; i++)
{
smArray[i].row = rs[i];
smArray[i].col = cs[i];
smArray[i].value = vs[i];
}
}
SparseMatrix::SparseMatrix(int r, int c, int t)
{
rows = r;
cols = c;
terms = t;
if (terms > 0)
smArray = new MatrixTerm[terms];
else smArray = NULL;
}
SparseMatrix::SparseMatrix()
{
rows = 0;
cols = 0;
terms = 0;
smArray = NULL;
}
SparseMatrix SparseMatrix::Transpose()
{
cout << "转置矩阵:" << endl;
if (terms > 0)
{
SparseMatrix result(cols, rows, terms);
int bPos = 0;
for (int i = 0; i < cols; i++)
{
for (int j = 0; j < terms; j++)
{
//找到smArray中col等于i
if (smArray[j].col == i)
{
result.smArray[bPos].row = i;
result.smArray[bPos].col = smArray[j].row;
result.smArray[bPos++].value = smArray[j].value;
}
}
}
return result;
}
else return *this;
}
SparseMatrix SparseMatrix::FastTranspose()
{
cout << "进行快转置:" << endl;
if (terms > 0)
{
SparseMatrix result(cols, rows, terms);
int* rowSize = new int[cols];
int* rowStart = new int[cols];
fill(rowSize, rowSize + cols, 0);//rowSize全部填充为0
//统计*this每列(result每行)非0的数目
for (int i = 0; i < terms; i++)
rowSize[smArray[i].col]++;
//rowStart[i]代表result中第i行result.smArray[]的开始位置
rowStart[0] = 0;
for (int i = 1; i < cols; i++)
rowStart[i] = rowStart[i - 1] + rowSize[i - 1];
for (int i = 0; i < terms; i++)
{
int j = rowStart[smArray[i].col];
result.smArray[j].row = smArray[i].col;
result.smArray[j].col = smArray[i].row;
result.smArray[j].value = smArray[i].value;
rowStart[smArray[i].col]++;
}
//删掉缓存
delete[]rowSize;
delete[]rowStart;
return result;
}
else return *this;
}
void SparseMatrix::NewTerm(const int r, const int c, const int v)
{
MatrixTerm* temp = new MatrixTerm[terms + 1];
if (terms > 0)
{
//将旧smArray拷贝到temp中
copy(smArray, smArray + terms, temp);
//删除旧smArray
delete[]smArray;
}
//smArray指针指向temp
smArray = temp;
smArray[terms].row = r;
smArray[terms].col = c;
smArray[terms++].value = v;
}
SparseMatrix SparseMatrix::Add(SparseMatrix temp)
{
cout << "稀疏矩阵相加:" << endl;
if (rows != temp.rows || cols != temp.cols)throw"两矩阵行列数不相等,不能相加!!!";
int idxa = 0, idxb = 0;
SparseMatrix result(rows, cols, 0);
while (idxa < terms && idxb < temp.terms)
{
if (smArray[idxa].row < temp.smArray[idxb].row)
{
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value);
idxa++;
}
else if (smArray[idxa].row > temp.smArray[idxb].row)
{
result.NewTerm(temp.smArray[idxb].row, temp.smArray[idxb].col, temp.smArray[idxb].value);
idxb++;
}
else if (smArray[idxa].col < temp.smArray[idxb].col)
{
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value);
idxa++;
}
else if (smArray[idxa].col > temp.smArray[idxb].col)
{
result.NewTerm(temp.smArray[idxb].row, temp.smArray[idxb].col, temp.smArray[idxb].value);
idxb++;
}
else
{
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value + temp.smArray[idxb].value);
idxa++;
idxb++;
}
}
//未完全遍历
for (; idxa < terms; idxa++)
result.NewTerm(smArray[idxa].row, smArray[idxa].col, smArray[idxa].value);
for (; idxb < temp.terms; idxb++)
result.NewTerm(temp.smArray[idxb].row, temp.smArray[idxb].col, temp.smArray[idxb].value);
return result;
}
SparseMatrix SparseMatrix::Multiply(SparseMatrix temp)
{
cout << "进行矩阵乘法:" << endl;
if (cols != temp.rows)throw"前矩阵列数不等于后矩阵行数,无法相乘!";
SparseMatrix result(rows, temp.cols, 0);
//将后矩阵进行转置,方便循环遍历
SparseMatrix temp_t = temp.FastTranspose();
//aPos:this->smArray索引;
//aPosNext:this->smArray下一行索引;
//rowIdex:result目前行数索引
int aPos = 0, aPosNext = 0;
int rowIdex = smArray[0].row;
int sum = 0;
while (aPos < terms)
{
//bPos:temp_t.smArray索引;
///colIdex:result目前列数索引
int bPos = 0;
int colIdex = temp_t.smArray[0].row;
while (bPos < temp_t.terms)
{
if (smArray[aPos].row != rowIdex)
{
result.NewTerm(rowIdex, colIdex, sum);
sum = 0;
aPos = aPosNext;
//矩阵temp一列
while (temp_t.smArray[bPos].row == colIdex && bPos < temp_t.terms)
bPos++;
colIdex = temp_t.smArray[bPos].row;
}
else if (temp_t.smArray[bPos].row != colIdex)
{
result.NewTerm(rowIdex, colIdex, sum);
sum = 0;
aPos = aPosNext;
//矩阵temp下一列
colIdex = temp_t.smArray[bPos].row;
}
else
{
if (smArray[aPos].col < temp_t.smArray[bPos].col)
aPos++;
else if (smArray[aPos].col == temp_t.smArray[bPos].col)
{
sum += smArray[aPos].value * temp_t.smArray[bPos].value;
aPos++;
bPos++;
}
else
bPos++;
}
}
//矩阵this下一行
while (smArray[aPos].row == rowIdex && aPos < terms)
aPos++;
aPosNext = aPos;
rowIdex = smArray[aPos].row;
}
return result;
}
const SparseMatrix& SparseMatrix::operator=(const SparseMatrix& temp)
{
cols = temp.cols;
rows = temp.rows;
terms = temp.terms;
if (smArray != NULL)
delete[]smArray;
if (terms > 0)
{
smArray = new MatrixTerm[terms];
copy(temp.smArray, temp.smArray + terms, smArray);
}
else smArray = NULL;
return *this;
}
void SparseMatrix::S_Show()
{
if (rows > 0 && cols > 0)
{
for (int i = 0; i < rows; i++)
{
cout << "[";
for (int j = 0; j < cols; j++)
{
int out = 0;
for (int t = 0; t < terms; t++)
{
if (smArray[t].row == i && smArray[t].col == j)
{
out = smArray[t].value;
}
}
cout << out << "\t";
}
cout << "]\n";
}
}
else cout << "[ ]\n";
cout << "稀疏矩阵信息:\n行数:" << rows << "\t列数:" << cols << "\t非零项数:" << terms << endl << endl;
}
int main()
{
int rs1[7] = { 0,0,1,1,3,5,7 }, rs2[10] = { 0,0,0,1,3,4,6,6,6,7 };
int cs1[7] = { 1,2,4,7,5,3,4 }, cs2[10] = { 0,3,8,4,2,5,2,4,7,6 };
int vs1[7] = { 20,11,23,45,13,6,16 }, vs2[10] = { 23,12,55,13,56,13,15,46,24,66 };
SparseMatrix a(8, 9, 7, rs1, cs1, vs1), b(8, 9, 10, rs2, cs2, vs2), c;
a.S_Show();
b.S_Show();
c = a.Transpose();
c.S_Show();
c = a.FastTranspose();
c.S_Show();
c = a.Multiply(c);
c.S_Show();
c = a.Add(b);
c.S_Show();
return 0;
}
上一篇:数据结构-数组-多项式
版权声明:本文为weixin_53580595原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。