区间覆盖问题
（1）题目描述
用i来表示x坐标轴上坐标为[i-1，i]的长度为1的区间，并给出M（1≤M≤200）个不同的整数，表示M个这样的区间。现在要求画几条线段覆盖住所有的区间，条件是：每条线段可以任意长，但是要求所画线段的长度之和最小，并且线段的数目不超过N(1≤N≤50）。
（2）解题思路
例如，给出M=5，整数1，3，4，8和11表示区间，要求所用线段不超过N=3条。
设置一个整型数组position[M]来表示所有的区间，假设position[M]已经按从小到大的顺序排好。
如果N≥M，那么用M条长度为1的线段可以覆盖住所有的区间，所求的线段总长为M。
如果N＜M，显然M＞1,可以按照如下的贪心策略来解决：
①如果N=1，即要用一条线段覆盖住所有区间，很显然所需线段总长即为position[M-1]-position[0]+1。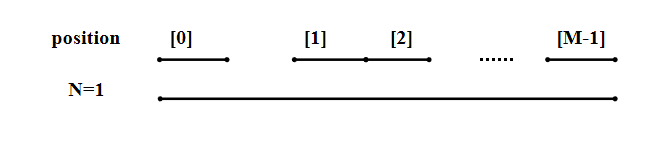
②如果N=2，即要用两条线段覆盖住所有区间，相当于把N=1中的线段分为两部分，各覆盖住左边与右边的区间。
如果线段在M个区间中不相邻的区间之间断开（如在position[0]与position[1]之间），左右两段线段的端点可调整到坐标position[0]+1与position[1]处，这样总长度小于断开之前。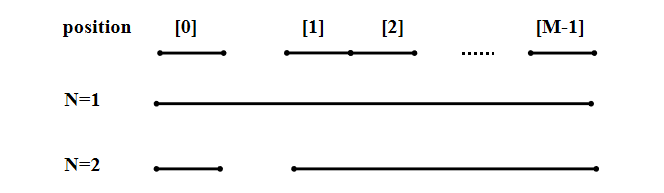
线段长度减少:position[1]-(position[0]+1)。
图中两条线段长度之和，比 原来一条线段长度减少了position[1]和position[0]+1之间的距离，即：
position[1]-position[0]-1。
题目要求最小线段总长，可以找间隔最大的两个相邻区间，在它们之间断开就可以了。这一过程相当于找
distance[i]=position[i]-position[i-1]-1
(1＜i＜M)的最大值。
如果N=3，相当于在N=2的方案下，将某条线段断成两截，并作可能的端点调整。
显然，为了得到当前情况下最小的总长度，同样应该在间隔最大的两个相邻区间之间断开。
如果原来的方案是N=2时总长最小的方案，这一操作可以得到N=3时总长最小的方案。
当N=k（k＞1）时依此类推，只需在N=k-1时最小总长的覆盖方案下，找到被同一条线段覆盖的间隔最大的两个相邻区间，“贪心”地从间隔处断开并适当调整两边线段的端点，就可以得到这是总长最小的方案。
#include <stdio.h>
#define N 200 // 区间数目的上限
void sort1(int value[],int n) // 排序函数（非递增）
{
int i,j,t;
for(i=0;i<n-1;i++)
for(j=0;j<n-1-i;j++)
if(value[j]<value[j+1])
{
t=value[j];
value[j]=value[j+1];
value[j+1]=t;
}
}
int main()
{
int m,i,n; // m是要覆盖的区间数，n是可用于覆盖的线段数
int position[N]; // 各个要覆盖的区间
int distance[N-1]; // 存放相邻区间的距离
printf("请输入要覆盖的区间数m= ");
scanf("%d",&m); // 输入要覆盖的区间数
printf("请输入 %d 个要覆盖的区间： ",m);
for(i=0;i<m;i++)
scanf("%d",&position[i]); // 输入m个区间
sort1(position,m); // m个区间降序排列
for(i=0;i<m-1;i++)
distance[i]=position[i]-position[i+1]-1;//计算相邻区间距离
sort1(distance,m-1); // m-1个区间距离降序排序
printf("请输入可使用的线段的总数n= ");
scanf("%d",&n); // 输入用于覆盖的线段数
if(n>=m)
{
printf("最小的线段总长为：%d\n",m);
return 0;
}
int nline=1; // 当前情况下所用线段总数
int totallength=position[0]-position[m-1]+1;
// 当前情况下所用线段总长
int devide=0; // 当前最大的未断开的区间距离
while((nline<n)&& // 还未达到可用线段总数
(distance[devide]>0)) // 还有不相邻的区间
{
nline++; // 再用一条线段
totallength -= distance[devide]; // 总长减少
devide++; // 覆盖该区间的线段断开，指向下一最大间隔
}
printf("最小线段总长为：%d\n",totallength);
return 0;
}