processing创意图形代码_Processing练习-Self Sketch - TAI CHI

又到了Processing练习。

这次是自画像练习，应老师要求利用processing或者P5.js绘制一幅自画像。

在课上老师给我们技术的同学们看了艺术专业同学们的自画像，有搞怪的，有精心设计的，还有令我最印象深刻的哪吒码绘（罗小黑大电影里边的那位）：

作者来自江南大学，具体信息不明，侵删。

不过，我的习惯是尽量不选择本能性想出的点子，所以描绘个人漫画式肖像的想法被我摒弃。

元素一——太极

最近半年时间内我都与中国传统道家文化打交道，无论是大创的游戏想要展现的中国哲学思想，还是Graphic Design课程作业中“太极无处不在”的思想，还是喜欢的小说中涉及的中国哲学思想，都让我感受到“道”文化的魅力。

虽然俺对于道家文化的了解不是很多，但是俺感觉已经被道家文化种草了。

道家文化中“太极”的概念尤为重要，所谓“是故，易有太极，是生两仪，两仪生四象，四象生八卦，八卦定吉凶，吉凶生大业。”

太极图案，在和谐统一中蕴含对称、正负型的美感

于是我想要把太极图案（PS：上学期的计算机图形课我也用OPENGL画了太极）融入到本次自画像中。

绘制太极的代码，在这里给出，其基本思路是画几个大小不同的圆或半圆，通过相互覆盖，最终形成太极图案：

注意，为了让太极有动态效果，我加入的变量有angle（旋转角度）、R（整个太极圆的直径），这样，在外部更改这些变量，最终呈现的太极就会发生变化。

  //taichi！注意，为了让太极有动态效果，我加入的变量有angle（旋转角度）、
  //R（整个太极圆的直径）
  float angleRad = radians(angle);
  //background(255, 10);
  fill(0, 255);
  noStroke();
  ellipse(width/2, height/2, R, R);
  fill(255, 255);
  arc(width/2, height/2, R, R, PI+angleRad, PI+PI+angleRad);
  float posX = cos(angleRad) * R/4 + width/2;
  float posY = sin(angleRad) * R/4 + height/2;
  float posX2 = cos(angleRad + PI) * R/4 + width/2;
  float posY2= sin(angleRad + PI) * R/4 + height/2;
  noStroke();
  ellipseMode(CENTER);
  ellipse(posX, posY, R/2, R/2);
  fill(0, 255);
  ellipse(posX, posY, R/6, R/6);
  ellipse(posX2, posY2, R/2, R/2);
  fill(255, 255);
  ellipse(posX2, posY2, R/6, R/6);

元素二——主角（没错就是我！）

其次，我想要把看小说时心目中侠客的形象描绘出来，那是一袭白衣或一身黑衫，头戴斗笠，深藏功与名。然后，由于processing适合绘制抽象图形，我便没有逆行其道去花时间描绘线条丰富、配色讲究的画像，而是偏向抽象、意向化的表达：

用简陋来描述再适合不过，但简单的线条和图形，却有点恰到好处的感觉

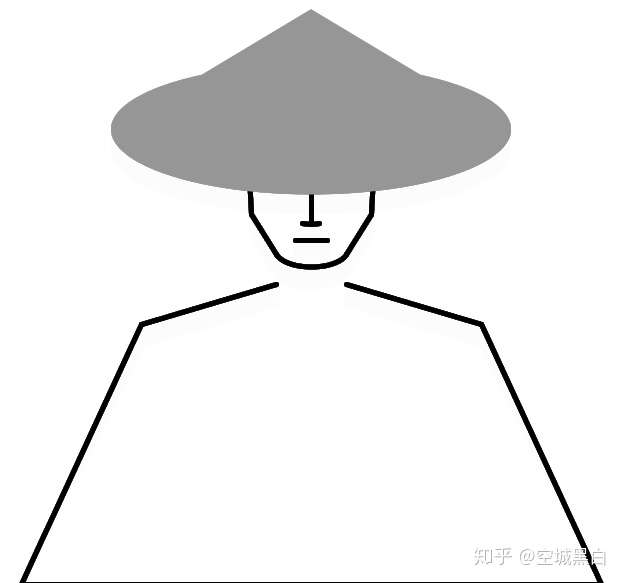
绘制过程挺枯燥的，不断调整绘制的参数、坐标等，使用到的函数包括：

Line / Curve / Arc / BeginShape / EndShape / Vertex / Ellipse，由于具体代码较为冗余，这部分代码在最后给出。整体人物的绘制，有一个参考点Y，有点类似锚点的概念，整体人物的绘制都是相对于这个参考点的。

还有小小的一点，就是为了模拟人物上下呼吸的运动，我使用了Sin函数，这样，整个人物就是上下缓慢运动的。这个时候刚才设置的参考点的作用就体现出来了。

有了太极和人物之后，还需要加入一些效果让整体内容富有层次感、画面感等，简单来说就是加点特效撑撑场面。

放飞自己的特效时间

一、飘雪

首先想到的就是在背景中加入飘动的雪花，提升整体的观感。

为秉持整体绘制风格的简单图形风格（才不是懒嘞！），雪花俺就用白色圆形来描绘，然后，加入拖尾的效果，整体感觉就出来了。

具体实现过程是写了一个Particle的类，生成200个雪花对象，分别管自己的移动、位置刷新和绘制。雪花粒子类的代码如下，这个类hin简单：

class CustomParticle{
  float posX;
  float posY;
  float velX;
  float velY;
  float r = 5.0f;
  
  public CustomParticle(float velX, float velY){
    this.posX = random(0,width);
    this.posY = random(0,height);
    this.velX = velX;
    this.velY = velY;
  }
  
  public void Move(){
    this.posX += velX;
    this.posY += velY;
  }
  
  public void CheckEdge(){
    if(posX > width) 
    {
      posX =0;
      posY = random(0,height);
    }
    if(posY > height) 
    {
      posY = 0;
      posX = random(0,width);
    }
  
  }
  
  public void Render()
  {
    ellipseMode(CENTER);
    ellipse(posX,posY,r,r);
  }
  
  public void Update(){
    Move();
    CheckEdge();
    Render();
  }

}

大雪花，慢速

小雪花，快速

二、远山

画完雪花，我想画一些能带给人实际前后景感觉的背景，可以是城池，可以是河岸，也可以是远山。

而且是会动的远山。

山形的绘制，关键函数在于Noise噪声函数，它适合用来描绘自然的曲线（数值）变化，用到山脉的形状描绘恰到好处。

void DrawMountain(float magnitute, float grayscale, float Y, float seed) {
  float x = 0;
  float y = seed;
  float thisMountY = Y;
  noStroke();
  fill(grayscale, 100);
  //draw the mountain using noise function.
  beginShape();
  vertex(0, height);
  while (x < width) 
  {
    vertex(x, thisMountY + magnitute * noise(x/100.0f, y));
    x = x + 1;
  }    
  vertex(width, height);
  endShape();
}

注意我加入的变量，magnitute控制山脉的起伏程度，grayscale顾名思义是绘制时的灰度，Y为山脉的基准线的y坐标，seed为noise函数的一个参数，它的变化会影响Noise函数的输出。Noise函数俺就不多讲了，大家可以去百度（GOOGLE）看看。

山体的移动就靠Y的变化来实现，同样，还是用sin函数来实现上下移动有快有慢的效果。（有没有朋友知道怎么描述这个运动特点，感觉我用的词好拙劣噢）

Processing：柏林噪声随机序列（Perlin Noise）也可以看看这个。