YOLOv3架构总结
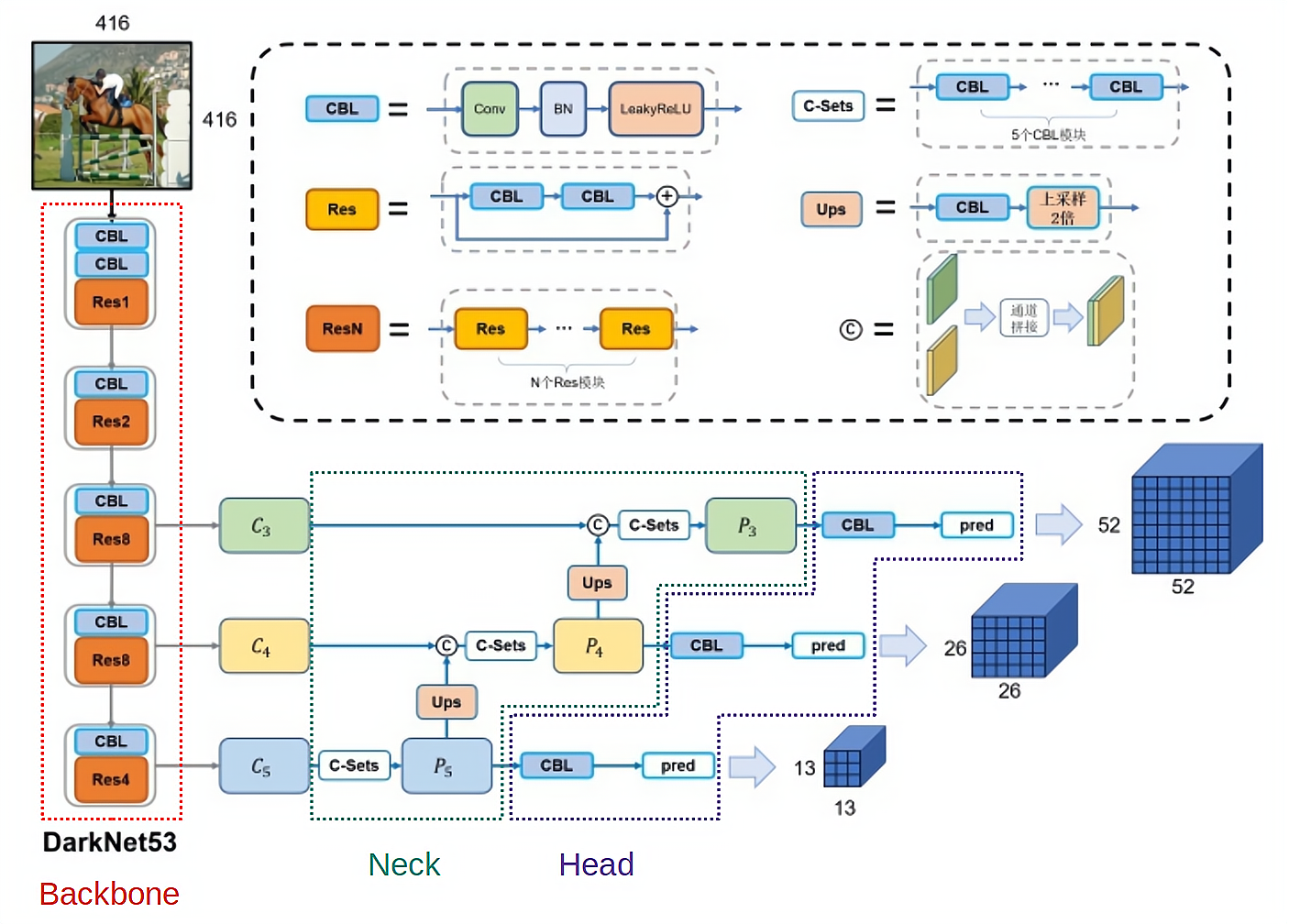
图来自: 搭建yolov3
前文总结:v3论文中(x,y,w, h) 为MSE,而官方代码中为下表。
| YOLO | Input | Backbone | Neck | Head | 置信度Loss | 坐标回归Loss | 分类Loss |
| v1 | 448*448 | GoogleNet | FC*2 | MSE | |||
| v2 | 32x | DarkNet-19 | Passthrough | Conv | MSE | ||
| v3 | 32x | DarkNet-53 | FPN | Conv | BCE | (x,y)BCE; (w,h)MSE | BCE |
模型细节
Backbone(DarkNet-53)

特点:
- 全卷积,无Maxpooling,靠stride=2的卷积下采样,依旧是通道加倍,宽高减半;
- 每个 Convolutional 和 DarkNet-19 一致(Conv + BN + LeakyReLU);
- 引进残差连接,提升网络的性能
Neck(FPN)

图来自:FPN

参考:FPN论文阅读
FPN论文中使用的是 Add,v3中是 concat
受图像金字塔启发,出现了 特征金字塔(FPN)。
YOLOv1和v2 大目标比小目标检测好,可能是因为降采样破坏了细节信息。因此,FPN论文中认为:CNN天然就是一个 金字塔,深层特征语义信息更多,浅层则细节信息更多。浅层网络负责检测较小的目标,深层网络负责检测较大的目标。考虑识别物体的类别依赖于语义信息,因此将深层网络的语义信息融合到浅层网络中去是个很自然的想法。
Head(多级检测)

YOLOv3使用多级检测。多级检测开始于SSD,如上图中C。思想:使用不同深度的特征图来检测不同大小的目标。而之前的YOLOv1和v2只使用最后一层特征图做检测。SSD则使用底层识别小目标,深层识别大目标。这是一种“分而治之”的思想。
显然,多级检测并不是来自于FPN,FPN只是一种特征融合的手段。正如SSD并没有特征融合,依旧是多级检测。我们可以使用其他特征融合方式,也可以使用多级检测。比如下图,虽然使用FPN,但是还是单级检测。

一般认为:只在顶层特征图上进行单级检测的检测器,小目标检测效果是不行的,但是未有定论。
其他细节
YOLOv3的先验框尺寸不同于YOLOv2,后者是除以了32,而前者是在原图尺寸上获得的,没有除以32。不懂,后续修改。
1. 图像预处理方式的调整
官方的YOLOv1和YOLOv2直接把图像调整成固定长度(如416×416或608×608)后,图像中的物体可能会发生畸变。如下图:

官方的YOLOv3采用下图办法。先把最长边调整到固定的尺度(如416或者608),而短边根据相应的比例调整即可。随后,再补充0即可,这样,物体畸变的问题就避免了。且一批图像都可以resize到相同的尺寸,方便我们后续将不同的图像组成batch去训练模型。

注意,新的resize方法显然会有效的像素会变少,因此,同样是416×416,两种方式得到的图像所包含的像素信息是显然有差距的,这一点会在性能上有直接的体现。不过,考虑到第一种方式会使得图像中的物体有显著的畸变,因此,综合来看,第二种方法还是更为合理、更加合适。
YOLOv3 损失函数
由于YOLOv3版本众多,每个版本的损失函数各有不同,以 原始pjreddie版本 讨论该问题。
理解YOLO 系列损失函数的关键在于理解正负样本。图像分类中每张图像是正样本,正样本的预测值和标签值求损失。而目标检测中,每张图像中的 Proposal区域 是样本,如何进行正负样本划分是理解损失函数的关键问题。
YOLOv3 中,输入416*416,通过s=2的Conv进行降采样,加FPN特征融合,得到 13 *13,26*26,52*52的特征图。每个 grid cell 对应原图中的一块区域,也就是一块感受野。这种卷积架构的设计使得我们称“图像被分成了多少个小格”。
假设我们只考虑一种尺度,那么损失函数如何计算,从而更新权重拟合数据?
先考虑什么是负样本?
YOLOv3 遍历每个cell,每个cell 有3个 Anchor,对应着就有3个预测框。对于每个预测框和所有的图像中的标注框计算IOU,取最大的IOU为maxIOU,如果maxIOU < 0.5,那么为负样本。只计算置信度损失。
负样本置信度损失
不同于v2中使用 MSELoss,v3中使用BCELoss。负样本的标签为 0.
那么什么是正样本?
和v2一样。遍历每个标注框,获得 标注框中心点对应的那个cell 索引。该cell 中有 有3个 Anchor,对应着就有3个预测框。计算该 标注框和每个 Anchor 的最大IOU【(x,y)移动到(0,0),只考虑形状】,记为 。那么该Anchor 对应的图像区域即正样本。
正样本
置信度损失
正样本的置信度损失和负样本一样采用 BCELoss。正样本的标签为 1.
坐标损失
xy:BCE
wh:MSE
分类损失
分类损失采用BCE,主要是因为 Open-set 问题。
总损失
注:以上损失,带 hat 的表示标签,不带的为 预测值。
思考
1. v2 和 v3 损失函数有什么区别?
相同点:
- 正负样本划分方法相同
- (w,h)损失都是MSE
不同点:
- 每个cell 的anchor 数目不同,v2 为5个,v3 为 3个。
- v2置信度损失为:MSE;v3为BCE。
- (x,y)损失:v2是MSE;v3 是BCE
- 分类损失:v2是MSE;v3 是BCE
2. 为什么 (x,y) 损失可以使用 BCE?
,令导数=0,可得 x =
取得最小值:
所以,BCELoss 不仅仅是可以用在 二分类 损失中,(x,y)的回归依然可以使用。

上面的(x, y)的损失并不精确,下面写一个具体的:
;
代码中直接 weights+lr*delta,所以是实际算的时候梯度是上面等式的相反数,所以:
下面的tx 即 。
float delta_yolo_box(box truth, float *x, float *biases, int n, int index, int i, int j, int lw, int lh, int w, int h, float *delta, float scale, int stride)
{
box pred = get_yolo_box(x, biases, n, index, i, j, lw, lh, w, h, stride);
float iou = box_iou(pred, truth);
float tx = (truth.x*lw - i);
float ty = (truth.y*lh - j);
float tw = log(truth.w*w / biases[2*n]);
float th = log(truth.h*h / biases[2*n + 1]);
delta[index + 0*stride] = scale * (tx - x[index + 0*stride]);
delta[index + 1*stride] = scale * (ty - x[index + 1*stride]);
delta[index + 2*stride] = scale * (tw - x[index + 2*stride]);
delta[index + 3*stride] = scale * (th - x[index + 3*stride]);
return iou;
}对于输出的x,forward时候已经做了 sigmoid变换(logistic激活函数)
void forward_yolo_layer_gpu(const layer l, network net)
{
copy_gpu(l.batch*l.inputs, net.input_gpu, 1, l.output_gpu, 1);
int b, n;
for (b = 0; b < l.batch; ++b){
for(n = 0; n < l.n; ++n){
int index = entry_index(l, b, n*l.w*l.h, 0);
activate_array_gpu(l.output_gpu + index, 2*l.w*l.h, LOGISTIC);
index = entry_index(l, b, n*l.w*l.h, 4);
activate_array_gpu(l.output_gpu + index, (1+l.classes)*l.w*l.h, LOGISTIC);
}
}
if(!net.train || l.onlyforward){
cuda_pull_array(l.output_gpu, l.output, l.batch*l.outputs);
return;
}
cuda_pull_array(l.output_gpu, net.input, l.batch*l.inputs);
forward_yolo_layer(l, net);
cuda_push_array(l.delta_gpu, l.delta, l.batch*l.outputs);
}
所以:
delta = scale * (tx - x);
对于y,以上同理。
3. L(x,y) 和L(w,h) 中  怎么算出来的?
怎么算出来的?
是标记框的坐标。
步骤一:将原始标记框按原始图像到416×416尺寸变换比例同比例缩放到符合416×416尺寸的大小(简单说就是因为网络输入是416×416大小,所以输入图像会先reshape到这个尺寸,这时要将标记框也同比例进行缩放),然后计算标记框中心点坐标和宽高值。
步骤二:计算标记框在feature map上的中心点坐标和宽高值。将上一步得到的标记框中心点坐标和宽高值都除以stride(比如feature map为13×13,此时stride=416/13=32),得到标记框在feature map上位置信息:
步骤三:计算标记框相对于anchor box的偏移量和尺度缩放大小。使用下面公式:
其中, 为feature map上grid cell左上角坐标,
为anchor box在feature map上宽高大小,通过将标记框宽高与anchor box宽高比值的对数计算它们的缩放比例,通过取对数而不是直接预测相对形变
,是因为如果直接计算相对形变,那么要求预测w值要大于0,因为框的宽高不可能为负数,因此,该问题变成一个有不等式条件约束的优化问题,没法直接用SGD来做,所以先取一个对数变换将这个不等式约束去掉就可以了。
至此,我们对标记框的偏移量和尺度缩放大小就求出来了,损失函数里面就可以使用作为标记框数据参与运算了。
4. 损失函数中(x, y, w, h)是什么?
网络输出为 的范围可以是任何值,使用 sigmoid 函数将其约束到(0,1)内,因此(x, y, w, h)为:

5. 损失函数中置信度C和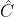 是什么?
是什么?
标注框的:负样本则为0,正样本为1。对于
标记框相应类别概率设为1,其他设置为0。
6. 置信度中的 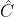 是否可以为 IOU(预测框,标注框)?
是否可以为 IOU(预测框,标注框)?
当然可以。不过,v3 官方实现中,正样本的直接设置为1,负样本的设置为 0,直接当成2分类, 可能更简单吧。
根据上面的 BCE 的求导可知,BCE 可以作为回归损失。
参考:3.4 YOLO入门教程:YOLOv3(4)-损失函数 - 知乎
正负样本理解
和YOLOv2 一样。上面内容已经描述。
推理
1. 网络输出为 ,那如何还原到原图上?
- 步骤1:其中W,H分别代表feature map的尺寸大小,比如最后输出feature map为13×13,则W=13,H=13。这样我们得到了正对于输入图片416×416的归一化预测框。
- 步骤2:最终预测框
- 但是我们原图往往不是416×416大小,是经过了reshape到416尺寸的操作,所以我们还需要将得到的归一化预测框reshape回去到符合原图尺寸比例的归一化预测框:直接乘以原图尺寸大小就可以得到最终的预测框。
2. 后处理同YOLOv2。
YOLOv3的优缺点
优点:
- 相对v2,小目标检测效果提升
- 全卷积Backbone
- FPN多尺度特征融合的Neck
- 多级检测
缺点:
- 相对v2,中等和大尺寸目标上相对弱一些
如何优化YOLOv3?
- 优化Backbone
- 优化Neck:如加入SPP
- 优化正负样本匹配策略
- 改进loss 函数
- ......
参考
https://github.com/pjreddie/darknet/blob/master/src/yolo_layer.c
(最简单)深度理解YOLOV3损失函数及anchor box_恩泽君的博客-CSDN博客_yolov3损失函数
代码注释:https://github.com/BBuf/Darknet/blob/master/src/yolo_layer.c