vector扩容原理
- Vector通过一个连续的数组存放元素,如果集合已满,在新增数据的时候,就要分配一块更大的内存,将原来的数据复制过来,释放之前的内存,在插入新增的元素;
- 对vector的任何操作,一旦引起空间重新配置,指向原vector的所有迭代器就都失效了 ;
- 不同的编译器实现的扩容方式不一样,VS2019中以1.5倍扩容,GCC以2倍扩容。
vector扩容代码示例:
#include<iostream>
#include<vector>
using namespace std;
int main()
{
vector<int> cap;
cout << cap.capacity() << endl;
for (int i = 0; i < 10; i++)
{
cap.push_back(i);
cout << "size: " << cap.size() << endl;
cout << "capacity: " << cap.capacity() << endl;
}
return 0;
}
VS2019执行代码结果:1.5倍扩容机制
GCC执行代码结果:2倍扩容机制
根据上述代码在不同编译器中的执行结果得出两个问题:
- 为什么要成倍的扩容而不是一次增加一个固定大小的容量呢?
- 为什么是以2倍或1.5倍的方式扩容而不是其他倍数呢?
第一个问题:以成倍方式增长
3. 假定有 n 个元素,倍增因子为 m
4. 完成这 n 个元素往一个 vector 中的 push_back操作,需要重新分配内存的次数大约为 logm(n)
5. 第 i 次重新分配将会导致复制 m^(i) (也就是当前的vector.size() 大小)个旧空间中元素
6. n 次 push_back 操作所花费的时间复制度为O(n)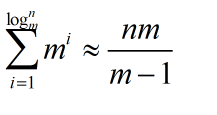
7. m / (m - 1)是一个常量,均摊分析的方法可知,vector 中 push_back 操作的时间复杂度为常量时间
一次增加固定值大小
- 假定有 n 个元素,每次增加k个
- 第i次增加复制的数量为为:100i
- n 次 push_back 操作所花费的时间复杂度为O(n^2)
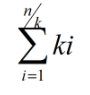
- 均摊下来每次push_back 操作的时间复杂度为O(n)
问题一小结
对比可以发现采用采用成倍方式扩容,可以保证常数的时间复杂度,而增加指定大小的容量只能达到O(n)的时间复杂度,因此使用成倍的方式扩容。
第二个问题:为什么是以2倍或1.5倍的方式扩容而不是其他倍数呢?
- 根据查阅的资料显示,考虑可能产生的堆空间浪费,成倍增长倍数不能太大,使用较为广泛的扩容方式有两种,以2二倍的方式扩容,或者以1.5倍的方式扩容。
- 以2倍的方式扩容,导致下一次申请的内存必然大于之前分配内存的总和,导致之前分配的内存不能再被使用,所以最好倍增长因子设置为(1,2)之间:
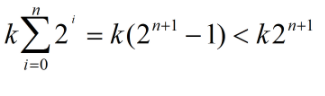
用一张图来说明2倍扩容与1.5倍扩容的区别:
问题二小结
使用2倍(k=2)扩容机制扩容时,每次扩容后的新内存大小必定大于前面的总和。
而使用1.5倍(k=1.5)扩容时,在几次扩展以后,可以重用之前的内存空间了。
总结
- vector在push_back以成倍增长可以在均摊后达到O(1)的事件复杂度,相对于增长指定大小的O(n)时间复杂度更好。
- 为了防止申请内存的浪费,现在使用较多的有2倍与1.5倍的增长方式,而1.5倍的增长方式可以更好的实现对内存的重复利用。
版权声明:本文为qq_37535749原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。