1 表达式

$F(n)=\{\begin{array}{ll}1& n=0,1\\ F(n-1)+F(n-2)& n>1\end{array}$

2 代码

public static int fib(int n){
	if (n == 0 || n == 1) return 1;
	else{
		return fib(n-1) + fib(n-2);
	}
}

3 复杂度分析

3.1 空间复杂度

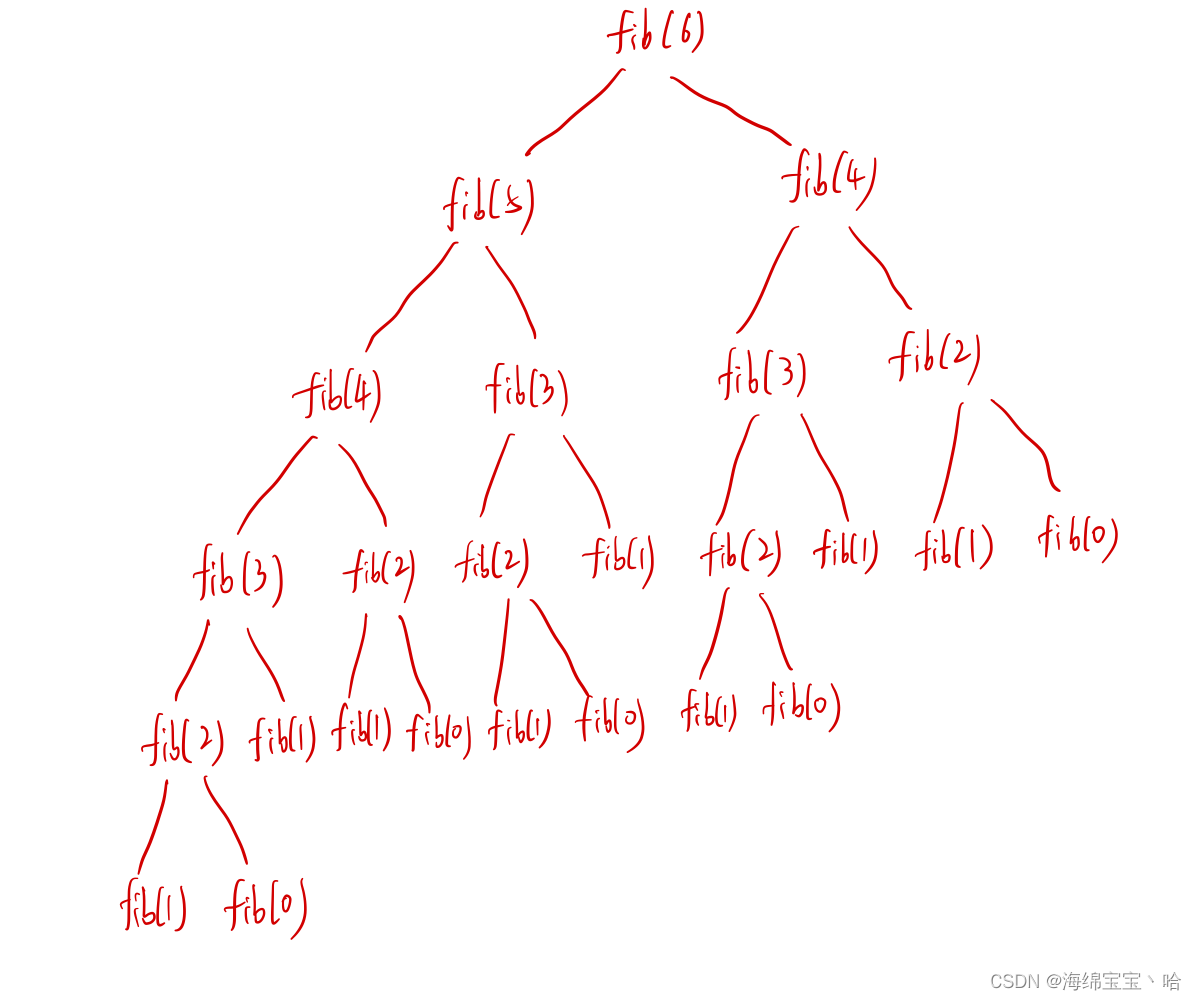
• 每次调用函数都要一个空间来存储传进来的整数，并且函数运行完成并返回时，空间被释放，因此空间复杂度为树的深度$n$，即$O(n)$

3.2 时间复杂度

• 上图中时间复杂度相当于所有节点的个数，不是完全二叉树，但是还是指数级别的，因此时间复杂度为$O(2^n)$

3.3 问题

• 非递归时间复杂度和空间复杂度为多少？

• 代码：

  public static int fib(int n){
  	int front=1;
  	int behind=1;
  	int temp;
  	for(int i = 2;i <= n-1;i++){
  		temp = front + behind;
  		front = behind;
  		behind = temp;
  	}
  	return behind;
  }
  

  • 空间复杂度：由于程序运行中只用了有限个变量，且与问题规模n无关，所以空间复杂度为$O(1)$
  • 时间复杂度：一层for循环，一共执行了n-2次，所以时间复杂度为$O(n)$