目录
一 、首先了解堆是什么
1、概念:堆是一种数据结构,一种叫做完全二叉树的数据结构。
2、性质:
大根堆:每个结点的值都大于其左孩子和右孩子结点的值,称之为大根堆;
代码表示:arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]
小根堆:每个结点的值都小于其左孩子和右孩子结点的值,称之为小根堆。
代码表示:arr[i] <= arr[2i + 1] && arr[i] <= arr[2i + 2]
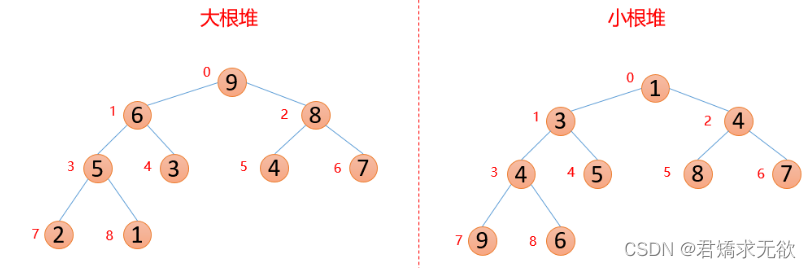
大根堆映射在数组中为{9,6,8,5,3,4,7,2,1};
小根堆映射在数组中为{1,3,4,4,5,8,7,9,6};
对于这些元素本质上我们还是放在数组中,只是我们把它看成堆的形式,方便我们操作。
重点:索引一个元素的父结点跟该元素的左孩子和右孩子:
父结点索引:(i-1)/2;//i为对应数组元素下标
左孩子索引:2*i+1;
右孩子索引:2*i+2;
二、排序基本步骤
堆排序的基本思想是:
1、将带排序的序列构造成一个大顶堆,根据大顶堆的性质,当前堆的根节点(堆顶)就是序列中最大的元素;
2、将堆顶元素和最后一个元素交换,然后将剩下的节点重新构造成一个大顶堆;
3、重复步骤2,如此反复,从第一次构建大顶堆开始,每一次构建,我们都能获得一个序列的最大值,然后把它放到大顶堆的尾部。最后,就得到一个有序的序列了。
2.1、构造堆
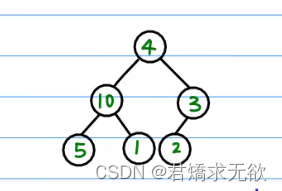
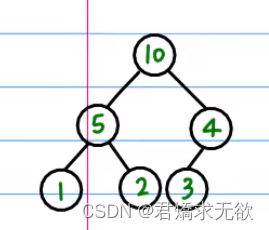
1、假如有这样一组数据,我们要把它变成一个大根堆,显然在10这棵树中是满足堆条件10 > 5 && 10 > 1 , 同时在3这棵树中也是满足的,现在只有4这棵树不满足,我们发现在{4, 10, 3}这三个数中10 最大,所以10 应该为这棵树的根,所以我们将10与4进行交换。
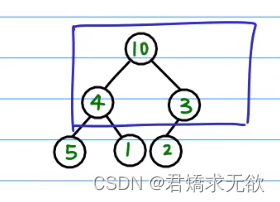
2、这时我们发现下面4为根的树又不满足条件了我们继续交换,这样我们将得到一个大根堆。
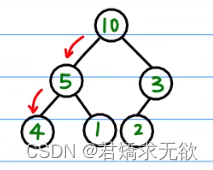
2.2、排序序列,将堆顶的元素值和尾部的元素交换
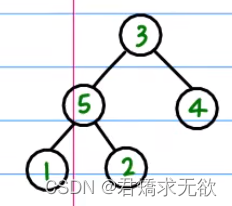
1、将最后一个元素与根顶交换(如图2);
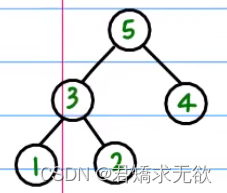
2、这时堆已经被打乱需要从新给根顶做交换,从新创建堆(如图3),此时需要创建堆的总个数应该减1;
3、如此反复操作1,2 步就可以排好序。
三、 代码及运行结果
#include <stdio.h>
void swap(int tree[], int i, int j)//传入需要交换两个数的下标
{
int temp;
temp = tree[i];
tree[i] = tree[j];
tree[j] = temp;
}
void heapify(int tree[], int num, int n)
{
int max = n;//假设根结点是最大的数
int left = n*2+1;//左孩子下标
int right = n*2+2;//右孩子下标
if(left < num && tree[left] > tree[max])//判断是否有左孩子以及是否大于根结点
{
max = left;
}
if(right < num && tree[right] > tree[max])//判断是否有由孩子以及是否大于根结点
{
max = right;
}
if(max != n)
{
swap(tree,n,max);//将最大的数与根结点交换
heapify(tree, num, max);//递归把最大数以下的树进行堆的排序
}
}
void build_heap(int tree[], int num)//从最后一个元素开始进行堆排序,创建堆
{
int parent = (num-1-1)/2;//最后一个元素父结点下标
int i;
for(i = parent; i>=0; i--)//从最后一个元素的父结点开始
{
heapify(tree,num, i);
}
}
void heapSort(int tree[], int num)
{
build_heap(tree, num);//先创建堆
int i=0;
for(i = num - 1; i > 0; i--)
{
swap(tree,i,0);//将最后一个元素与堆顶交换
heapify(tree, i, 0);//交换完后堆顶被破坏需要从新排序
//并且最大的数不能再次进入排序
//这里的i代表剩下需要排序的个数
}
}
int main(int argc, char *argv[])
{
int tree[] = {44, 17, 23, 79, 13, 53, 84, 8, 67, 33};
int num=sizeof(tree)/sizeof(tree[0]);//计算个数
heapSort(tree,num);
int i;
printf("排序后的结果为:\n");
for(i=0; i<num; i++)//打印排序后的结果
{
printf("%d ",tree[i]);
}
printf("\n");
return 0;
} 
四、复杂度分析
因为堆排序无关乎初始序列是否已经排序已经排序的状态,始终有两部分过程,构建初始的大顶堆的过程时间复杂度为O(n),交换及重建大顶堆的过程中,需要交换n-1次,重建大顶堆的过程根据完全二叉树的性质,[log2(n-1),log2(n-2)...1]逐步递减,近似为nlogn。所以它最好和最坏的情况时间复杂度都是O(nlogn),空间复杂度O(1)。