四元数与旋转矩阵之间的关系

在这里的旋转矩阵指的是坐标变换的旋转矩阵。

若矩阵与四元数均表示由坐标系G变换至用坐标系L进行表达。

则

因为某点P绕某轴旋转角后在坐标系中的坐标值，等于，保持点在空间中不动，将坐标系绕此轴旋转角度后，点在新坐标系中的坐标值。

而用四元数进行旋转操作时，是顺时针旋转为正方向。

假设坐标系G绕轴逆时针旋转角与坐标系L重合，则对应的四元数为

一、由四元数转换为坐标变换旋转矩阵的关系如下所示。经推导可得相互转换关系如下：(右乘)

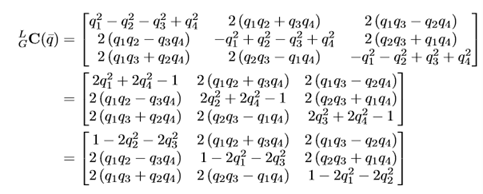
下面进行证明：

本旋转矩阵可以用Rodrigues' 旋转矩阵进行推导求证

罗德罗杰斯旋转矩阵如下。旋转轴方向单位矢量 ，旋转角度为。

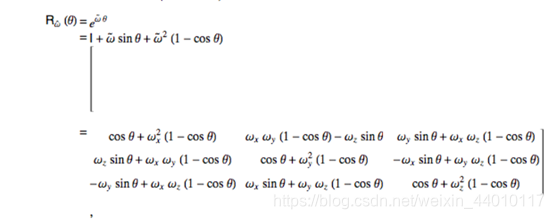
若采取左乘方式进行旋转，即，其中，与均为行向量。

则旋转效果是原点或图像绕旋转轴顺时针旋转角度。（左手螺旋法则）

若采取右乘方式进行旋转，即，其中，与均为行向量。

则旋转效果是原点或图像绕旋转轴逆时针旋转角度。（右手螺旋法则）

因为，所以若逆时针旋转角度，等于顺时针旋转角度，而，就等于把右乘变为左乘。

易证，，并且采取的右乘，所以效果等同于绕旋转轴逆时针旋转，而由坐标系关系博客可得几何变换与坐标系变换矩阵互逆，而我们可以证明

绕某轴旋转一定角度的矩阵与绕轴反向旋转的矩阵是互逆的，所以可以证明与q的关系的正确性。

二、由坐标变换旋转矩阵转换为四元数的方法如下所示：

设旋转矩阵T=

则的如下方程：

可得：

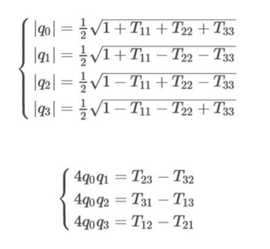
因为若绕轴旋转：

四元数的正负并不影响其的旋转效果。

相关链接：三维旋转：旋转矩阵，欧拉角，四元数 - 一叶斋主人 - 博客园

                   三维空间中的旋转：旋转矩阵、欧拉角 – Miskcoo's Space

                   旋转矩阵转化成四元数的三种算法 - CSDN博客