蒜头君的环状矩阵

题目：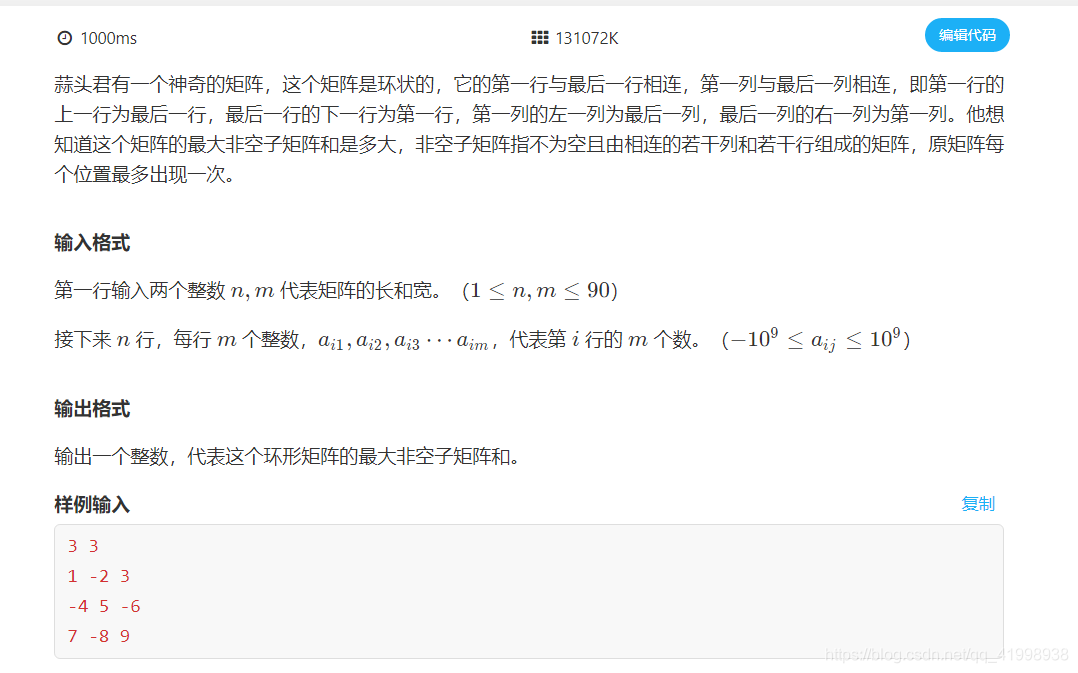


代码如下：

#include<bits/stdc++.h>
using namespace std;
#define NIL 1e9
long long a[405][405],pre[405][405];
int main()
{
	long long n,m,ans = -NIL,maxn,t;
	cin >> n >> m;
	for(int i = 1;i <= n;i++){
		for(int j = 0;j < m;j++){
			cin >> a[i][j];
			ans = max(ans,a[i][j]);
		}
	}
	if(ans < 0) cout << ans << endl;
	else{
		for(int i = 1;i <= n;i++)
			for(int j = 0;j < m;j++)
				pre[i][j] = pre[i - 1][j] + a[i][j]; //pre[i][j]代表第j列前i行总和
		for(int i = 1;i <= n;i++){
			for(int j = 1;j <= n;j++){	//这里与普通的矩阵不同，这里因为是环形矩阵所以从1开始 
				for(int k = 0;k < m;k++){
					maxn = 0;
					for(int l = 0;l < m;l++){
						if(i <= j) t = pre[j][(k + l) % m] - pre[i - 1][(k + l) % m]; //行不形成环 
						else t = pre[n][(k + l) % m] - pre[i - 1][(k + l) % m] + pre[j][(k + l) % m];//行形成环 
						if(t + maxn < 0) maxn = 0;
						else maxn += t;
						ans = max(maxn,ans);
					}
				}
			}
		}
		cout << ans << endl;
	}
	return 0;	
}

这道题是最大子矩阵和的一种变形，只要每次控制行的上下界，上界不一定要比下界小，因为此处时环形的。列也是同样道理。