前言

湖北新增一万多例中，大多数是临床病例，而真正的确诊病例，却只有两千多一点，比昨天略低。（关于临床病例和确诊病例的区别，请点击这里。）

不过不论如何，确诊人数数据由于临时加上临床诊断病例，导致目前没法用来做模型预测。现在能用来做预测的，只有 疑似病例 人数数据。

下面，我们将用疑似病例数据来做预测。原因如下：

• 临床诊断将计入确认人数，这就意味着确认病例人数受到干扰，而且干扰的程度非常大~
• 确诊病例来源于疑似病例。在《新型冠状病毒感染的肺炎诊疗方案（试行第五版）》中，在湖北省的病例诊断分类中增加了“临床诊断”，临床诊断来源于疑似病例，确诊病例来源于临床诊断和疑似病例。
• 确诊病例在诊断过程受到硬件条件(如核酸试剂的数量、其他医疗设备的数量)的限制，遗漏的人数应该较多；而疑似病例判断标准则较低，只要其流行病史和是否发热等，遗漏的人数应该较少。

因此，我们将会用疑似病例来进行后续预测。

步骤一：抓取数据

从腾讯实时疫情数据，我们抓取 每日增加 数据，抓取结果如下：

    date  confirm  suspect  dead  heal  deadRate  healRate
0    1.2       77       27     0     0       0.0       0.0
1   1.21      149       53     3     0       2.0       0.0
2   1.22      131      257     8     0       6.1       0.0
3   1.23      259      680     8     6       3.1       2.3
4   1.24      444     1118    16     3       3.6       0.7
5   1.25      688     1309    15    11       2.2       1.6
6   1.26      769     3806    24     2       3.1       0.3
7   1.27     1771     2077    26     9       1.5       0.5
8   1.28     1459     3248    26    43       1.8       2.9
9   1.29     1737     4148    38    21       2.2       1.2
10   1.3     1982     4812    43    47       2.2       2.4
11  1.31     2102     5019    46    72       2.2       3.4
12  2.01     2590     4562    45    85       1.7       3.3
13  2.02     2829     5173    57   147       2.0       5.2
14  2.03     3235     5072    64   157       2.0       4.9
15  2.04     3893     3971    65   262       1.7       6.7
16  2.05     3697     5328    73   261       2.0       7.1
17  2.06     3143     4833    73   387       2.3      12.3
18  2.07     3401     4214    86   510       2.5      15.0
19  2.08     2656     3916    89   600       3.4      22.6
20  2.09     3062     4008    97   632       3.2      20.6
21   2.1     2484     3536   108   716       4.3      28.8
22  2.11     2022     3342    97   744       4.8      36.8

附抓取代码（类似过程可见《新型冠状病毒数据抓取及整理详细流程》）：

import json
import pandas as pd
import numpy as np
from datetime import datetime
# 这里requests-html需要python3.5以上版本
from requests_html import HTMLSession

# 创建会话
session = HTMLSession();
url = r'https://view.inews.qq.com/g2/getOnsInfo?name=disease_h5';
# 从目标网址中读取数据
r = session.get(url).json();
# 将数据存储为json格式
data = json.loads(r['data']);
# 每日新增数据（将'date'列排在第一列）
chinaDayAddData = pd.DataFrame(data['chinaDayAddList'])[['date', 'confirm', 'suspect', 'dead', 'heal', 'deadRate', 'healRate']];
# 保存
chinaDayAddData.to_csv(r'F:\开课吧\RS基础课\2019_CoV_chinaDayAddData.csv', encoding='gbk', index=None)
# 读取
chinaDayAddData = pd.read_csv(r'F:\开课吧\RS基础课\2019_CoV_chinaDayAddData.csv', encoding='gbk');
chinaDayAddData['date'] = chinaDayAddData['date'].map(str);

步骤二：估计实际确诊人数

我们要做以下事情：

• 估计疑似病例中确诊的比例
• 根据每日增加数据确定确诊人数
• 根据SI模型，确定最终确诊人数、疫情结束的大概时间

我们首先看如何通过现有数据，估计疑似病例中确诊比例。

# 最小二乘法
# 采样点
# 确诊病例每日增加数
Yi = np.array(list(chinaDayAddData['confirm']));
# 疑似病例每日增加数
Xi = np.array(list(chinaDayAddData['suspect']));

# 需要拟合的函数func及误差error
def func(p, x):
    return p * x;

def error(p, x, y):
    return func(p, x) - y;

# 疑似病例确诊比例的初始值
p0 = 0.5;
# 最小二乘法做出的疑似转确诊比例
percent = leastsq(error, p0, args=(Xi, Yi))[0][0];
print(percent);

这样得到的疑似转确诊比例为0.5960971132108407。

其次，我们根据每日增加的每日疑似病例增加数据确定确诊人数。

• 确定每日疑似病例总数，我们需要累加和函数cumsum()
• 确定每日确诊病例总数，我们只需将0.5960971132108407乘以每日疑似病例总数

代码如下：

predict = chinaDayAddData['suspect'].cumsum() * 0.6

我们将现在作出的预测与官方给出的每日确诊人数进行比较，如下：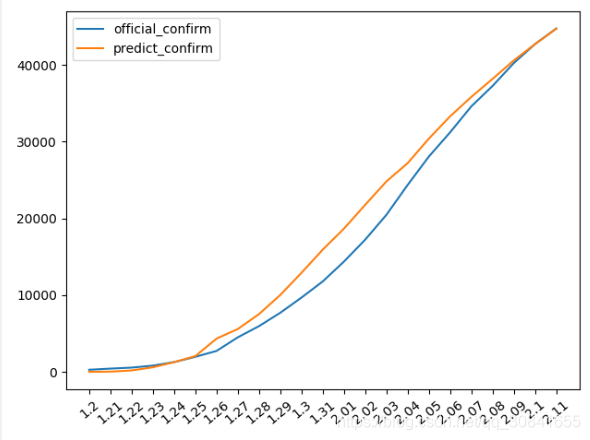

可见，我们预测的每日确诊病例总数要比官方给出的要高，但是最近几天开始重合。这其实可以这样理解，在当前国家高度重视和充分宣传之下，个人和各级政府不再存在瞒报，因此可以认为是真实数据。

退一万步，如果所有疑似病例都转变成确诊病例，那么如绿线所示，当前的实际感染总人数为7万多人~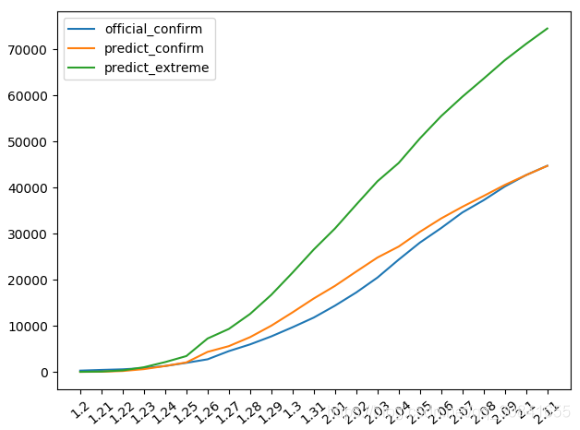

步骤三：预测

这里，我们选择SI模型。在说明选择这个最简单模型之前，先给一个简介。

SI模型

在这个最简单的传染病模型中，我们仅仅考虑健康人（即易感者，Susceptibles）和病人（即感染者，Infection）。

我们作出如下假设：

• 总人数$N$不变，病人和健康人的比例分别为$i(t)$和$s(t)$。其中，$t$为从0开始的时间，以天为单位。
• 每个病人每天接触到的人数为$\lambda$，且能使得其中的健康人感染。

根据上述假设，我们可以列出下式：
$$N\cdot [i(t+\Delta t)-i(t)]=\lambda s(t)\cdot Ni(t)\Delta t$$
经过简单的变形，我们有
$$\frac{di}{dt}=\lambda si$$
且根据假设，
$$i+s=1$$
因此，我们可以写出微分方程，如下
$$\{\begin{array}{lll}\frac{di}{dt}& =& \lambda i(1-i)\\ i(0)& =& i_0\end{array}$$
其中，$i(0)=i_0$为初始条件。

求解上述微分方程，可以得到Logistic模型，即
$$\begin{array}{lll}i(t)& =& \frac{1}{1+\left(\frac{1}{i_0}-1\right)e^{-\lambda t}}\\ & =& \frac{i_0{e}^{\lambda t}}{i_0(e^{\lambda t}-1)+1}\end{array}$$

但通过观察这个公式，我们发现，随着时间$t$的增加，感染比例$i(t)$也逐渐增加，最后趋近于1。这就意味着最后所有人都会被感染。

说明

可以反向思考，在疫情结束之后看现在，有什么特点呢？

• 假设整个疫情造成的确诊人数为$N$；
• 当前这$N$个人中，我们假设确诊比例为$i(t)$，尚且健康的人的比例为$s(t)$；
• 在这一过程中，确诊比例不断增大，且存在斜率先增加后减少的过程；
• 最终$i=1,s=0$。

SI模型预测

我们用SI模型根据估计的确诊人数进行预测。我们需要估计三个参数$N,i_0,\lambda$。

# 采样点
Yi = np.array(predict);
Xi = np.arange(len(Yi));

# Logistic模型
def i_t(t, i0, lamb):
    i1 = i0 * math.exp(lamb * t);
    return i1 / (1 + i1 + i0);

# 需要拟合的函数func及误差error
def func(p, x):
    i0, N, lamb = p;
    y = np.array([i_t(t, i0, lamb) * N for t in x]);
    return y

def error(p, x, y):
    return func(p, x) - y;

p0 = [0.01, 1000, 1];
#print(func(p0, Xi))
#print(error(p0, Xi, Yi));
Para = leastsq(error, p0, args=(Xi,Yi));
print(Para);

这样得到的值为$(i_0,N,\lambda )=(1.88087189e-02,4.72770019e+04,2.90671789e-01)$。

将这样的值代入原方程，我们可以作出

# 预测1月20号之后40天的确诊人数的状况
Xi = np.arange(40);
y_fit = func(Para[0], Xi);
plt.plot(Xi, y_fit, label=r'predict_confirm');
#plt.plot(Xi, Yi, label=r'original');
plt.legend();
plt.show();

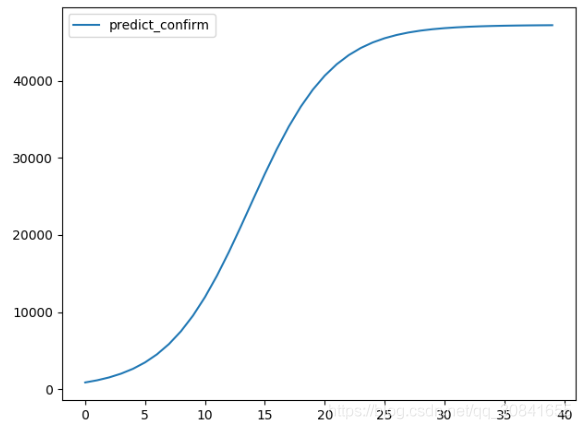
即，在3月中旬左右疫情不会再大量增加，同时，最终确诊总人数为47277人。

同样，我们退一万步说，疑似病例全部确诊为确诊病例，这样，我们有

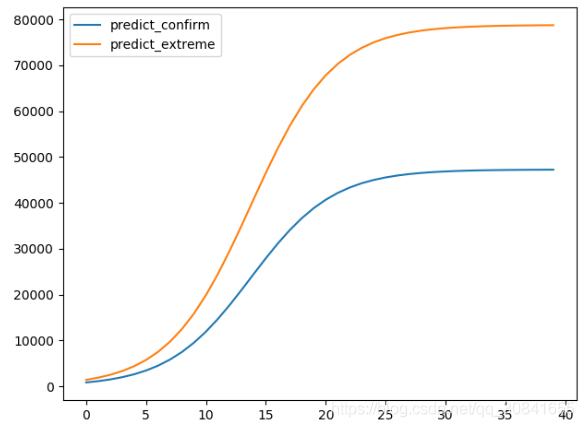
在极端情况（所有疑似病例最终都确诊为新冠肺炎）下，最终确诊总人数为78744，同样在3月中旬左右结束。