分析二叉树遍历的性质

根据后序和中序遍历输出先序遍历：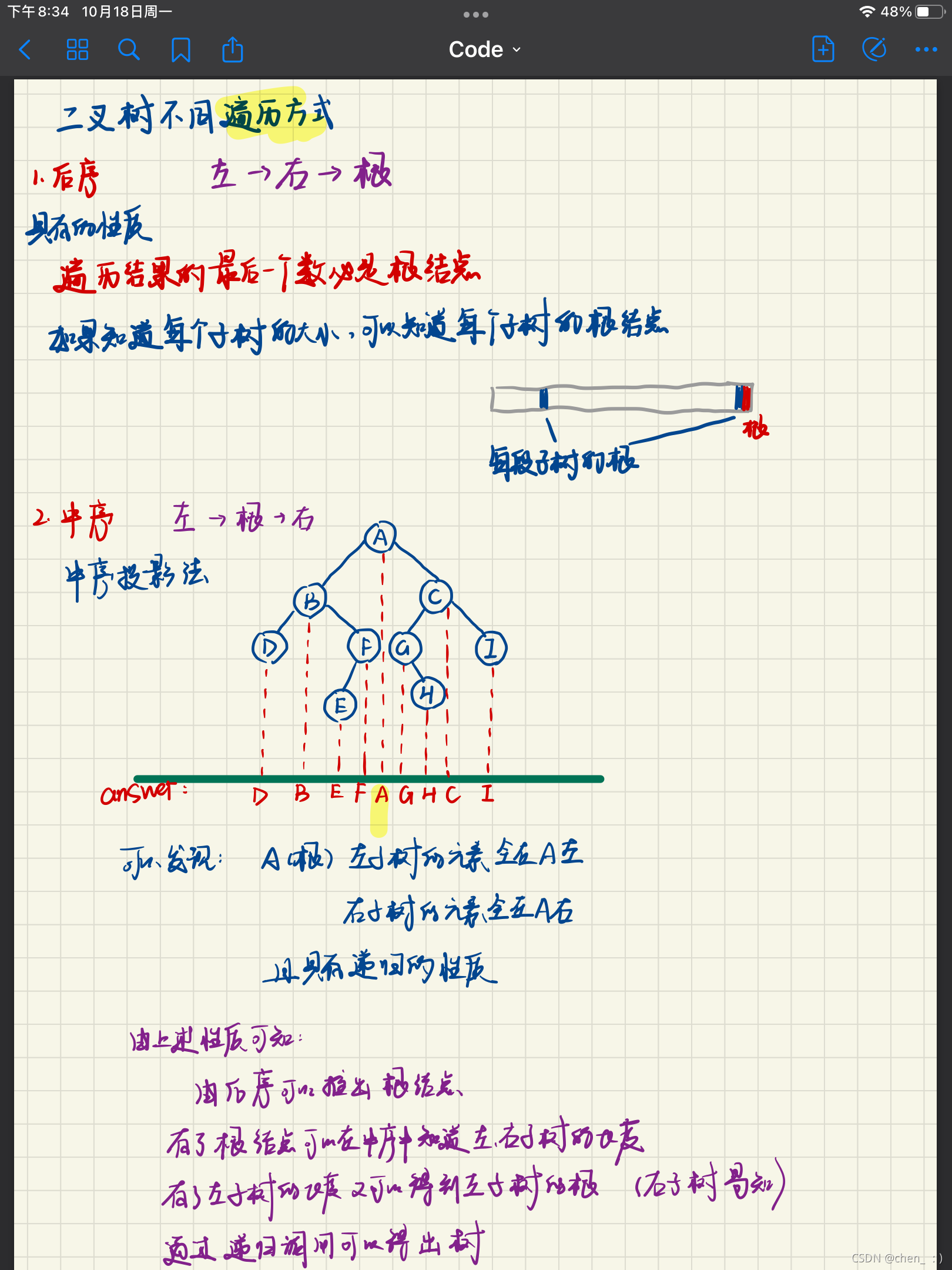

由上述性质，易做：

题目

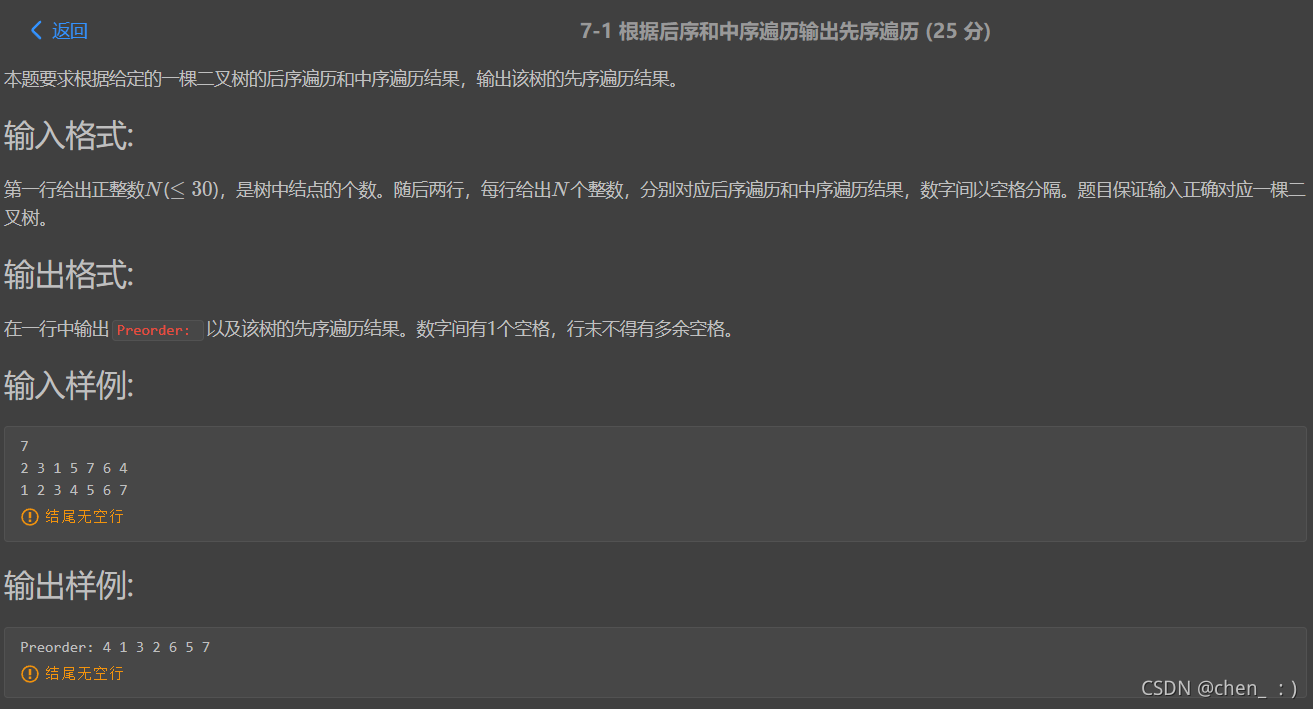
code：

#include<iostream>
using namespace std;
const int N = 110;

void make_a(int *c,int *b,int n){
         if(n == 0) return;  
         int x = c[n-1];
         int i;
         for(i=0;i<n;i++)
               if(b[i] == x) break;
         cout << " " << x;
         make_a(c,b,i);
         make_a(c+i,b+i+1,n-i-1);   // 后缀是从c+i开始，是因为后缀删除的根节点是最后一个节点，并不是第i个节点，所以后缀时仍要用第i个节点，但是不需要用最后一个节点
                                    // 中缀要把第i个结点删除，所以中缀表达式是从i+1个元素开始的；（即后缀每次删最后元素，中缀删掉是中间元素）
}

int main(){
    int b[N],c[N];  // b->中缀    c->后缀
    int n;
    cin >> n;
    for(int i=0;i<n;i++)
        cin >> c[i];
    for(int i=0;i<n;i++)
        cin >> b[i];
    cout << "Preorder:";
    make_a(c,b,n);
    return 0;
}

attention：

分析后缀、中缀有差别（因为元素的位置不同）
后缀是从第i个元素（即元素c+i）开始，是因为后缀删除的根节点是最后一个节点，并不是第i个节点，所以后缀时仍要用第i个节点，但是不需要用最后一个节点
中缀要把第i个结点删除，所以中缀表达式是从i+1个元素（即元素b+i+1）开始的；（即后缀每次删最后元素，中缀删掉是中间元素）

ps

补充：树的计数

已知先序序列和中序序列可确定一棵唯一的二叉树；

已知后序序列和中序序列可确定一棵唯一的二叉树；

已知先序序列和后序序列不能确定一棵唯一的二叉树。

improve： 根据前序和中序遍历输出先序遍历 -> 传送门