【算法】矩阵的最小路径和

题目

给定一个矩阵，从矩阵左上角开始走到右下角，每次只能向下或向右，将路径上的数字求和，求所有路径中路径和最小的。

举例

给定矩阵：

最短路径如下：

解答

1.假设现在给定1*4的矩阵R：

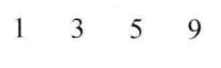
设当前元素距离左上角的距离为dp[0][i]，那么矩阵R的dp[0]如下：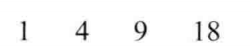

则最小路径和为18

2.假设现在给定4*1的矩阵C：

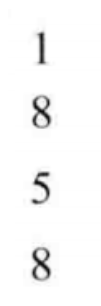
设当前元素距离左上角的距离为dp[i][0]，那么矩阵R的dp[i][0]如下：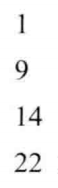

则最小路径和为22

3.假设现在给定4*4的矩阵M：

根据情况1、2很容易写出第一行和第一列的dp值，如下：

此时很容易计算出左上角到达任意位置的最短路径和
例如从左上角到第2行第2列（从1开始计数）的最小路径和，只需取该元素的上面和左边元素的最小路径和与自己的值相加即可
易得状态转移方程：dp[i][j] = min(dp[i-1][j],dp[i][j-1])+M[i][j]
求出dp如下：

则最小路径和为12

代码

public class Main {
    static Scanner in = new Scanner( System.in );
    public static void main(String[] args) {
        int row = in.nextInt();
        int col = in.nextInt();
        int[][] m = new int[row][col];
        int[][] dp = new int[row][col];
        dp[0][0] = m[0][0];
        for (int i = 1; i < col; i++) {
            dp[0][i] = dp[0][i-1] + m[0][i];
        }
        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i-1][0] + m[i][0];
        }
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min( dp[i-1][j],dp[i][j-1] )+m[i][j];
            }
        }
    }
}