1.头文件及类型定义

#include<stdio.h>
#include<stdlib.h>
#define ElemType char

2.线索二叉树结点类型定义

//线索二叉树结点类型定义
typedef struct ThreadNode {
	ElemType data;							//数据元素
	struct ThreadNode* lchild, * rchild;	//左、右孩子指针
	int ltag, rtag;							//左、右线索标志
	//tag=0,表示指针指向孩子;tag=1,表示指针是“线索”,ltag指向前驱，rtag指向后继
}ThreadNode, * ThreadTree;

3.函数声明

/*函数声明*/
void CreateThTree(ThreadTree& T);			//1.先序建立线索二叉树
void InitThread(ThreadTree& T);				//2.初始化tag
void visit1(ThreadNode* q);					//3-1.访问并建立线索
void PostThread(ThreadTree T);				//3-2.遍历
void CreatePostThread(ThreadTree T);		//3-3.后序线索化主过程
ThreadNode* PreNode(ThreadNode* p);			//4.找到p的前驱结点
void visit2(ThreadNode* p);					//5-1.打印结点
void RevPostOrder(ThreadNode* T);			//5-2.利用后序前驱实现逆向后序遍历

4.基本操作

4.1 先序建立线索二叉树

/*1.先序建立线索二叉树*/
void CreateThTree(ThreadTree& T) {
	char c;
	scanf("%c", &c);
	if (c == '#')
		T = NULL;
	else {
		T = (ThreadNode*)malloc(sizeof(ThreadNode));
		T->data = c;
		CreateThTree(T->lchild);
		CreateThTree(T->rchild);
	}
}

4.2 初始化tag

/*2.初始化tag*/
void InitThread(ThreadTree& T) {
	if (T != NULL) {
		T->ltag = 0;
		T->rtag = 0;	//初始化当前树中的tag指针为0，表示还未线索化
		InitThread(T->lchild);	//递归遍历左子树
		InitThread(T->rchild);	//递归遍历右子树
	}
}

4.3 后序线索化二叉树

4.3.1 访问并建立线索

ThreadNode* pre = NULL;		//pre指向当前访问结点的前驱
//3-1.访问并建立线索
void visit1(ThreadNode* q) {
	if (q->lchild == NULL) {	//左子树为空，建立前驱线索
		q->lchild = pre;
		q->ltag = 1;
	}
	if (pre != NULL && pre->rchild == NULL) {	
		pre->rchild = q;	//建立前驱结点的后继线索
		pre->rtag = 1;
	}
	pre = q;			//标记当前结点为刚刚访问过的结点
}

4.3.2 遍历

//3-2.遍历
void PostThread(ThreadTree T) {
	if (T != NULL) {
		PostThread(T->lchild);	//后序遍历左子树
		PostThread(T->rchild);	//后序遍历右子树
		visit1(T);				//访问根节点
	}
}

4.3.3 后序线索化主过程

//3-3.主过程
void CreatePostThread(ThreadTree T) {
	pre = NULL;			//pre初始化为NULL
	if (T != NULL) {	//非空二叉树才能线索化			
		PostThread(T);	//后序线索化二叉树
		if (pre->rchild == NULL)	
			pre->rtag = 1;			//处理遍历的最后一个结点
	}
}

4.4 寻找后序前驱

//4.寻找后序前驱
ThreadNode* PreNode(ThreadNode* p) {
	if (p->ltag == 0) {		//若ltag=0，说明所找结点有左孩子
		if (p->rtag == 0)		//若rtag=0
			return p->rchild;		//说明所找结点有右孩子，根据后序遍历的特点(左-右-根)，右孩子为前驱
		else                    //若rtag=1
			return	p->lchild;		//说明所找结点无右孩子，则前驱结点为其左孩子
	}
	else
		return p->lchild;	//若ltag=1，说明所找结点无左孩子，则返回前驱线索
}

4.5 逆向后序遍历

4.5.1 打印结点

//5-1.打印结点
void visit2(ThreadNode* p) {
	printf("%c\t", p->data);
}

4.5.2 利用后序前驱实现逆向后序遍历

//5-2.利用后序前驱实现逆向后序遍历：空间复杂度为O(1) 
void RevPostOrder(ThreadNode* T) {
	for (ThreadNode* p = T; p != NULL; p = PreNode(p))
		visit2(p);
}

4.6 main函数

int main() {
	ThreadTree T;

	/*1、创建二叉树*/
	printf("先序创建二叉树：");
	CreateThTree(T);

	/*2、初始化tag为0*/
	InitThread(T);

	/*3、后序线索化*/
	CreatePostThread(T);

	/*4、寻找后序前驱（用根结点测试）*/
	printf("根结点的后序前驱为：%c\n", PreNode(T)->data);

	/*6、逆向后序遍历二叉树*/
	printf("<————逆向后序遍历————>\n");
	RevPostOrder(T);

	return 0;
}

4.7 测试

4.7.1 二叉树结构

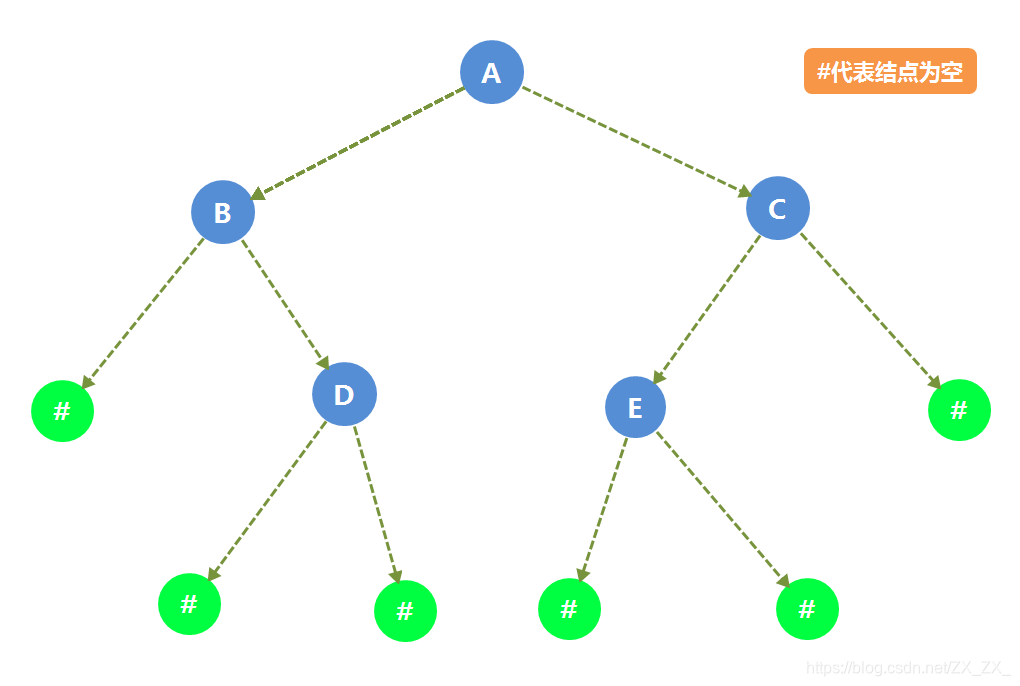
4.7.2 测试结果

5.小结

• 对于后序线索二叉树并不会出现“转圈"现象，原因是根结点是最后被访问的，不可能再回去访问其左右孩子指向的子树。
• 另外，同先序线索二叉树一样，后序线索二叉树也存在类似的问题：即只能找到后序前驱。具体分析同先序线索二叉树类似，已在上一篇文章小结中介绍，此处不再展开。