[蓝桥杯 2018 省 AB] 全球变暖（BFS/DFS）

 题目传送门

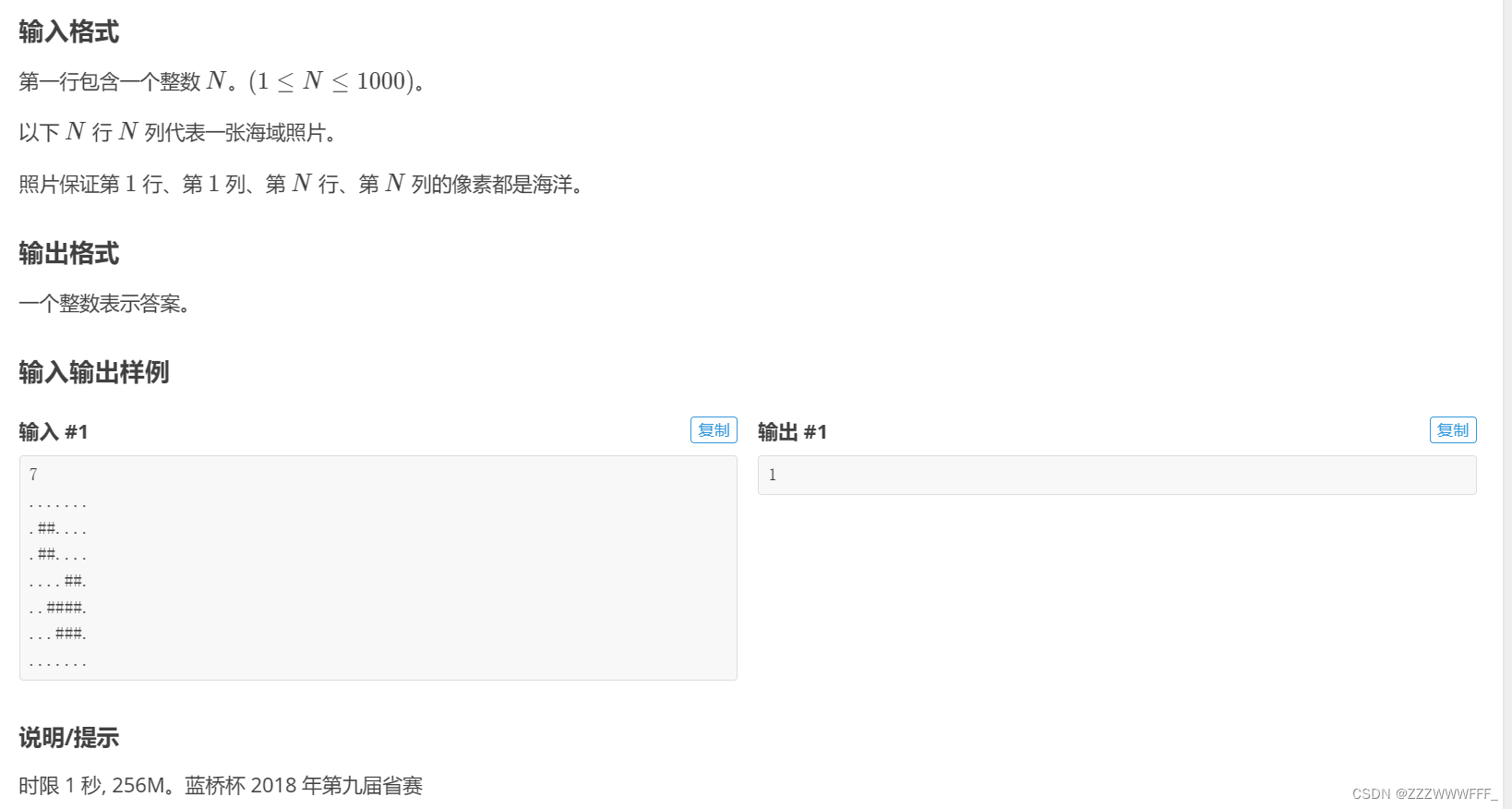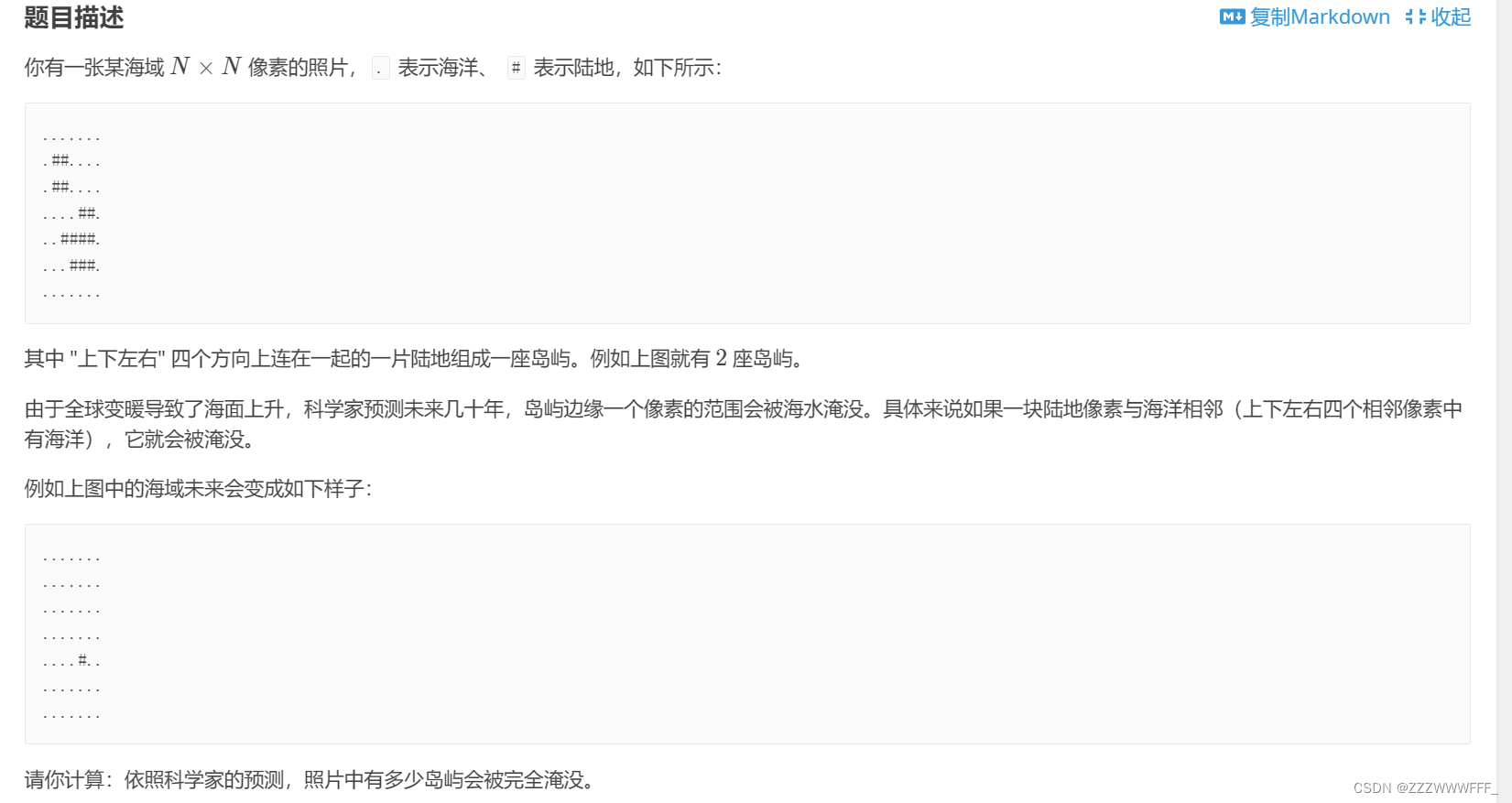
 题目上要注意的主要是：这里是求被完全淹没的岛屿数量！！！

思路1：

这里我的第一思路是先使用搜索求（BFS/DFS）出所有的岛屿数量，同时在搜索过程中标记所有会被淹没的陆地的下标，搜索完毕后再把这些下标的陆地都变成海洋，再搜索整个图有多少个岛屿，最后前后求出的岛屿数相减就是答案

看着这思路是不是很清晰，以为能AC？？

错了，这里存在一个问题，是海洋有可能将未被淹没的岛屿给分隔开，即可能增加岛屿数量

例如：

7
.......
.##.##.
.#####.
.##.##.
.......
...##..
.......

如上图，如果按照我上面的思路会输出0，实际上应该输出1

于是我决定反过来

思路2：

我们上面的思路是找到被淹没的陆地，下面也可以找到不会被淹没的陆地

每次搜索岛屿时，检查是否存在上下左右都是陆地的元素，如果存在，那么这个岛屿就不会被淹没，计数，最后用原来的岛屿数减去不会被淹没的岛屿即可

这样就避免了上面的问题

#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
#define MAX 1010
using namespace std;

int n, ans=0,sign;
bool visited[MAX][MAX];
int nextt[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };
char map[MAX][MAX];

bool check(int x, int y) {//如果存在不会被淹没的（x,y）就返回true，反之返回false
	for (int i = 0; i < 4; i++) {
		int tx = x + nextt[i][0];
		int ty = y + nextt[i][1];
		if (map[tx][ty] == '.') {
			return false;
		}
	}
	return true;
}

void bfs(int x, int y) {
	queue<pair<int, int> >q;
	q.push({ x,y });
	visited[x][y] = true;

	while (!q.empty()) {
		x = q.front().first;
		y = q.front().second;
		q.pop();
		if (check(x, y)) {
			sign = 1;
		}
		for (int k = 0; k < 4; k++) {
			int tx = x + nextt[k][0];
			int ty = y + nextt[k][1];
			if (map[tx][ty] == '.' || visited[tx][ty]) {
				continue;
			}
			visited[tx][ty] = true;
			q.push({ tx,ty });
		}
	}
}


int main()
{
	int num = 0;
	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> map[i][j];
		}
	}
	memset(visited, false, sizeof(visited));
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (!visited[i][j] && map[i][j] == '#') {
				num++;//原来的岛屿总数
				sign = 0;
				bfs(i, j);
				if (sign == 1) {
					ans++;//不会被淹没的岛屿数
				}
			}
		}
	}
	cout << num-ans << endl;
	return 0;
}
//7
//.......
//.##.##.
//.#####.
//.##.##.
//.......
//...##..
//.......