假币称重：汉明纠错码的应用

这是一道经典的信息论题目，存在不唯一的最优解。大部分参考书中似乎都没有给出一般性（任意数量的假币）的解决方案，本模型的结果正确性有待考究。
完整代码查看 github

问题描述

设有 $n$ 枚硬币，其中仅有一枚假币，在已知或未知假币与真比之间重量关系两种情况下 ，通过无砝码天平称重的方法鉴别假币，求所需的最少称重次数。要求：

1. 试用信息论的原理进行分析，并给出 $n=12,39$ 的具体称重策略；
2. 编程实现可视化。

emmm，这里的可视化是指用图表表示出称重策略就好了还是要画出天平，托盘呢 ?

称重次数下界

使用无砝码天平进行称重只可能有三种结果（左盘重，等重，右盘重）。则每称重一次最多可以获得（等概情形）的信息量为

$$I={\log }_{2}3\text{bits}$$

假设所有硬币中出现假币是等可能的，若已知假币较真币要轻，则对于硬币来说一共有 $n+1$ 种可能状态，即其中某一个硬币较轻或者它们一样重。此时的熵为 ${\log }_2(n+1)$ ，则通过称重的方式获知哪一块是假币需要的次数

$$k\ge \frac{{\log }_2(n+1)}{{\log }_{2}3}={\log }_3(n+1)$$

而若事先不知道假币是轻还是重，则一共有 $2n+1$ 种状态，此时最少称重次数为

$$k_{\min }=\lceil {\log }_3(2n+1)\rceil$$

其中 $\lceil \cdot \rceil$ 为向上取整符号。下图给出了是否已知假币轻重对称重次数下界的影响。

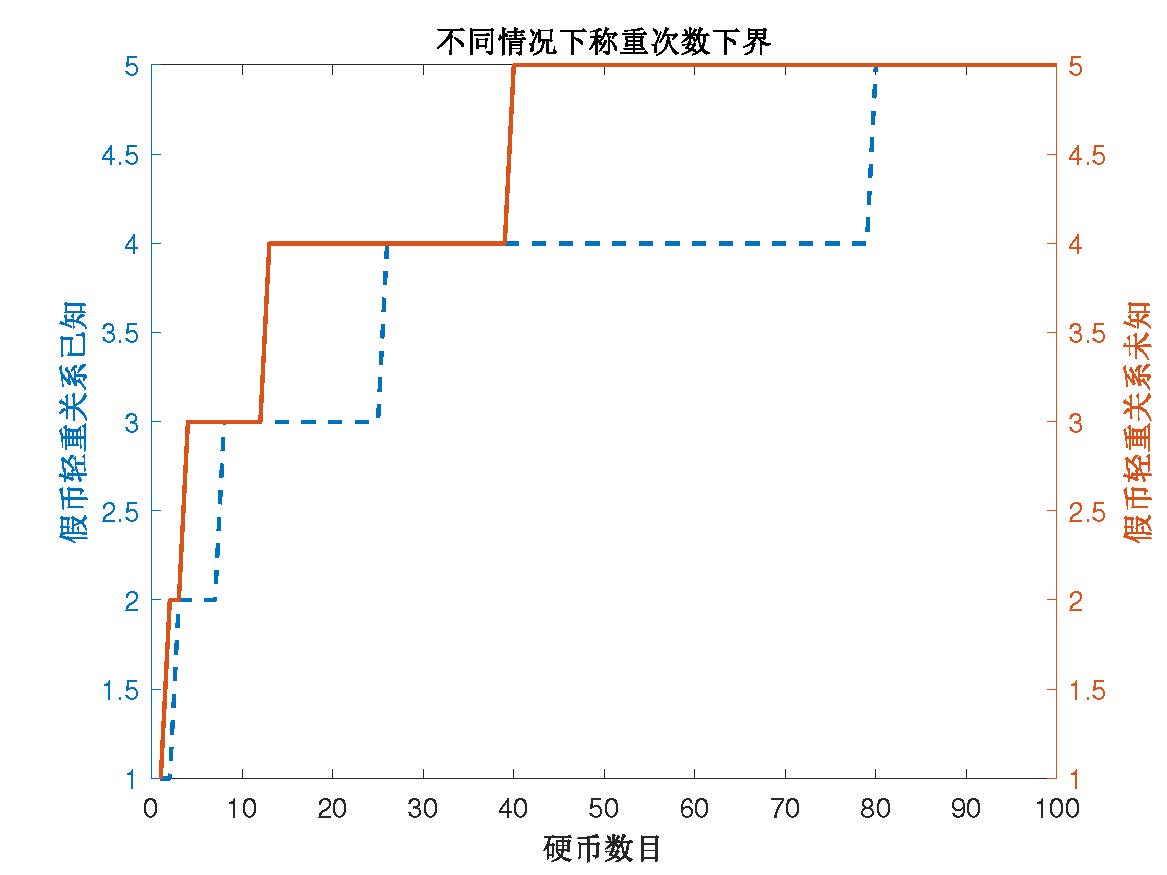
由图可知已知假币与真币轻重关系在大部分情况下具有更低的称重次数下界。但是一般情况下应该不知道假币与真币轻重关系，下面主要讨论这种情形。

事实上已知轻重时可以用类似下面的方法给出最优策略，但是为达到称重次数下界需要的搜索量似乎更大

以上确定了称重次数的下界，但是如何设置称重策略来达到这个下界呢？下面参考信号纠错的思想构造性的给出一种最优策略 。

汉明纠错码

汉明纠错码是一种线性分组码，可以用来恢复特定情况下某一位发生变异的信号 。而唯一的假币正是相当于发生了变异的真币。而且汉明码是完备码，它在于分组长度相同、最小距离为 3 的码中能达到最高的码率。

1. 编码的距离一般只两个编码不同元素的最大个数。

2. Todd K Moon. Error correction coding. Mathematical Methods and Algorithms. Jhon Wiley and Son, pages 2001–2006, 2005.

汉明码纠错主要应用了线性变换的零空间概念 。

已本题为例，取硬币为 12 枚，只需要称三次便可以找到假币。而长度为 3 的码要表示 12 种以上数字至少是 3 进制。故而可对 1-12 号硬币进行如下编码

$$H=\left[\begin{array}{llllllllllll}0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 1\\ 0& 0& 1& 1& 1& 2& 2& 2& 0& 0& 0& 1\\ 1& 2& 0& 1& 2& 0& 1& 2& 0& 1& 2& 0\end{array}\right]$$

其中 $H$ 通常称为奇偶校验矩阵（parity check matrix）。易知矩阵 $H$ 的秩 $rank(H)=3$（即这种编码的最大汉明距离也为 3），从而其零空间的维度为

$$\dim (Ker(H))=12-rank(H)=9$$

这意味着存在 $2^9$ 个 $12\times 1$ 的向量 $\mathbf{c}$ 使得

$$\mathbf{H}\mathbf{c}=0$$

这些所有的向量 $\mathbf{c}$ 便可以作为信息发送出去，而且若其中某一个位置上元素发生了改变可以通过以下途径快速辨识出是哪个位置发生了错误：

设发出信息为 $\mathbf{c}$（$\mathbf{c}$ 必须属于 $H$ 的零空间），而位置 $i$ 发生了变异（对应本题中的假币序号），收到的信息为 $\mathbf{r}=\mathbf{c}+{\mathbf{e}}_i$，其中 ${\mathbf{e}}_i$ 表示仅第 $i$ 个位置为 1 ，其余地方为零。从而

$$\mathbf{H}\mathbf{r}=\mathbf{H}(\mathbf{c}+{\mathbf{e}}_i)=\mathbf{H}{\mathbf{e}}_i$$

而 $\mathbf{H}{\mathbf{e}}_i$ 表示矩阵 $H$ 的第 $i$ 列。故而只需要对收到的信息做一次矩阵乘法再去矩阵内进行匹配便可知道变异位置，从而找到假币。

假币称重最优策略

但是上述模型并不能直接应用过来，因为接受信息 $\mathbf{r}$ 在这里并不能量化成假币的质量，我们只能通过天平比较不同数量的硬币质量。故而需对编码方式进行修改，将三进制的基改为 $\{-1,0,1\}$ ，则可以用 $-1$ 表示将硬币放在左盘，$0$ 表示将硬币搁置一旁，$1$ 表示放在右盘。

用 $\mathbf{c}=(0,0,\cdots ,0)$ （零向量必然属于 $\mathbf{H}$ 的零空间）表示没有假币的情形，有假币则是在某一个位置将 0 变成 1（此时假币重） 或者 -1（此时假币轻）。编码后结果如下图所示。

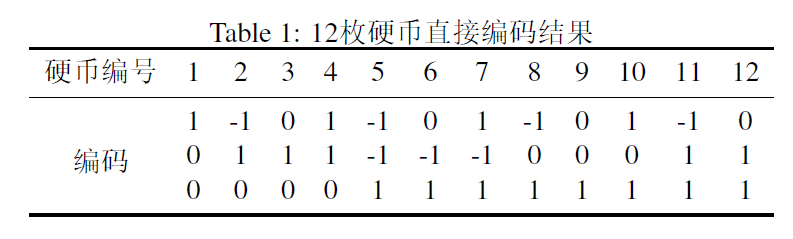
将硬币编码为上述三进制的代码如下：

function y = ternary(num,length)
k = 3;
now = num;
for i=1:length-1
    if mod(now,3^i) / 3^(i-1)==2  % Equivalent to -1
        y(i) = -1 ;
    else
        y(i) = mod(now,3^i) / 3^(i-1);
    end
    now = now - y(i)*3^(i-1);
end
y(length) = now / 3^(length-1);
y = y';
end

但是使用天平必须左右摆放的硬币数目一致，故而需要使得上图中编码结果每一行的 -1 的数目等于 1 的数目，只需要将部分硬币的编码乘以 -1 即可（并不会改变矩阵的秩）。由于每一个硬币的编码都有可能被要求变为相反数，故而一共需要编码 $2n+1$ 种状态，编码长度即 $k=\lceil {\log }_3(2n+1)\rceil$ 恰好达到称重次数的下界。

对上述编码进行调整的方案有很多，不同的方案可以得到不同的最优策略。亦即本问题的最优策略不唯一，对哪些硬币进行调整这是一个组合搜索问题，当硬币数较多时是 NP Hard 的，这里采用遗传算法进行搜索。损失函数定义如下

设变量 $x_i$ 表示是否将第 $i$ 号硬币的编码变为其相反数。设原来的编码矩阵为 $R_{k\times n}$ ,对于每一轮称重 -1 和 1的数目相等相当于编码的和为零。故而转化为一下优化问题

$$\begin{gathered} \underset{\mathbf{x}}{\min }\sum _{j=1}^k\sum _{i=1}^n{x}_i{R}_{ji} \\ {x}_i=-1,1i=1,2,\cdots ,n \end{gathered}$$

遗传算法调整编码

39 枚硬币最优策略搜索过程示意如下图所示

其中12 枚硬币的一种调整方式如下图所示

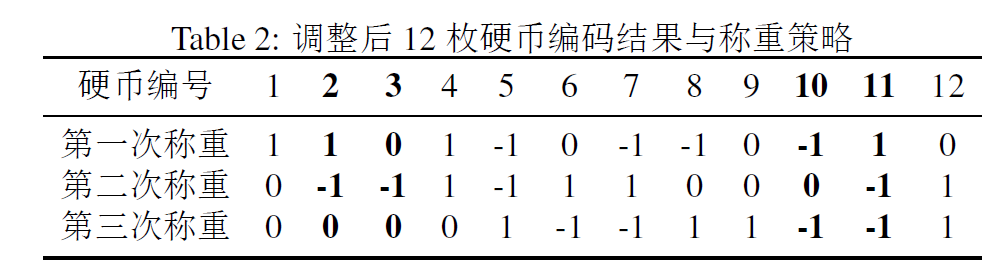
加粗的编码表示较原先进行了调整。39 枚硬币的称重策略可视化为下图

其中黑色表示放在左盘，白色表示放在右盘。

确定假币位置与轻重

至此上述编码不仅符合汉明纠错码的性质，而且给出了硬币的称重策略。由汉明纠错码知假币位置可唯一确定。那如何判断轻重呢？每一次称重结果若为左盘重，记编码 -1，若两边等重，记编码 0 ，若左盘轻则记 1。最后将此编码反译为硬币编号，则对应编号的硬币为假币。并且若编码和原编码匹配，则说明假币较重；若为原编码的相反数，则说明假币较轻。比如最后得到 $-1,0,-1$ ，则假币为 $-1\times 3^0+0\times 3^2-1\times 3^2=-10$ ，即 10 号为假币，且得到的序列与上图中编码序列相同，故而10号为假币，且较真币更重。