排序算法——冒泡、插入、选择

冒泡排序

冒泡排序只比较相邻两个元素之间的大小，如果元素大小关系不正确，则交换这两个数，重复该步骤，直到我们到达数组的末尾。
一次冒泡至少让一个元素处于正确位置，重复n次冒泡，则完成了n个元素的排序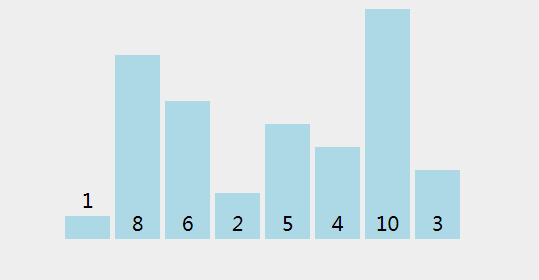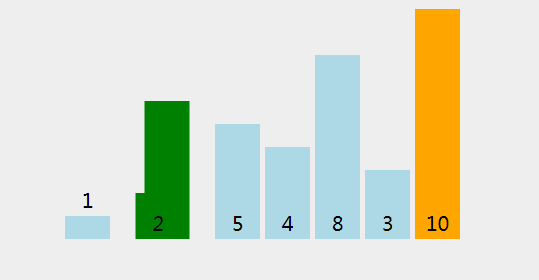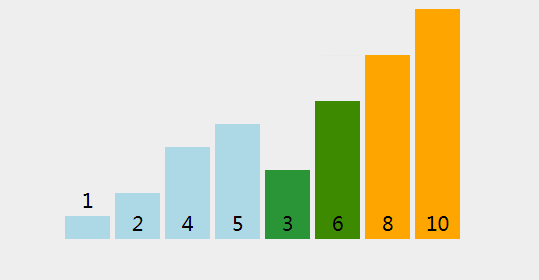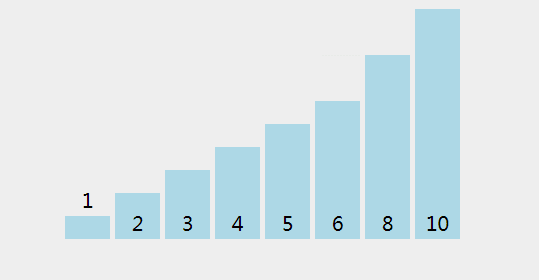

冒泡排序也能进行优化
改进的思路很简单：如果我们通过内部循环完全不交换，这意味着数组已经排序，我们可以在这个点上停止冒泡排序。

public static void bubblesort(int[] a) {
    int n = a.length;
    if (n<=1) return;


    int temp;
    for (int i = 1; i < n; i++) {
        boolean flag = false;//判断数据交换的标志
        for (int j = 0; j < n-i-1; j++) {
            if (a[j] > a[j + 1]) {//进行交换
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                flag=true;//有数据交换
            }
        }
        if (flag==false)
            break;//如果没有数据交换，则退出循环
    }
}

冒泡排序的时间复杂度
最好时间复杂度：O（n）：即数组已经有序，只需要一次冒泡操作
最坏时间复杂度：O（n²）：即数组逆序，则需要n次冒泡操作，则交换次数为n(n-1)/2，则时间复杂度为O（n²）
平均时间复杂度：O（n²）：平均情况则是n(n-1)/4，也是O（n²）
冒泡排序是稳定的排序算法：
即排序前后，相同元素的顺序不会发生改变
因为冒泡排序只对大小不同的元素进行交换，而相同元素则不会交换位置
冒泡排序是原地排序算法：
原地排序算法指排序的空间复杂度
因为冒泡排序只用了一个额外的temp作为交换的中间值，所以空间复杂度为O（1）；

插入排序

插入排序，将数组分为有序区和无序区，将无序区的元素插入有序区，直至无序区没有元素。
打个比方，就像是打斗地主时，手上抓着一把散乱的扑克牌，我们将扑克牌一张张取出往一端插入，直到手上的扑克牌全都有序为止。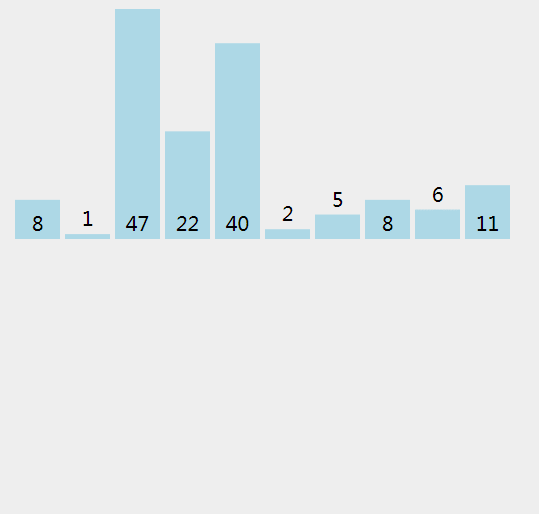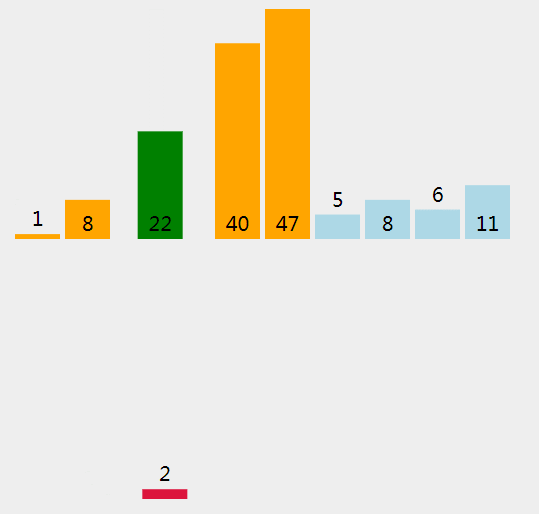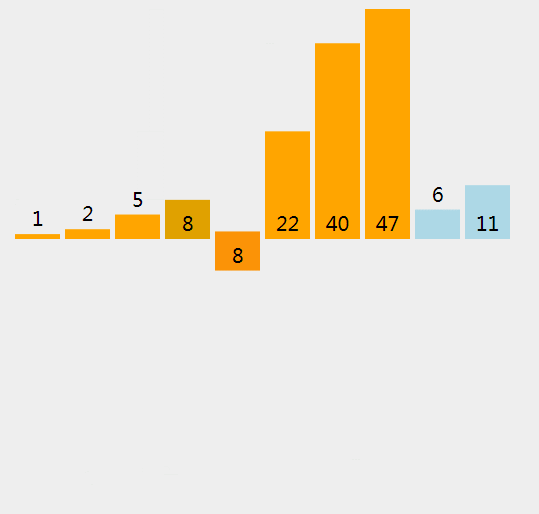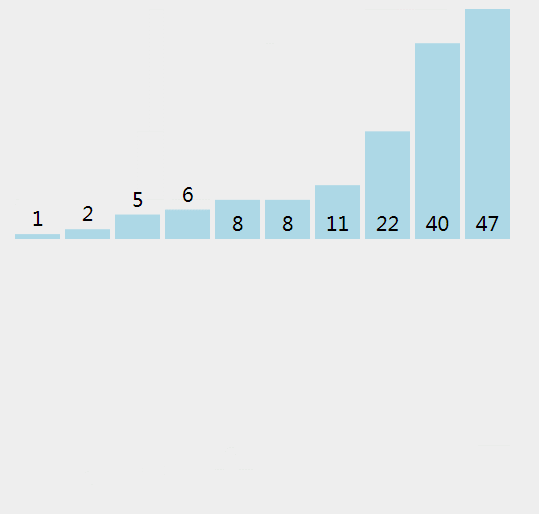

public static void  insertsort(int []a){
    int n =a.length;
    if(n<=1) return;

    for (int i = 1; i < n; i++) {//O（n）
        int value = a[i];//待插入的数据
        int j = i-1;
        for (;j>=0;j--){//查找插入的位置
            if (a[j]>value){//如果该值比待插入数据大，则向右搬移
                a[j+1]=a[j];//数据搬移
            }
            else break;;
        }
        a[j+1]=value;//插入元素
    }
}

插入排序的时间复杂度
最好时间复杂度：O（n）：即数组已经有序，只需要遍历一次，从尾到头在有序区中查找插入位置，内部循环始终是O（1），值得注意的是这是从尾到头遍历
最坏时间复杂度：O（n²）：即数组逆序，则需要n次插入操作，则时间复杂度为O（n²）
平均时间复杂度：O（n²）：每次在数组插入一个数据的时间复杂度为O（n），循环执行n次操作也是O（n²）
插入排序是稳定的排序算法：
因为插入排序中，比待插入的元素大的向后移动，而当元素相同时，则不进行数据搬移，插在相同元素的后面，则没有发生位置变换
插入排序是原地排序算法：
没有使用额外的存储空间，所以是原地排序算法

而相对于冒泡排序，看似时间复杂度差不多，但插入排序的插入操作比冒泡排序的交换操作步骤更少，实际上插入排序的性能要优于冒泡排序

选择排序

选择排序像插入排序一样，分为有序区和无序区，每次从无序区找到最小的元素，放到有序区的末尾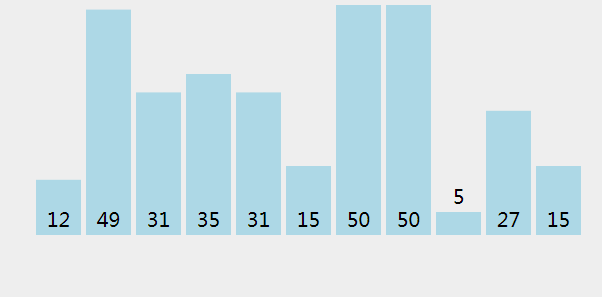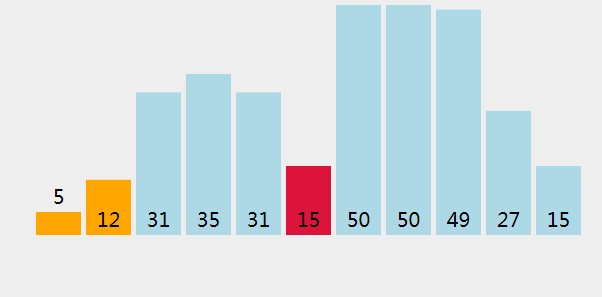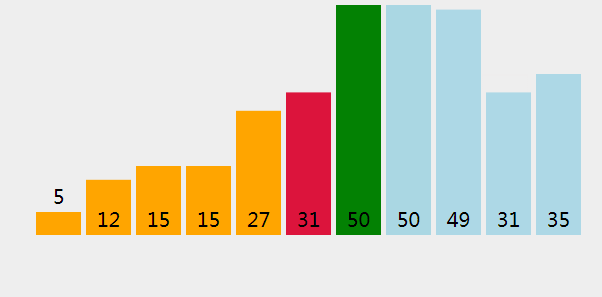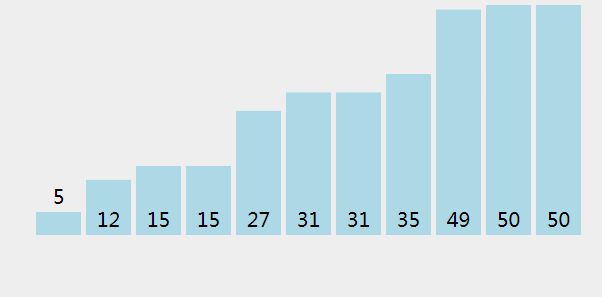

public static void selectionSort(int [] a){
    int n = a.length;
    if (n<=1) return;;
    int temp;
    for (int i=0;i<n;i++){
        int min=a[i];
        int index=i;
        for (int j = i; j <n; j++) {//找到最小元素和索引
            if (min>a[j]){
                min=a[j];
                index=j;
            }
        }
        //交换元素
        temp=a[i];
        a[i]=min;
        a[index]=temp;
    }
}

选择排序的时间复杂度
最好时间复杂度：O（n²）：即使数组是有序的，也会执行n次查找和n次交换操作
最坏时间复杂度：O（n²）：即数组逆序，时间复杂度同样为为O（n²）
平均时间复杂度：O（n²）：综合起来，平均时间复杂度为O（n^2）
选择排序是不稳定的排序算法：
因为在选择排序中，相同元素的相应位置可能发生变化，比如同样的元素，前一个元素发生了交换操作，移动到了另一个相同元素的后方
选择排序是原地排序算法：
和冒泡排序相似，只使用了常量级的额外空间，所以是原地排序算法