声明:文章仅作知识整理、分享,如有侵权请联系作者删除博文,谢谢!
1 背景
1.1 行业背景
尽管模型size在不断地压缩,但是其计算量通常还是有一两百MFLOPS的样子,这个计算量对于目前的移动端CPU算力来说,还是有点吃力的,因此模型端做了最大的努力,我们移动端也要不甘示弱努力加油啊!
通常移动端加速的方案时分CPU派跟GPU派的,目前在低端机型上arm的mali GPU性能惨不忍睹,所以基本配备的还是CPU方案,而中高端机其配备的GPU大部分就是高通的了,其性能还是要比CPU强劲满多的,因此,目前在不同的定位平台上不同的方案各有优势。

上图时前两天(2018.7.12)在腾讯做介绍的ppt,可以看到性能爆炸啊!也就是说arm在cpu这块会针对性地加强AI能力,我们再看个截图:

看红色框内,也就是说arm会在cpu里面加大AI的算力,目前GPU大概就比CPU强个几倍的样子吧!(高端机还不一定有这么多,特别时ARMV8-A64V3系列的点乘出来后)但是这里说的是50倍、80倍啊!简直不敢想象!未来可期!
然后在CPU端做优化,我们可以从上到下考虑:
- 最上面就是算法层,我们可以用winograd从数学上减少乘法的数量(仅在大尺寸下有效),可以用int8量化策略;
- 框架实现层可以实现内存池、多线程等策略;
- 底层就是硬件相关细节了:硬件架构特性、pipeline、cache、内存数据重排、NEON汇编优化等。。。
底层的我之前已讨论过一部分,后面继续补充,这次先讨论量化方法。
1.2 量化三问
1) 为什么量化有用?
因为CNN对噪声不敏感。
2) 为什么用量化?
模型太大,比如alexnet就200MB,贼大,存储压力太大啦;每个层的weights范围基本都是确定的,且波动不大。而且减少访存减少计算量,优势很大的啊!
3) 为什么不直接训练低精度的模型?
因为你训练是需要反向传播和梯度下降的,int8就非常不好做了,举个例子就是我们的学习率一般都是零点几零点几的,你一个int8怎么玩?其次大家的生态就是浮点模型,因此直接转换有效的多啊!
2 量化策略
2.1 量化原理
目前主流用的都是英伟达的tensorRT方案,直接量化,无需retrain,实现简单;
其次就是谷歌的那套方案,稍显复杂需要retrain;
但是我们假如合起来的话,利用英伟达的简单和谷歌的retrain,说不定能达到一个比较高的高度,甚至时顶端!
retrain的要求就是,你的权值、激活值(实测对最终精度的影响不是很大)都必须是分布比较均匀的,也就是方差不要太大。其次是能否控制每层的输出在一定的范围内,这对我们做int8量化时,溢出的处理很有帮助。
NVIDIA的方案是公开了的,但是并没有开源,也就是说你只能用他的那一套工具(tensorRT)来进行量化、部署,当然很正常的,我们也想用他的量化校准部分获取校准参数,然后移动端直接用,目前发现是导不出来这些中间参数的,而且也没源码,在安装包内的python接口也是调用的so文件;
它们给的ppt链接如下:
http://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf
接下来我在这章将详细分析其原理以及python实现,并将在实现过程中碰到的坑一一解剖之(也就是ppt中说的一个很简单的思路,但是在实现的时候是有很多小细节是不确定的,需要一一验证的,NVIDIA的ppt是不会告诉你这些细节的,需要我们来好好理解消化)。
我们首先整体过一遍原理:
我们的目的是把原来的float32bit 的卷积操作(乘加指令)转换为int8的卷积操作,这样计算就变为原来的1/4,但是访存并没有变少,因为我们是在kernel里面才把float32变为int8进行计算的。
最粗糙最本质的原理就是这个图:

很简单是吧!就是把你一个layer的激活值范围的给圈出来,然后按照绝对值最大值作为阀值(因此当正负分布不均匀的时候,是有一部分是空缺的,也就是一部分值域被浪费了;这里有个小坑就是,假如我的激活址全是正的,没有负值,那么你怎么映射呢?),然后把这个范围直接按比例给映射到正负128的范围内来,公式如下:
FP32 Tensor (T) = scale_factor(sf) * 8-bit Tensor(t) + FP32_bias (b)通过实验得知,bias值去掉对精度的影响不是很大,因此我们直接去掉:
T = sf * t上面是简单的max-max 映射,这是针对均匀分布的,很明显的可以知道,只要数据分布的不是很均匀,那么精度损失是很大明显的,于是很多情况下是这么干的:

这个图我们来粗略解读下:
首先要知道为什么量化是可以保证原信息的,这个原因就好比高清图跟低分辨率图的区别,只要你的目标是大体识别出图中是啥这一信息,那么低分辨率的图也是允许的。
你看网上的视频加入马赛克后还会不会影响你的判断呢?并不会,你会脑补出额外的细节,只有当满屏的马赛克的时候才会影响你的观影体验,因此这个打码,噢不,量化其实就是一个程度的问题,一个你能否接受的程度问题。
为什么说最大值映射会精度损失严重?
你看值的分布,由于正负分布很不均匀,如果按照对称最大值映射(原意是为了尽可能多地保留原信息)的话,那么+max那边有一块区域就浪费了,也就是说scale到int8后,int8的动态范围就更小了,举个极限的例子就是量化后原本int8的动态范围只剩1bit了(就是正的样本没有,负的全部扎堆在一个很小的值附近),就是上面说到的满屏马赛克~这种情况下。。。那还表示个毛的原信息啊!
为什么右边的饱和截取就ok呢?
因为非饱和截取的问题是当数据分布极不均匀的时候,有很多动态范围是被浪费的,也就是说打的马赛克很大!而饱和截取就是弥补这个问题的。
当你数据分布很不均匀的时候,如图左边比右边多,那么我把原始信息在影射之前就截断一部分,然后构成对称且分布良好的截断信息,再把这个信息映射到int8上去,那么就不会有动态范围资源被浪费了,也就是说马赛克打的比较细腻了~
像图上这样,先找一个阀值T,然后低于最低阀值的就全部都饱和映射到-127上,如上图的三个红色的点就是这么处理的。
(这也就是一个很自然的思路对吧~把无关的高频细节给去掉,从而获取性能上的好处!网络图像压缩技术不就是这么整的么!PCA主成分、傅立叶分解的思路不都是这样的么!抓住事物的主要矛盾,忽略细节,从而提高整体性能!就像机器学习里的正则化优化不也是这样么,避免你过于钻到细节里面从而产生过拟合啊!这么一想,其实,我们人生不也是这样么?什么事情都得抠死理,钻牛角尖么?!!有时候主动放弃一些东西首先你的人生肯定会轻松很多,其次说不定会收获到更稳定的人生幸福值(泛化性能)呢!)
那么我们的问题就转换为如何寻找最优的阀值T使得精度的损失最小~
损失最小,不就是一个最优化问题嘛~会议下研一时,老师上课说的。。。。
嗯~我忘记了。。。
但是,我们可以凭本能来思考啊!也就是一个正常人会怎么思考!
首先自然地,你会想到用一个模型来描述它吧!那么我们得先建模啊,建立一个模型来评估量化前后的精度损失,然后使得损失最小!
嗯。。。其实所谓的模型就是高数里面的函数嘛!比如椭圆公式就是一个椭圆模型的描述,里面的那些参数就是针对我们特定任务要求的值!
ok~那下一层就是我们如何设计这个模型函数呢?
嗯~其实目前我时肯定想不到怎么去用数学语言描述这个优化问题!毕竟我的数学应用能力还停留在考试中应用题的等级啊!说到底就是数学的功底和悟性不行!
但是,这完全不能阻挡我对数学的向往和追求啊!
当你体验到数学是如何巧妙描述一个复杂事情后你就会体验到她的奇妙~忍不住赞叹,妙啊!
咳~闲话不多说!我们来学习下NVIDIA的思路!
NVIDIA选择的是KL-divergence,其实就是相对熵,那为什么要选择相对熵呢?而不是其他的别的什么呢?因为相对熵表述的就是两个分布的差异程度,
放到我们的情境里面来就是量化前后两个分布的差异程度,差异最小就是最好的了~因此问题转换为求相对熵的最小值!
这里放个公式啊!大学本科水平就能理解的,这里其实就是信息论里面的编码章节问题啊!下面有个链接,我看你骨骼惊奇,是个学习的奇才,传送过去复习下吧!
信息熵,交叉熵和相对熵 - PilgrimHui - 博客园
这个是信息量熵的式子:
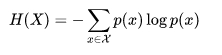
也就是log(1/p)的期望,即事件发生概率的倒数的期望;
熵越大就代表事件发生的概率小,即不可能性大,因此里面包含的信息量就越大.按照真实分布p来编码样本所需的编码长度的期望如下图,这就是上面说的信息熵H( p )。
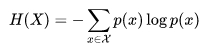
按照不真实分布q来编码样本所需的编码长度的期望如下图,这就是所谓的交叉熵H( p,q )
![]()
这里引申出KL散度D(p||q) = H(p,q) - H(p) =下图公式,也叫做相对熵,它表示两个分布的差异,差异越大,相对熵越大。
![]()
上面公式展开就是这样了:
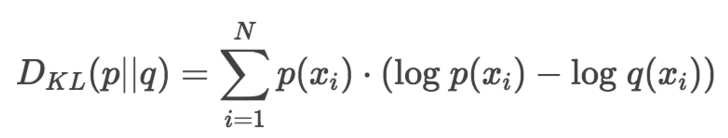
最开始熵就是这么来的啊!然后在编码理论里面,把log的底变为2,出来的就是bit位数了啊!也就是说我来描述一段信息的信息量需要多少个bit(期望值)!
再举个例子?
从编码的角度来讲一下相对熵,即什么是KL-divergence为什么要用KL-divergence?
假设我们有一系列的符号,知道他们出现的概率,如果我要对这些符号进行最优编码,我会用T bits来表示,T即为表示原信息的最优的bit位数。我们把这个编码叫为A;
现在我们有同样的符号集合,只是他们出现的概率变了,假如我还是用A编码来对这个符合集合进行编码的话,那么编码的位长T'就是次优的了,是大于原来的T值的。
(假设我有一系列的符号,我知道它们发生的概率。如果我要对这些符号进行最优的编码,我会用“T”来表示。注意,T是位的最优数。让我们把这段代码称为“A”。现在,我有相同的符号集但是它们发生的概率已经改变了。现在,符号有了新的概率,如果我用代码A来编码符号,编码的比特数将会是次优的,大于T。)
KL散度就是来精确测量这种最优和次优之间的差异(由于选择了错误的编码导致的)。
在这里F32就是原来的最优编码,int8就是次优的编码,我们用KL散度来描述这两种编码之间的差异;
相对熵表示的是采用次优编码时你会多需要多少个bit来编码,也就是与最优编码之间的bit差;
而交叉熵表示的是你用次优编码方式时确切需要多少个bits来表示;
因此,最优编码所需要的bits=交叉熵-相对熵;
我们再写个代码来验证下原理哈:
下面代码的过程就是生成两个随机分布,值在1到11之间,取10个值,然后计算这两个分布之间的KL值,当KL低于0.1时我们看一下它真实的分布,来直观感受下。
def get_KL():
# 随机生成两个离散型分布
x = [np.random.uniform(1, 11) for i in range(10)]
px = x / np.sum(x)
y = [np.random.uniform(1, 11) for i in range(10)]
py = y / np.sum(y)
KL = 0.0
for i in range(10):
KL += px[i] * np.log(px[i] / py[i])
if KL < 0.1:
print x
print y
return KL图形显示就是如下:

上图是其中两组相对熵小于0.1的数据,可见,确实是相似的。好了,现在我假设你已经大概理解了,为什么要用相对熵来描述int8量化后的值分布跟f32的值分布之间的信息量丢失程度!
那公式有了,按照公式的要求,我们接下来就是要求概率了,即事件q(int8)的概率以及事件p(f32)的概率!
额~发现没有!我们遇到坑了!我们的f32值分布是在一个范围内,我们是得分bin才能求bin的概率对吧!那么分多少个bin呢?
NVIDAIA给的是2048个bin,比128bin要多,但是又不会多处太多从而迭代太多影响计算速度!
2.2 量化流程
你看下面是NVIDIA的运算流程:
首先准备一个校准数据集。
然后,对每一层:
- 收集激活值的直方图;
- 基于不同的阀址产生不同的量化分布;
- 然后计算每个分布与原分布的相对熵,然后选择熵最少的一个,也就是跟原分布最像的一个。
此时阀就选出来啦,对应的scale值也就出来了。

calibration:基于实验的迭代搜索阀值。
校准是其核心部分,应用程序提供一个样本数据集(最好是验证集的子集),称为“校准数据集”,它用来做所谓的校准。
在校准数据集上运行FP32推理。收集激活的直方图,并生成一组具有不同阈值的8位表示法,并选择具有最少kl散度的表示; kl-散度是在参考分布(即FP32激活)和量化分布之间(即8位量化激活)之间。
TRT.2.1提供了IInt8EntropyCalibrator,该接口需要由客户端实现,以提供校准数据集和一些用于缓存校准结果的样板代码。
2.3 量化实现
2.3.1 量化流程伪代码

首先看上图的原理,就是把大范围的一个值给缩小到一个小范围的值,注意是等比例的缩小哈~
公式是:FP32 Tensor (T) = scale_factor(sf) * 8-bit Tensor(t),bias实验得知可去掉。
这里看他的意思就是输入为[0, 2048] bins,然后想办法把这么大的值给找到一个合理的阀值T然后映射到int8来。
怎么做的呢?
1.首先不断地截断参考样本P,长度从128开始到2048,为什么从128开始呢?因为截断的长度为128的话,那么我们直接一一对应就好了,完全不用衰减因子了;
2.将截断区外的值全部求和;
3.截断区外的值加到截断样本P的最后一个值之上;(截断区之外的值为什么要加到截断区内最后一个值呢?我个人理解就是有两个原因,其一是求P的概率分布时,需要总的P总值,其二将截断区之外的加到截断P的最后,这样是尽可能地将截断后的信息给加进来。)
4.求得样本P的概率分布;
5.创建样本Q,其元素的值为截断样本P的int8量化值;
6.将Q样本长度拓展到 i ,使得和原样本P具有相同长度;
7.求得Q的概率分布;
8.然后就求P、Q的KL散度值就好啦~
上面就是一个循环,不断地构造P和Q,并计算相对熵,然后找到最小(截断长度为m)的相对熵,此时表示Q能极好地拟合P分布了。
而阀值就等于(m + 0.5)*一个bin的长度;
2.3.2 量化实现代码(python)
上面的流程很清楚吧!我们直接照着实现就好了!我们先看下sensenet的实现:
def threshold_distribution(distribution, target_bin=128):
"""
Returen the best cut off num of bin
Args:
distribution: list, activations has been processed by histogram and normalize,size is 2048
target_bin: int, the num of bin that is used by quantize, Int8 default value is 128
Returns:
target_threshold: int, num of bin with the minimum KL
"""参数中值得关注的是,输入的分布是直方图,2048bins,并且经过了归一化处理。
target_threshold = target_bin
min_kl_divergence = 1000
length = distribution.size
quantize_distribution = np.zeros(target_bin)
threshold_sum = 0.0
threshold_sum = sum(distribution[target_bin:])#这是把128bins之后的累加起来;
for threshold in range(target_bin, length):#不断地在128~2048之间移动阀址T;
t_distribution = copy.deepcopy(distribution[:threshold])
t_distribution[threshold - 1] = t_distribution[threshold - 1] + threshold_sum
threshold_sum = threshold_sum - distribution[threshold]这里我认为是有问题的,首先我们来看下原伪代码:

你看它上面的python实现,先把128~2048bins的值求和,然后在每次的迭代阀址过程中给加到截断分布的最后位置上;
伪代码不好的地方在于每次都要计算截断区之外的值之和,这样很费时间,因此上面代码的实现方式就是先求一个最长的和,然后依次减去前面那一个就好了,这样性能会提升的。
# ************************ threshold ************************
插值处理部分:
quantize_distribution = np.zeros(128)
num_per_bin = threshold / target_bin #阀址区域跟量化区域的比值,用来确定几个bins要挤进一个bin之内。
for i in range(0, 128):
start = i * num_per_bin
end = start + num_per_bin # (i+1)*num_per_bin
left_upper = (int)(math.ceil(start)) #向上取整
if (left_upper > start): #就是说现在取的截断区域不是在128的整数倍区域处。
left_scale = left_upper - start # ceil(start) - start
quantize_distribution[i] += left_scale * distribution[left_upper - 1]
right_lower = (int)(math.floor(end)) #向下取整
if (right_lower < end):
right_scale = end - right_lower
quantize_distribution[i] += right_scale * distribution[right_lower]
for j in range(left_upper, right_lower):
quantize_distribution[i] += distribution[j]
# ************************ threshold ************************
# ************************ quantzie ************************
expand_distribution = np.zeros(threshold, dtype=np.float32)
for i in range(0, target_bin):
start = i * num_per_bin
end = start + num_per_bin
count = 0
left_upper = (int)(math.ceil(start))
left_scale = 0.0
if (left_upper > start):
left_scale = left_upper - start
if (distribution[left_upper - 1] != 0):
count += left_scale
right_lower = (int)(math.floor(end))
right_scale = 0.0
if (right_lower < end):
right_scale = end - right_lower
if (distribution[right_lower] != 0):
count += right_scale
for j in range(left_upper, right_lower):
if (distribution[j] != 0):
count = count + 1
expand_value = quantize_distribution[i] / count
if (left_upper > start):
if (distribution[left_upper - 1] != 0):
expand_distribution[left_upper - 1] += expand_value * left_scale
if (right_lower < end):
if (distribution[right_lower] != 0):
expand_distribution[right_lower] += expand_value * right_scale
for j in range(left_upper, right_lower):
if (distribution[j] != 0):
expand_distribution[j] += expand_value
# ************************ quantzie ************************
kl_divergence = compute_kl_divergence(t_distribution, expand_distribution)
if kl_divergence < min_kl_divergence:
min_kl_divergence = kl_divergence
target_threshold = threshold
return target_threshold可以看到权值的量化贼方便,就是找到最大最小值,然后选择其中绝对值最大的值,然后以此等比例量化,得到weight_scale;
def weight_quantize(net, net_file):
# find the convolution 3x3 and 1x1 layers to get out the weight_scale
if (layer.type == "Convolution" or layer.type == "ConvolutionDepthwise"):
if (kernel_size == 3 or kernel_size == 1):
# find the blob threshold
max_val = np.max(weight_data)
min_val = np.min(weight_data)
threshold = max(abs(max_val), abs(min_val))
weight_scale = 127 / threshold然后,你发现没?其实这个是有点瑕疵的,比如我的权值分布是很不均匀的,全都在正的值,大值区域内那么一小撮,那么这样子的话量化完之后,正负128的范围也只有128附近才有值的啊!