四、VAR 模型
向量自回归介绍：
当我们对变量是否真是外生变量的情况不自信时，传递函数分析的自然扩展就是均等地对待每一个变量。在双变量情况下，我们可以令{yt}的时间路径受序列{zt}的当期或过去的实际值的影响，考虑如下简单的双变量体系
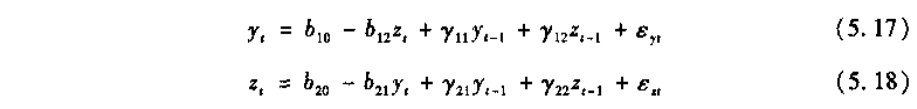
式(5.17)和(5.18)并非是诱导型方程，因为yt对zt有一个同时期的影响，而zt对yt也有一个同时期的影响。所幸的是，可将方程转化为更实用的形式，使用矩阵性代数，我们可将系统写成紧凑形式：
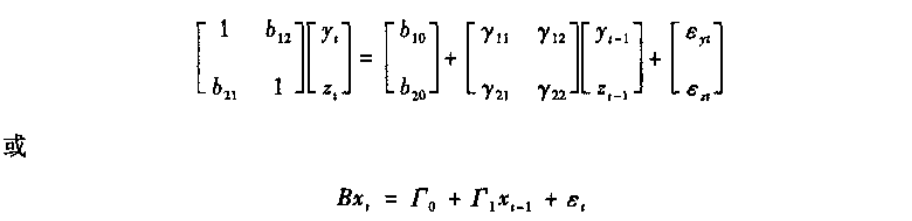
其中
也等价于：
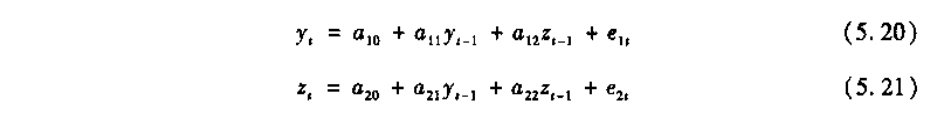
在实际的应用估计中，我们并不能够直接估计出结构性VAR方程，因为在VAR过程中所固有的反馈，直接进行估计的话，则zt与误差项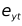
相关，yt与误差项
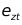相关，但是标准估计要求回归变量与误差项不相关。
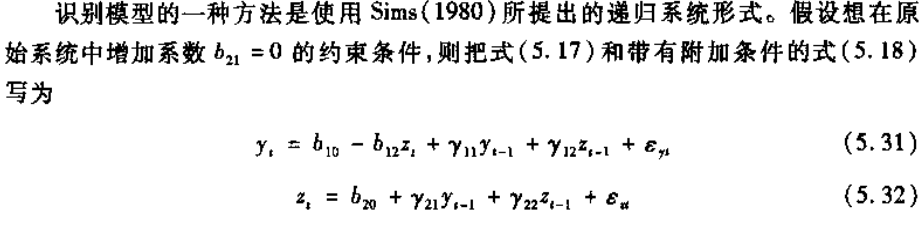
因为在识别结构VAR方程时，需要对估计变量进行约束，这样子也就造成了在进行标准VAR估计后，求正交化的脉冲响应函数时，进行估计的变量排列序列会造成脉冲响应函数有些区别。因为在求正交化的脉冲响应函数时，是要得到变量的独立冲击，是要求出各自的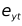和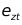以及其滞后n项。
脉冲响应函数用于衡量来自随机扰动项的冲击对内生变量当前和未来值的影响。
方差分解是将系统的预测均方误差分解成为系统中各变量冲击所做的贡献，把系统中任意一个内生变量的波动按其成因分解为与各方程新息相关联的若干个组成部分，从而了解各新息对模型内生变量的相对重要性，即变量的贡献占总贡献的比例。
Granger非因果性检验：
(1)滞后期 k 的选取以 VAR 为依据。实际中是一个判断性问题。以 xt和 yt为例，如果xt-1对 yt存在显著性影响，则不必再做滞后期更长的检验。如果 xt-1对 yt不存在显著性影响，则应该再做滞后期更长的检验。一般来说要试检验若干个不同滞后期 k的格兰杰因果关系检验，且结论相同时，才可以最终下结论。
(2)格兰杰非因果性。
(3)通常总是把 xt-1 对 yt存在非因果关系表述为 xt(去掉下标-1)对 yt存在非因果关系(严格讲，这种表述是不正确的)。
(4)Granger非因果性检验只在平稳变量之间进行。不存在协整关系的非平稳变量之间不能进行格兰杰因果关系检验。
(5)格兰杰因果关系不是哲学概念上的因果关系。一则他表示的是 xt-1对 yt的影响。二则它只是说明 xt可以作为yt变化的预测因子。
VAR 模型的特点是：
(1)不以严格的经济理论为依据。在建模过程中只需明确两件事：①共有哪些变量是相互有关系的，把有关系的变量包括在 VAR 模型中；②确定滞后期 k。使模型能反映出变量间相互影响的绝大部分。
(2)VAR 模型对参数不施加零约束。(对无显着性的参数估计值并不从模型中剔除，不分析回归参数的经济意义。)
(3)VAR模型的解释变量中不包括任何当期变量，所有与联立方程模型有关的问题在VAR 模型中都不存在(主要是参数估计量的非一致性问题)。
(4)VAR 模型的另一个特点是有相当多的参数需要估计。比如一个 VAR 模型含有三个变量，最大滞后期 k = 3，则有 kN^2= 3×3^2= 27个参数需要估计。当样本容量较小时，多数参数的估计量误差较大。
(5)无约束 VAR 模型的应用之一是预测。由于在 VAR 模型中每个方程的右侧都不含有当期变量，这种模型用于样本外一期预测的优点是不必对解释变量在预测期内的取值做任何预测。
(6)用VAR模型做样本外近期预测非常准确。做样本外长期预测时，则只能预测出变动的趋势，而对短期波动预测不理想。
(7)VAR模型中每一个变量都必须具有平稳性。如果是非平稳的，则必须具有协整关系。
西姆斯(Sims)认为VAR模型中的全部变量都是内生变量。近年来也有学者认为具有单向因果关系的变量，也可以作为外生变量加入VAR 模型。
4.1 滞后阶数的选择
在VAR模型中，正确选择模型的滞后阶数对于模型估计和协整检验都产生一定的影响，在小样本中情况更是如此。Stata中varsoc命令给出了滞后阶数选择的几种标准，包括最终预测误差(Final Prediction Error,FPE)、施瓦茨信息准则(Schwarz's Bayesian Information Criterion,SBIC)、汉南—昆(Hannan and Quinn Information Criterion,HQIC)。对于这些检验，相对于默认的算法，还有另一种算法是lutstats，其运行出来的结果有差别，但对于判断没有多大的影响。
例子：
. use http://www.stata-press.com/data/r11/lutkepohl2,clear
(Quarterly SA West German macro data, Bil DM, from Lutkepohl 1993 Table E.1)
. varsoc dln_inv dln_inc dln_consump if qtr<=tq(1978q4),lutstats< span="">
Selection-order criteria (lutstats)
Sample: 1961q2 - 1978q4 Number of obs = 71
+---------------------------------------------------------------------------+
|lag | LL LR df p FPE AIC HQIC SBIC |
|----+----------------------------------------------------------------------|
| 0 | 564.784 2.7e-11 -24.423 -24.423* -24.423* |
| 1 | 576.409 23.249 9 0.006 2.5e-11 -24.497 -24.3829 -24.2102 |
| 2 | 588.859 24.901* 9 0.003 2.3e-11* -24.5942* -24.3661 -24.0205 |
| 3 | 591.237 4.7566 9 0.855 2.7e-11 -24.4076 -24.0655 -23.5472 |
| 4 | 598.457 14.438 9 0.108 2.9e-11 -24.3575 -23.9012 -23.2102 |
+---------------------------------------------------------------------------+
Endogenous: dln_inv dln_inc dln_consump
Exogenous: _cons
对于给定的一个p阶，LR检验将比较p阶的VAR和p-1阶的VAR。其检验的虚无假设是内生变量的第p阶系数为零。通过这一连串的LR检验来筛选阶数，我们一般从模型的最大阶数检验的结果开始，也即是表格的底部。第一个拒绝虚无假设的检验的阶数就是这个过程所选择的阶数。
对于其余的统计检验，最小阶数的确定是根据一定的判断准则来选择的，带“*”表示最适阶数。严格来讲，FPE不是一个信息判断准则，尽管我们把它加到判断中来，这是因为根据信息判断准则，我们选择的滞后长度要对应最小的值；自然，我们也想要最小化它的预测误差。AIC准则是测量设定模型和实际模型的差异，这也是我们要尽可能小的。SBIC和HQIC准则的解释与AIC很相似，但SBIC和HQIC比AIC和FPE有理论上的优势。在实际判断中，我们要根据上述的这些检验结果，尽可能的选择满足较多的检验的滞后阶数。
4.2 模型的估计
VAR模型在stata里的命令为var。其中默认的是2阶滞后。
命令格式：var depvarlist [if] [in] [,options]
options包括：
noconstant 没有常数项
lags(numlist) 滞后阶数
exog(varlist) 外生变量
dfk 自由度调整
small 小样本t、F统计量
lutstats Lutkepohl滞后阶数选择统计量
例子1：
. use http://www.stata-press.com/data/r11/lutkepohl2,clear
(Quarterly SA West German macro data, Bil DM, from Lutkepohl 1993 Table E.1)
. var dln_inv dln_inc dln_consump if qtr<=tq(1978q4),lutstats dfk
Vector autoregression
Sample: 1960q4 - 1978q4 No. of obs = 73
Log likelihood = 606.307 (lutstats) AIC = -24.63163
FPE = 2.18e-11 HQIC = -24.40656
Det(Sigma_ml) = 1.23e-11 SBIC = -24.06686
Equation Parms RMSE R-sq chi2 P>chi2
----------------------------------------------------------------
dln_inv 7 .046148 0.1286 9.736909 0.1362
dln_inc 7 .011719 0.1142 8.508289 0.2032
dln_consump 7 .009445 0.2513 22.15096 0.0011
----------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
dln_inv |
dln_inv |
L1. | -.3196318 .1254564 -2.55 0.011 -.5655218 -.0737419
L2. | -.1605508 .1249066 -1.29 0.199 -.4053633 .0842616
|
dln_inc |
L1. | .1459851 .5456664 0.27 0.789 -.9235013 1.215472
L2. | .1146009 .5345709 0.21 0.830 -.9331388 1.162341
|
dln_consump |
L1. | .9612288 .6643086 1.45 0.148 -.3407922 2.26325
L2. | .9344001 .6650949 1.40 0.160 -.369162 2.237962
|
_cons | -.0167221 .0172264 -0.97 0.332 -.0504852 .0170409
-------------+----------------------------------------------------------------
dln_inc |
dln_inv |
L1. | .0439309 .0318592 1.38 0.168 -.018512 .1063739
L2. | .0500302 .0317196 1.58 0.115 -.0121391 .1121995
|
dln_inc |
L1. | -.1527311 .1385702 -1.10 0.270 -.4243237 .1188615
L2. | .0191634 .1357525 0.14 0.888 -.2469067 .2852334
|
dln_consump |
L1. | .2884992 .168699 1.71 0.087 -.0421448 .6191431
L2. | -.0102 .1688987 -0.06 0.952 -.3412354 .3208353
|
_cons | .0157672 .0043746 3.60 0.000 .0071932 .0243412
-------------+----------------------------------------------------------------
dln_consump |
dln_inv |
L1. | -.002423 .0256763 -0.09 0.925 -.0527476 .0479016
L2. | .0338806 .0255638 1.33 0.185 -.0162235 .0839847
|
dln_inc |
L1. | .2248134 .1116778 2.01 0.044 .005929 .4436978
L2. | .3549135 .1094069 3.24 0.001 .1404798 .5693471
|
dln_consump |
L1. | -.2639695 .1359595 -1.94 0.052 -.5304451 .0025062
L2. | -.0222264 .1361204 -0.16 0.870 -.2890175 .2445646
|
_cons | .0129258 .0035256 3.67 0.000 .0060157 .0198358
------------------------------------------------------------------------------
例子2：(包含外生变量的VAR模型)
. use http://www.stata-press.com/data/r11/lutkepohl2,clear
(Quarterly SA West German macro data, Bil DM, from Lutkepohl 1993 Table E.1)
. var dln_inv dln_inc , exog(dln_consump) lag(1/2) small
Vector autoregression
Sample: 1960q4 - 1982q4 No. of obs = 89
Log likelihood = 443.8226 AIC = -9.70388
FPE = 2.09e-07 HQIC = -9.568631
Det(Sigma_ml) = 1.60e-07 SBIC = -9.368333
Equation Parms RMSE R-sq F P > F
----------------------------------------------------------------
dln_inv 6 .042777 0.1553 3.271408 0.0096
dln_inc 6 .010022 0.3152 8.194719 0.0000
----------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
dln_inv |
dln_inv |
L1. | -.2105219 .1014099 -2.08 0.041 -.4122222 -.0088217
L2. | -.1769163 .1041204 -1.70 0.093 -.3840076 .0301749
|
dln_inc |
L1. | .5344701 .3849959 1.39 0.169 -.2312712 1.300211
L2. | .1769331 .3982704 0.44 0.658 -.6152107 .9690769
|
dln_consump | 1.207425 .4456638 2.71 0.008 .3210171 2.093832
_cons | -.0128275 .0115282 -1.11 0.269 -.0357567 .0101017
-------------+----------------------------------------------------------------
dln_inc |
dln_inv |
L1. | .0674255 .0237579 2.84 0.006 .0201719 .1146791
L2. | .0286516 .0243929 1.17 0.244 -.019865 .0771681
|
dln_inc |
L1. | -.0589614 .0901954 -0.65 0.515 -.2383564 .1204336
L2. | -.0702845 .0933053 -0.75 0.453 -.2558649 .115296
|
dln_consump | .5487083 .1044084 5.26 0.000 .3410441 .7563725
_cons | .0097651 .0027008 3.62 0.001 .0043934 .0151369
------------------------------------------------------------------------------
例子3：(正交脉冲响应图形)
. use http://www.stata-press.com/data/r11/lutkepohl2,clear
(Quarterly SA West German macro data, Bil DM, from Lutkepohl 1993 Table E.1)
. varbasic dln_inv dln_inc dln_consump if qtr<=tq(1978q4)< span="">
Vector autoregression
Sample: 1960q4 - 1978q4 No. of obs = 73
Log likelihood = 606.307 AIC = -16.03581
FPE = 2.18e-11 HQIC = -15.77323
Det(Sigma_ml) = 1.23e-11 SBIC = -15.37691
Equation Parms RMSE R-sq chi2 P>chi2
----------------------------------------------------------------
dln_inv 7 .046148 0.1286 10.76961 0.0958
dln_inc 7 .011719 0.1142 9.410683 0.1518
dln_consump 7 .009445 0.2513 24.50031 0.0004
----------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
dln_inv |
dln_inv |
L1. | -.3196318 .1192898 -2.68 0.007 -.5534355 -.0858282
L2. | -.1605508 .118767 -1.35 0.176 -.39333 .0722283
|
dln_inc |
L1. | .1459851 .5188451 0.28 0.778 -.8709326 1.162903
L2. | .1146009 .508295 0.23 0.822 -.881639 1.110841
|
dln_consump |
L1. | .9612288 .6316557 1.52 0.128 -.2767936 2.199251
L2. | .9344001 .6324034 1.48 0.140 -.3050877 2.173888
|
_cons | -.0167221 .0163796 -1.02 0.307 -.0488257 .0153814
-------------+----------------------------------------------------------------
dln_inc |
dln_inv |
L1. | .0439309 .0302933 1.45 0.147 -.0154427 .1033046
L2. | .0500302 .0301605 1.66 0.097 -.0090833 .1091437
|
dln_inc |
L1. | -.1527311 .131759 -1.16 0.246 -.4109741 .1055118
L2. | .0191634 .1290799 0.15 0.882 -.2338285 .2721552
|
dln_consump |
L1. | .2884992 .1604069 1.80 0.072 -.0258926 .6028909
L2. | -.0102 .1605968 -0.06 0.949 -.3249639 .3045639
|
_cons | .0157672 .0041596 3.79 0.000 .0076146 .0239198
-------------+----------------------------------------------------------------
dln_consump |
dln_inv |
L1. | -.002423 .0244142 -0.10 0.921 -.050274 .045428
L2. | .0338806 .0243072 1.39 0.163 -.0137607 .0815219
|
dln_inc |
L1. | .2248134 .1061884 2.12 0.034 .0166879 .4329389
L2. | .3549135 .1040292 3.41 0.001 .1510199 .558807
|
dln_consump |
L1. | -.2639695 .1292766 -2.04 0.041 -.517347 -.010592
L2. | -.0222264 .1294296 -0.17 0.864 -.2759039 .231451
|
_cons | .0129258 .0033523 3.86 0.000 .0063554 .0194962
------------------------------------------------------------------------------
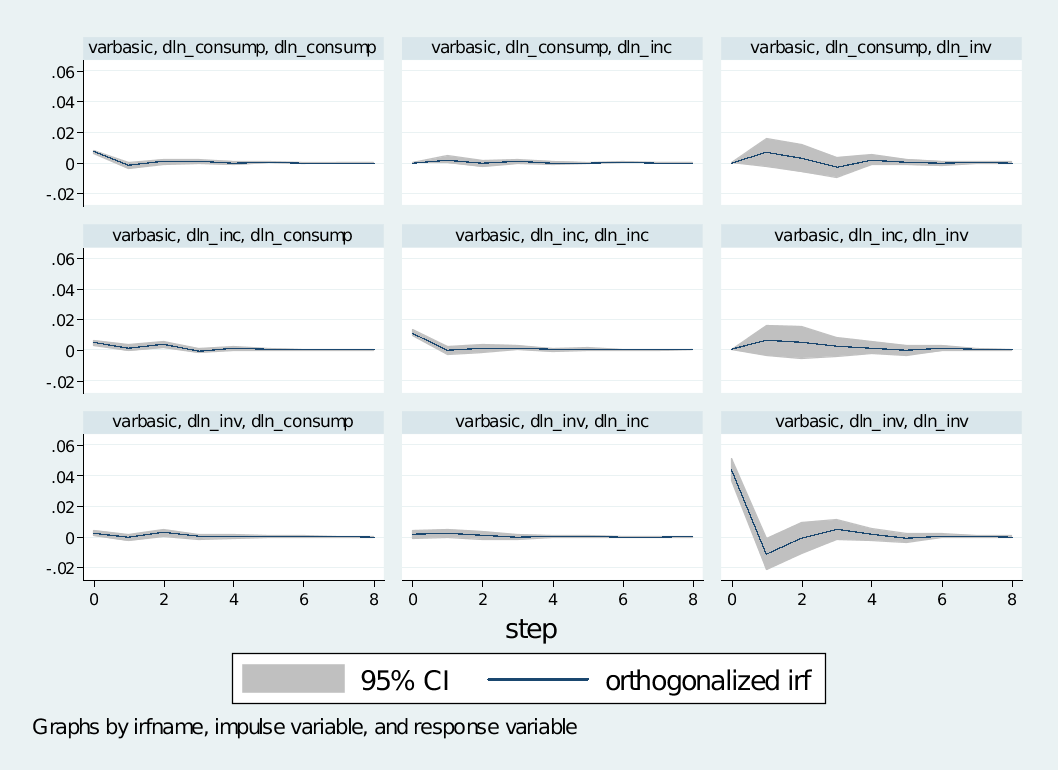
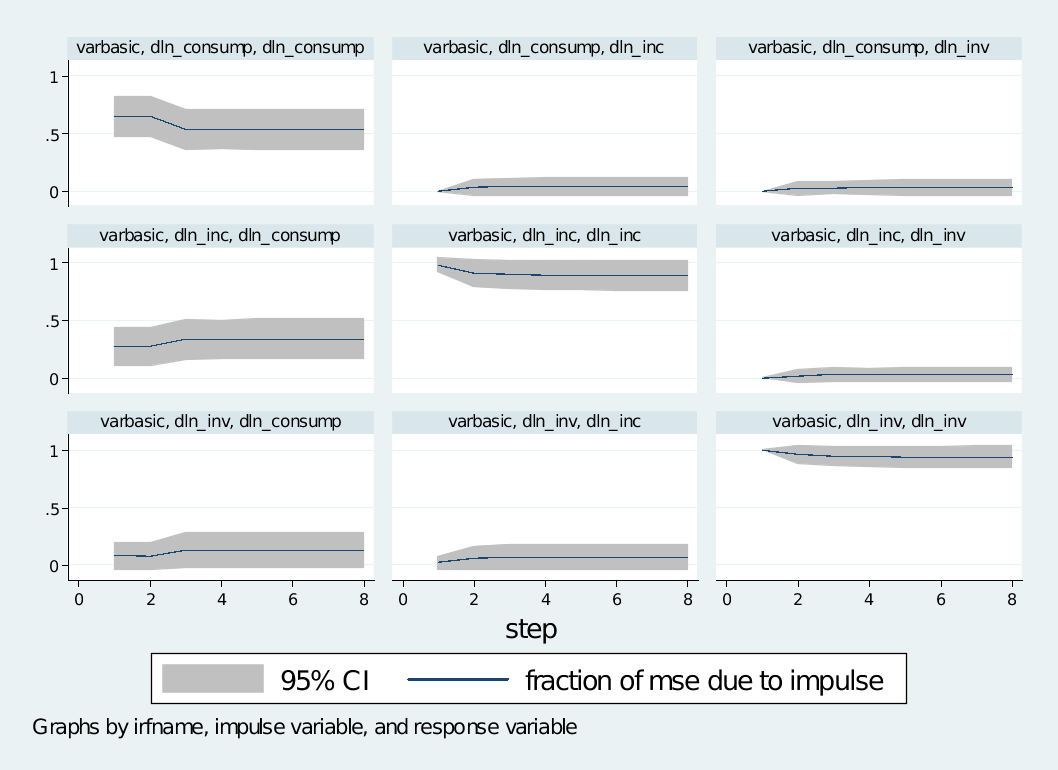
. irf graph fevd,lstep(1)
例子4：脉冲响应图形(未正交化)
. use http://www.stata-press.com/data/r11/lutkepohl2,clear
(Quarterly SA West German macro data, Bil DM, from Lutkepohl 1993 Table E.1)
. varbasic dln_inv dln_inc dln_consump , irf
运行结果省略
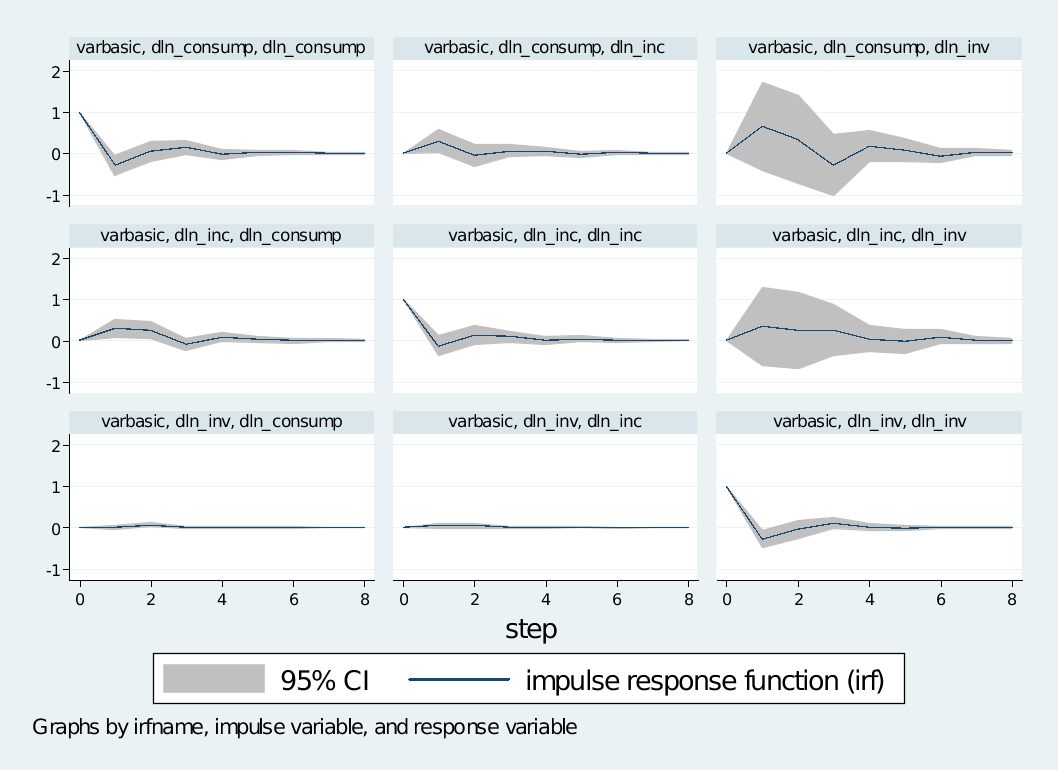
. irf graph irf, lstep(1)
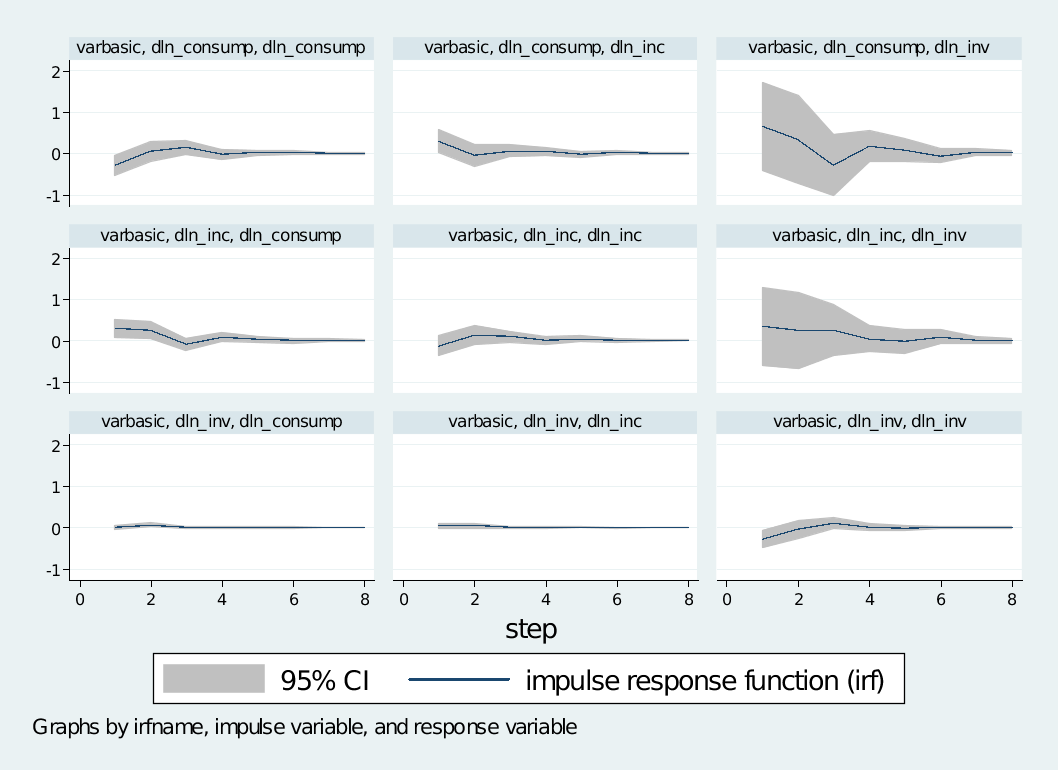
4.3 VAR模型相关检验
1)平稳性检验：命令为varstable
例子：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dln_inv dln_inc dln_consump if qtr>=tq(1961q2) & qtr<=tq(1978q4)< span="">
varstable, graph /*图示模的分布*/
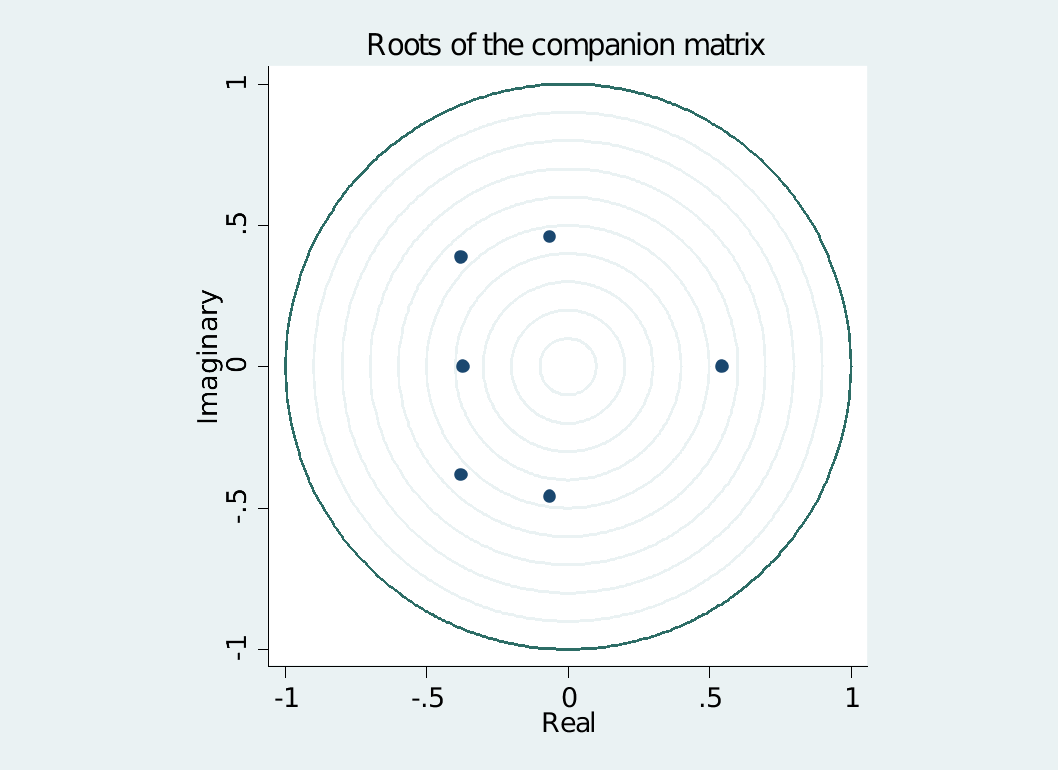
2)检验滞后阶数的显著性：命令varwle
例子：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dln_inv dln_inc dln_consump ,lag(1/2) dfk small
varwle /*检验特定滞后阶数的联合显著性*/
* 处理方法：附加约束条件
constraint define 1 [dln_inv]L2.dln_inv = 0
constraint define 2 [dln_inv]L2.dln_inc = 0
constraint define 3 [dln_inv]L2.dln_consump = 0
constraint define 4 [dln_inc]L2.dln_inv = 0
constraint define 5 [dln_inc]L2.dln_inc = 0
constraint define 6 [dln_inc]L2.dln_consump = 0
var dln_inv dln_inc dln_consump ,lag(1/2) dfk small constraints(1/6)
varwle
3)残差正态分布检验
在stata里，常用的命令为varnorm。它提供了三种检验：峰度、偏度以及Jarque–Bera检验，其中Jarque–Bera检验综合了峰度和偏度的检验，相当于整体的正态分布检验。
例子：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dln_inv dln_inc dln_consump if qtr<=q(1978q4),lag(1/2) dfk small
varnorm
* 三个统计量均无法拒绝残差服从正态分布的原假设
var dln_inv dln_inc dln_consump,lag(1/2) dfk small
varnorm
* 此时可能需要考虑增加滞后阶数或近一步修正模型的设定
4)残差序列相关检验：命令varlmar
当Prob > chi2值大于0.05时，我们就可以判定其不存在自相关。
例子：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dln_inv dln_inc dln_consump if qtr<=q(1978q4),lag(1/2) dfk small
varlmar
varlmar, mlag(5)
4.4 格兰杰因果检验
格兰杰因果检验的命令为vargranger。格兰杰因果检验的虚无假设是X对Y不存在因果关系。在stata的检验结果里面，当P值小于0.05即拒绝虚无假设，即表明X对Y存在因果关系。
例子：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dln_inv dln_inc dln_consump,lag(1/2) dfk small
vargranger
格兰杰因果检验结果如下：
Granger causality Wald tests
+------------------------------------------------------------------------+
| Equation Excluded | F df df_r Prob > F |
|--------------------------------------+---------------------------------|
| dln_inv dln_inc | .25645 2 82 0.7744 |
| dln_inv dln_consump | .89569 2 82 0.4123 |
| dln_inv ALL | 1.6857 4 82 0.1612 |
|--------------------------------------+---------------------------------|
| dln_inc dln_inv | 2.8776 2 82 0.0620 |
| dln_inc dln_consump | 2.3508 2 82 0.1017 |
| dln_inc ALL | 3.0145 4 82 0.0226 |
|--------------------------------------+---------------------------------|
| dln_consump dln_inv | 1.9554 2 82 0.1481 |
| dln_consump dln_inc | 7.4974 2 82 0.0010 |
| dln_consump ALL | 5.0021 4 82 0.0012 |
+------------------------------------------------------------------------+
从上面检验结果我们可以看到，收入的增长对消费增长存在显著影响，以及收入对投资对存在不那么显著的影响。
4.5 脉冲响应和方差分解
脉冲响应和方差分解是一个问题的两个方面。脉冲响应是衡量模型中的内生变量如何对一个变量的脉冲(冲击)做出响应，而方差分解则是如何将一个变量的响应分解到模型中的内生变量。Stata的irf命令用于计算VAR、SVAR、VEC模型的脉冲响应、动态乘子和方差分解。
例子：
* -- 基本步骤
* 步骤1: 估计VAR模型
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dln_inv dln_inc dln_consump,lag(1/2) dfk small
* 步骤2: 生成IRF文件
irf create order1, step(10) set(myirf1) replace
* 步骤3: 画图
irf graph oirf, impulse(dln_inc) response(dln_consump) irf(order1) xlabel(#10)
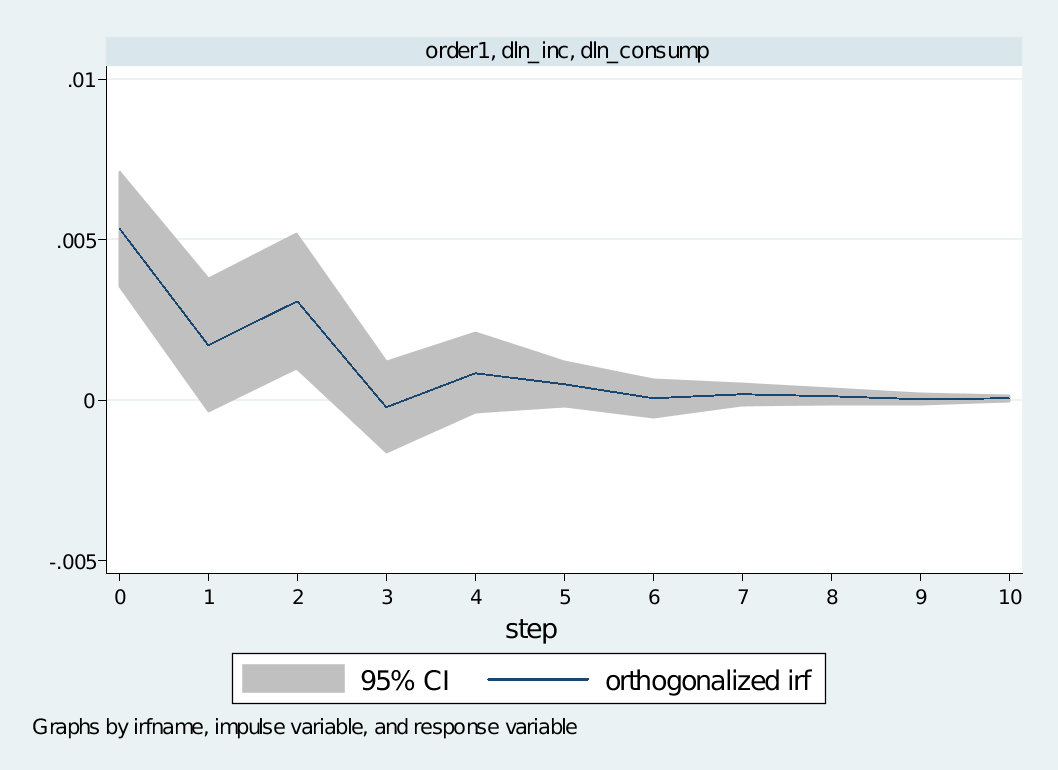
脉冲响应IRF和方差分解FEVD可以产生在同一个文件里头。irf命令产生了myirf1.irf文件和把一种结果模式放在里面，命名为order1。order1结果包括简单脉冲响应、正交化脉冲响应、累积脉冲响应、累积正交化脉冲响应和Cholesky方差分解。
下面我们使用相同的var估计模型，但用另一种不同的命令来产生第二种IRF结果模式，命名为order2储存在相同的文件里面，并画出这两种结果：
irf create order2, step(10) order(dln_inv dln_inc dln_consump) replace
irf graph oirf, irf(order1 order2) impulse(dln_inc) response(dln_consump)
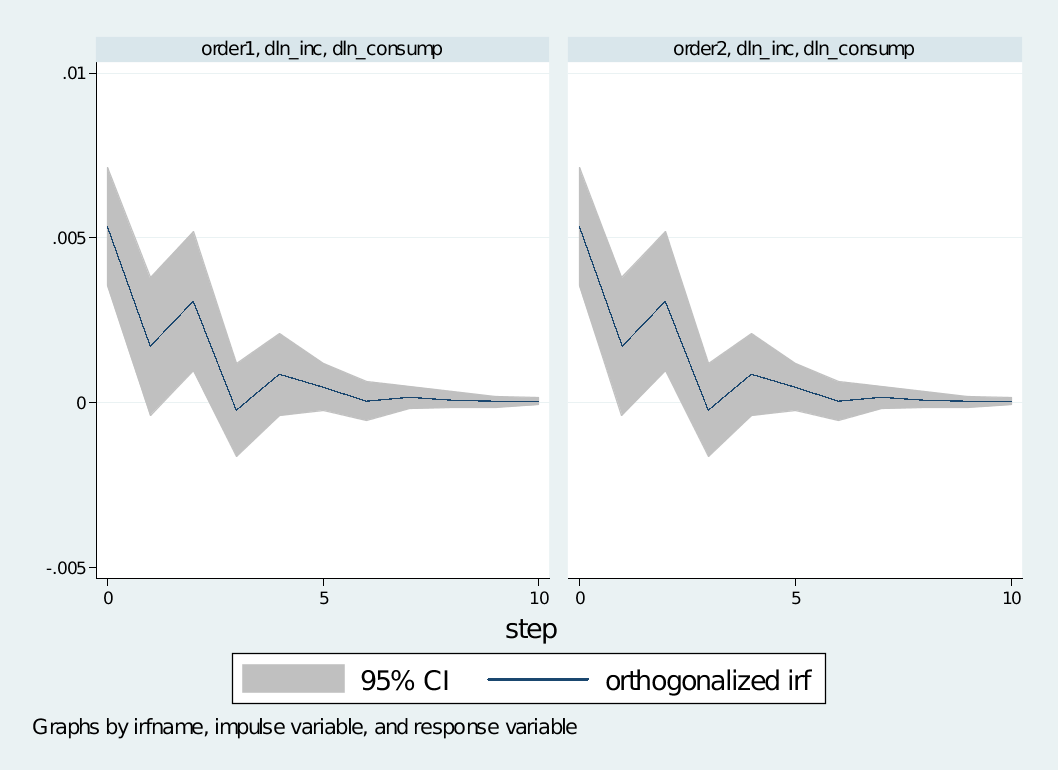
接下来我们用irf table命令用列表式将两种脉冲响应结果表示出来：
irf table oirf, irf(order1 order2) impulse(dln_inc) response(dln_consump)
Results from order1 order2
+--------------------------------------------------------------------------------+
| | (1) (1) (1) | (2) (2) (2) |
| step | oirf Lower Upper | oirf Lower Upper |
|--------+-----------------------------------+-----------------------------------|
|0 | .005338 .003545 .00713 | .005338 .003545 .00713 |
|1 | .001704 -.000385 .003792 | .001704 -.000385 .003792 |
|2 | .003071 .000963 .005179 | .003071 .000963 .005179 |
|3 | -.00023 -.001636 .001176 | -.00023 -.001636 .001176 |
|4 | .000845 -.000402 .002092 | .000845 -.000402 .002092 |
|5 | .000481 -.000227 .001189 | .000481 -.000227 .001189 |
|6 | .000045 -.000539 .00063 | .000045 -.000539 .00063 |
|7 | .000157 -.000187 .000502 | .000157 -.000187 .000502 |
|8 | .000095 -.000148 .000338 | .000095 -.000148 .000338 |
|9 | .000019 -.000142 .00018 | .000019 -.000142 .00018 |
|10 | .000036 -.000065 .000136 | .000036 -.000065 .000136 |
+--------------------------------------------------------------------------------+
95% lower and upper bounds reported
(1) irfname = order1, impulse = dln_inc, and response = dln_consump
(2) irfname = order2, impulse = dln_inc, and response = dln_consump
从图形和表格我们可以得到这两种产生脉冲响应的命令本质上是相同的。在这次脉冲响应过程中，给dln_inc一个增加的正交冲击将引起对dln_consump的一个短暂的持续增加直到第四五期。
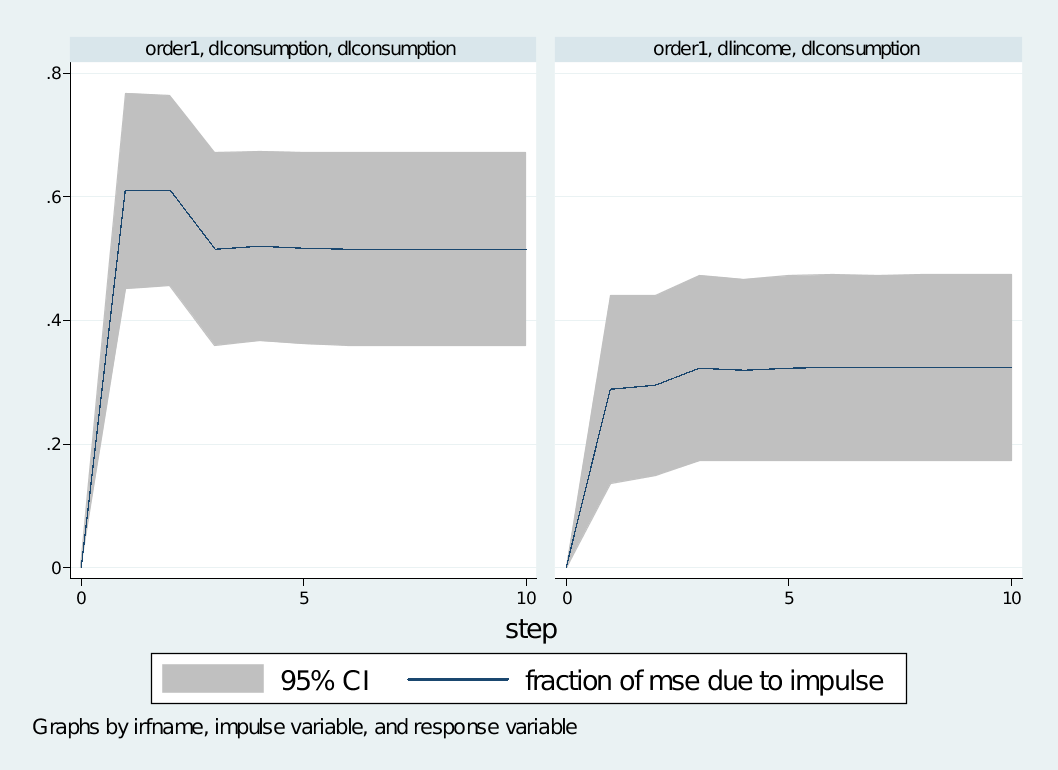
接下来我们也可以来考察收入与消费的方差分解：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dlinvest dlincome dlconsumption,lag(1/2) dfk small
irf create order1, step(10) set(myirf1)
irf graph fevd, irf(order1) impulse(dlincome dlconsumption) response(dlconsumption)
irf graph fevd, irf(order1) impulse(dlincome dlconsumption) response(dlincome)
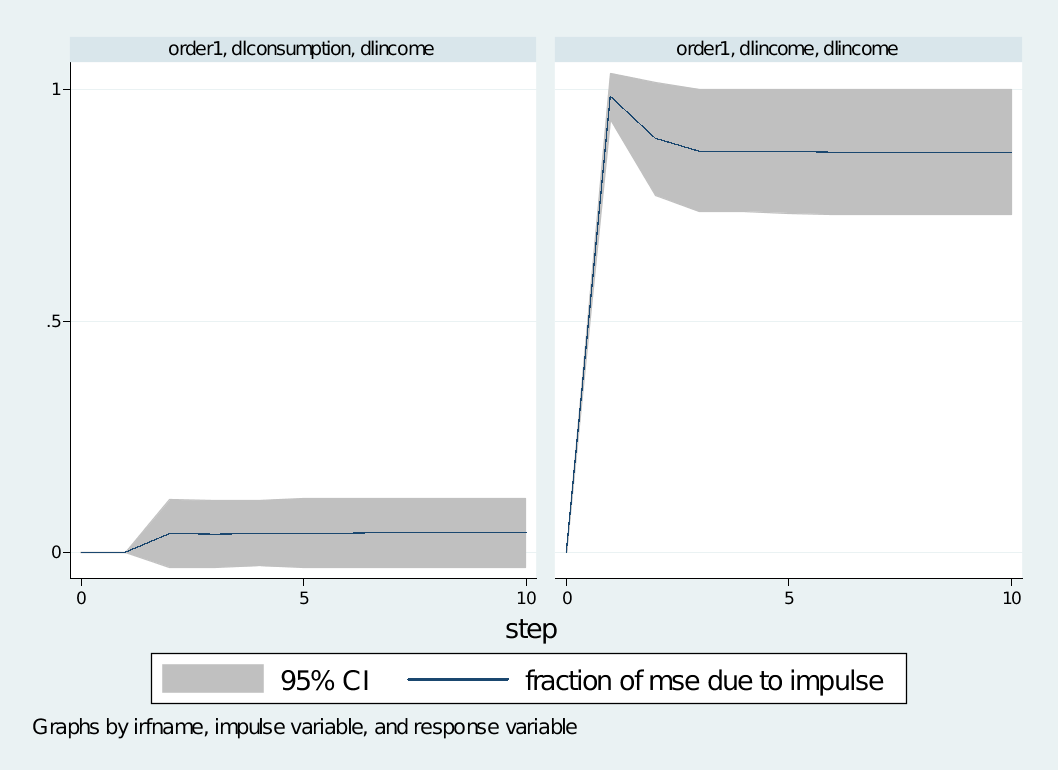
对于 irf graph stat这画图命令，以及irf table stat列表式命令，其中stat的选项有如下几种：
Stat | 类型 | VAR | SVAR | VEC |
oirf | 正交IRF | ˇ | ˇ | ˇ |
dm | 动态乘子 | ˇ | ||
cirf | 累积IRF | ˇ | ˇ | ˇ |
coirf | 累积正交IRF | ˇ | ˇ | ˇ |
cdm | 累积动态乘子 | ˇ | ||
sirf | 结构IRF | ˇ | ||
fevd | Cholesky方差分解 | ˇ | ˇ | ˇ |
sfevd | 结构Cholisky方差分解 | ˇ |
4.6 预测
例子：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
varfcast compute
list dlinvestment dlinvestment_f dlinvestment_f_L ///
dlinvestment_f_U dlinvestment_f_se in 91/93
*-- 样本内一步预测: dynamic()选项
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dlinvest dlincome dlconsumption,lag(1/2) dfk small
varfcast compute, dynamic(5)
list dlinvestment dlinvestment_f dlincome dlincome_f ///
dlconsumption dlconsumption_f in 4/7
*-- 多步预测: dynamic()选项+step()选项
use http://www.stata-press.com/data/r11/lutkepohl2,clear
var dlinvest dlincome dlconsumption,lag(1/2) dfk small
varfcast compute, dynamic(85) step(10)
list dlinvestment dlinvestment_f dlincome dlincome_f ///
dlconsumption dlconsumption_f in 83/95
4.7 结构型的VAR模型
前面讲的缩减型VAR模型只能描述各个内生变量的动态形成过程；着重的是内生变量的“跨期”相关性，并不考虑内生变量的“同期”相关性，因此无法呈现内生变量之间的“因果关系”。而且在脉冲响应函数和方差分解中是采用Choleski分解，硬性地规定上面所说的B矩阵对角线的上半部分为零。而采用结构型VAR模型(SVAR)，则可以根据相关理论设定变量之间的因果关系，从标准型(也即缩减型)VAR方程得到的残差分解出各个内生变量独立的残差(也即新息)。所以在结构型VAR模型中，最重要的一点就是要判断我们所分析的经济变量中，根据经济理论，确定它们之间当期的因果，那些当期没有因果关系的我们就设定约束条件令为0，同时约束条件的个数跟标准型VAR模型的Choleski分解所要限定的约束条件的个数(n^2-n)/2是一样的。
实例：
根据美国的投资、收入、消费的数据，我们设定了结构型VAR模型：
模型 y_t = (dlinvestment, dlincome, dlcosumption)'
设
| 1 0 0 | | . 0 0 |
A = | . 1 0 | B = | 0 . 0 |
| . . 1 | | 0 0 . |
含义：
(1) 当期投资(invest)不受收入(income)和消费(consumption)的影响
(2) 收入(income)受当期投资(invest)的影响，但不受当期消费(consumption)的影响
(3) 消费(consumption)同时受到当期投资(invest)和收入(income)的影响
其中：
(1) A 的系数反映了各个内生变量的同期关系，即因果关系；
(2) B 的系数反映了来自不同内生变量的随机干扰对系统的影响
程序：
use http://www.stata-press.com/data/r11/lutkepohl2,clear
mat A = (1,0,0 \ .,1,0 \ .,.,1)
mat B = (.,0,0 \ 0,.,0 \ 0,0,.)
mat list A
mat list B
svar dlinvestment dlincome dlconsumption, aeq(A) beq(B)
est store svar01
mat list e(A)
mat list e(B)
下面就得到了A、B矩阵的系数：
e(A)[3,3]
dlinvestment dlincome dlconsumpt~n
dlinvestment 1 0 0
dlincome -.03136105 1 0
dlconsumpt~n -.05667905 -.47924065 1
symmetric e(B)[3,3]
dlinvestment dlincome dlconsumpt~n
dlinvestment .04251726
dlincome 0 .01069078
dlconsumpt~n 0 0 .00744606
有时我们可以在做结构型VAR模型的估计过程，将原先的标准型VAR模型的估计给呈现出来：
svar dlinvestment dlincome dlconsumption, aeq(A) beq(B) var
对于进行模型检验、脉冲响应、方差分解和格兰杰因果检验的方法以及判断准则跟上面的标准型VAR模型的做法是一样的。有点要注意的是，假如要进行结构脉冲响应和方差分解，则只需将原来的命令改为 sirf、sfevd就行了。