1、目的

顾名思义，集成算法就是把多个算法的结果汇总起来，以期得到更好的效果。
常见的集成算法模型有：Bagging、Boosting、Stacking。下面对三种模型进行详细的介绍。

2、Bagging

Bagging全称是bootstrap aggregation，基本思想是训练多个分类器，各个分类器之间不存在强依赖关系，然后把计算结果求平局值：$f(x)=1/M{\sum }_{m=1}^m{f}_m(x)$。

• $f_m(x)$代表第m个分类器。
• 整个公式的含义就是各个分类器平局值。

随机森林是这一模型的典型代表。

2.1 随机森林的定义

随机的含义是：数据采样随机，特征选择随机。
森林的含义是：一群决策树并行放在一起。
所以随机森林就是随机采样、随机特征形成的一堆决策树，并行进行计算，然后对计算结果求平局值得到最终的结果。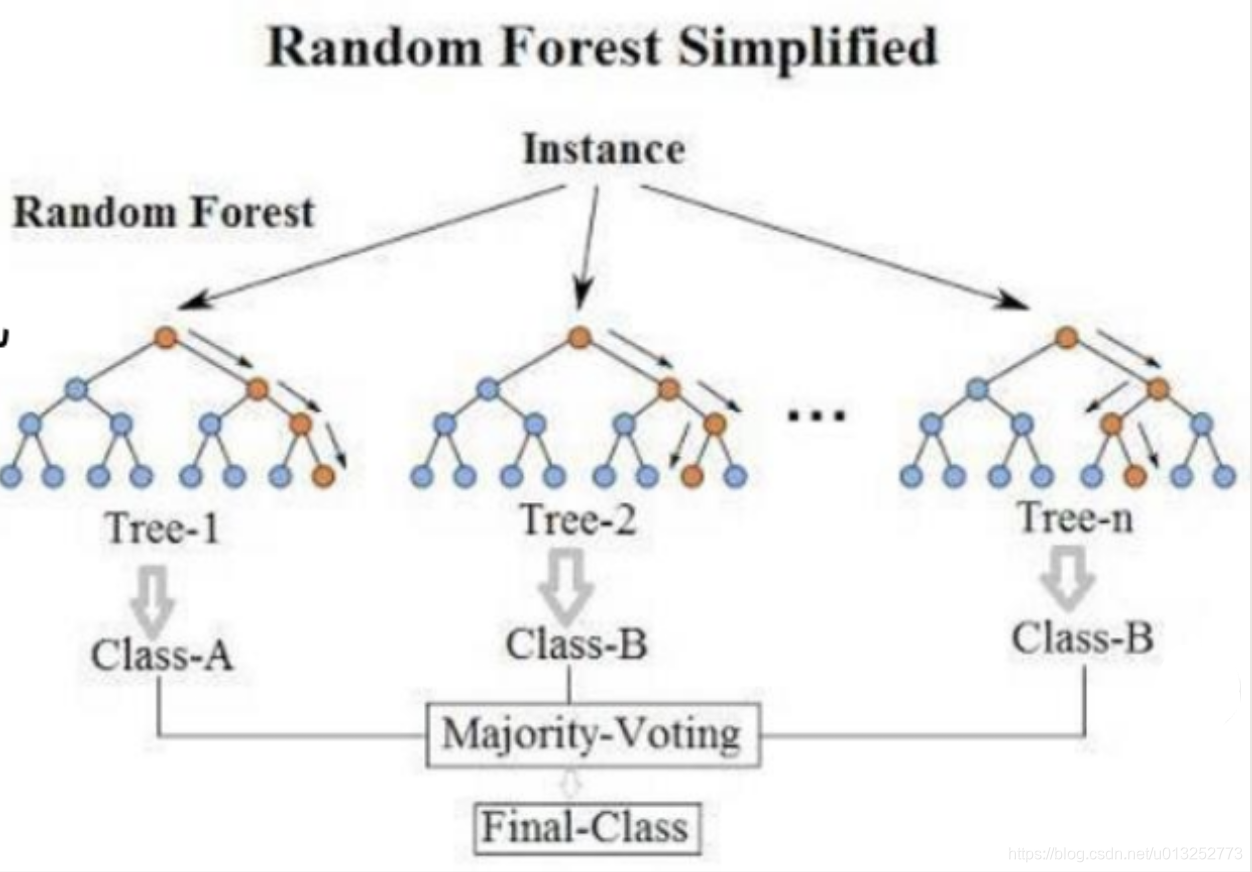

2.2 随机森林的构建

随机森林每个决策树的构建，都满足两个条件：随机采样、随机选择特征。只有这样，才能保证各个决策树计算出来的结果，拥有足够的泛化能力。
随机森林构建完成后，对于分类任务和回归任务的结果处理也有不同：

• 分类任务：最终结果等于多数分类器的结果。
• 回归任务：最终结果等于分类器结果的平均。

决策树的数量

构成随机森林的决策树数量越多，效果不一定越好。如下图所示，数量为80时，效果要好于数量为90时，所以需要根据实际的情况对结果进行判断：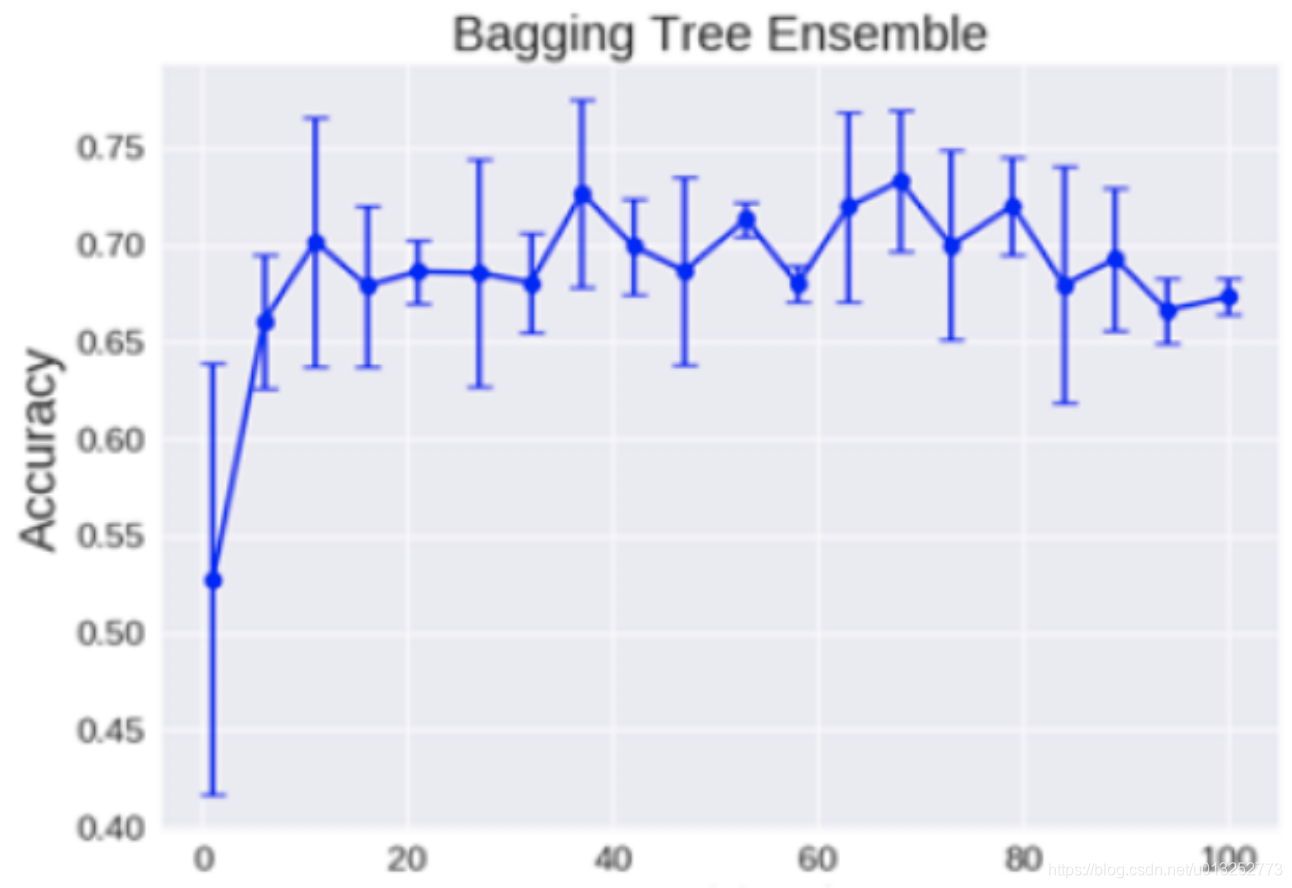

2.3 随机森林的优缺点

优点

• 处理高纬度数据，且不用选定特征：因为特征是随机选择的。
• 计算完成后，可以给出特征的重要程度。
• 可以做出并行方法，运算速度快。
• 可以进行可视化展示，便于分析。

缺点

• 解决回归问题时，不能给出连续的输出，造成效果可能不好。
• 计算过程是个黑盒子，只能调整参数来改变结果，可解释性差。

3、Boosting

典型代表是AdaBoost、XgBoost算法。
基本思想是“逐步强化”。计算过程为：

• 所有样本权重相同，训练得到第一个弱分类器。
• 根据上一轮的分类效果，调整样本的权重，上一轮分错的样本权重提高，重新进行训练。
• 重复以上步骤，直到达到约定的轮数结束。
• 由于处于分类边界的点容易分错，因此会得到更高的权重。

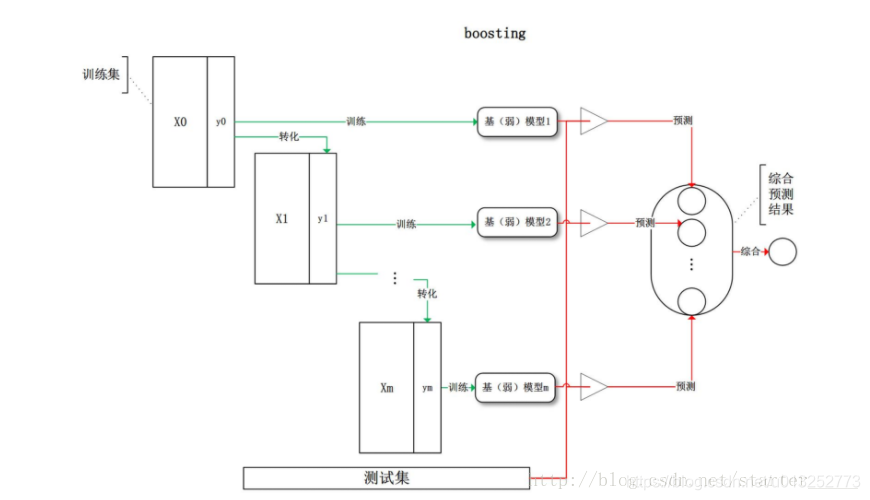
疑问：有的说是对样本改变权重，有的说是对分类器改变权重，究竟哪个是对的？？

4、Stacking

该算法的基本思想是：把样本分成n份，使用n个分类器对样本进行计算；计算的结果作为下一层分类器的输入；不断迭代，直到达到迭代的次数限制为止。
缺点：效率非常低。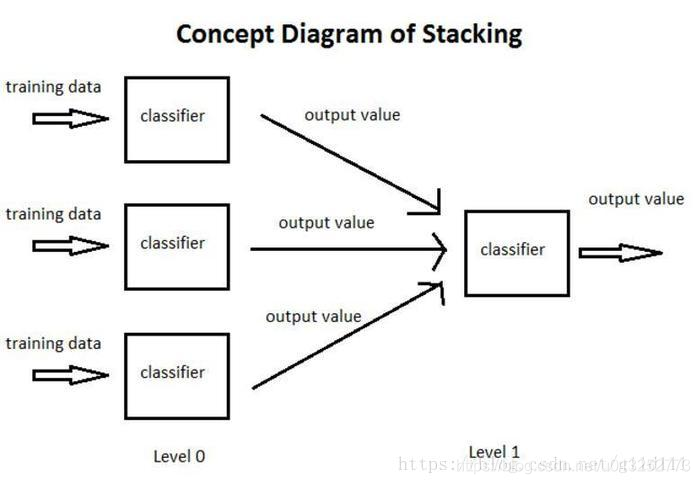

参考文档

Boosting学习笔记（Adboost、GBDT、Xgboost）
机器学习 —— Boosting算法
机器学习算法——集成方法（Ensemble）之Stacking