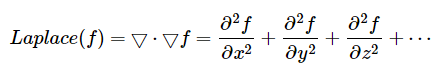了解拉普拉斯算子
1. Laplace算子的定义
直奔主题:Laplace算子被定义为函数梯度的散度,即:
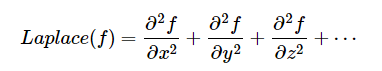
在图像处理,我们知道经常把Laplace算子作为边缘检测之一,也是工程数学中常用的一种积分变换。
- 梯度:
假设在空间坐标系下,那么一个函数 f(x,y,z) 在点 (x0 , y0 ,z0) 处的梯度定义如下:
▽ f = ( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ) ∣ x = x 0 , y = y 0 , z = z 0 \bigtriangledown f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})|_{x=x_{0},y=y_{0},z=z_{0}}▽f=(∂x∂f,∂y∂f,∂z∂f)∣x=x0,y=y0,z=z0
于是梯度函数:▽ f = ∂ f ∂ x ⋅ i ⃗ + ∂ f ∂ y ⋅ j ⃗ + ∂ f ∂ z ⋅ k ⃗ \bigtriangledown f=\frac{\partial f}{\partial x}\cdot \vec{i}+\frac{\partial f}{\partial y}\cdot \vec{j}+\frac{\partial f}{\partial z}\cdot \vec{k}▽f=∂x∂f⋅i+∂y∂f⋅j+∂z∂f⋅k
- 散度:
假设在空间坐标系下,若函数 F ( x , y , x ) = F x ⋅ i ⃗ + F y ⋅ j ⃗ + F z ⋅ k ⃗ F(x,y,x)=F_{x}\cdot \vec{i}+F_{y}\cdot \vec{j}+F_{z}\cdot \vec{k}F(x,y,x)=Fx⋅i+Fy⋅j+Fz⋅k ,那么其散度定义如下:
d i v F = ▽ ⋅ F = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z div\ F=\bigtriangledown \cdot F=\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}+\frac{\partial F_{z}}{\partial z}div F=▽⋅F=∂x∂Fx+∂y∂Fy+∂z∂Fz
- Laplace算子:
2. 转换成离散形式
在图像处理领域,由于图像有x和y两个方向,且是离散分布的,需要将Laplace算子方程表示为其在x,y两个方向的离散形式:
- 离散一阶微分方程: ∂ f ∂ x = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x}=f(x+1)-f(x)∂x∂f=f(x+1)−f(x)
- 离散二阶微分方程: ∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^2 f}{\partial x^2}=f(x+1)+f(x-1)-2f(x)∂x2∂2f=f(x+1)+f(x−1)−2f(x)
- Laplace算子离散方程:
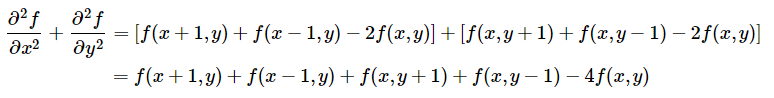
转换成卷积核表示如下:
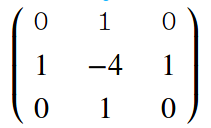
版权声明:本文为qq_40520596原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。