快速排序与其性能分析

1 快速排序的描述

快速排序是采用的分治策略，例如对子数组$A[p:r]$进行快速排序的三步分治过程如下：
分解：数组$A[p:r]$被划分为两个子数组$A[p:q-1]$和$A[q+1..r]$，使得$A[p:q-1]$中每一个元素都小于$A[q]$，$A[p+1:r]$中每一个元素都大于$A[q]$。
解决：通过递归调用快速排序，对子数组$A[p:q-1]$和$A[q+1..r]$进行排序。
合并：原址排序并不需要合并。（原址排序指不需要额外的空间就可完成排序）
快速排序的伪代码如下：
QUICKSORT(A, p, r)

if p<r:
	q = PARITITION(A,p,r)
	QUICKSORT(A,p,q-1)
	QUICKSORT(A,q+1, r)

排序整个数组$A$应该调用QUICKSORT(A, 1, A.length)。
数组的划分使用的ARITITION过程，对A[p…r]实现原址重排。
PARTITION(A, p, r)

x = A[r]
i = p-1
for j=p to r-1
	if A[j] <= x
		i+=1
		exchange A[i] with A[j]
exchange A[i+1] with A[r]
return i + 1

PARTITION(A, p, r)的功能是，重新排序数组$A$，并返回p，使得$A[:q-1]$中每一个元素都小于$A[q]$，$A[p+1:]$中每一个元素都大于$A[q]$。上述伪代码总是选择$x=A[r]$作为主元（即为最终的A[p]），并围绕着这个元素划分子数组。PARTITION过程如下图：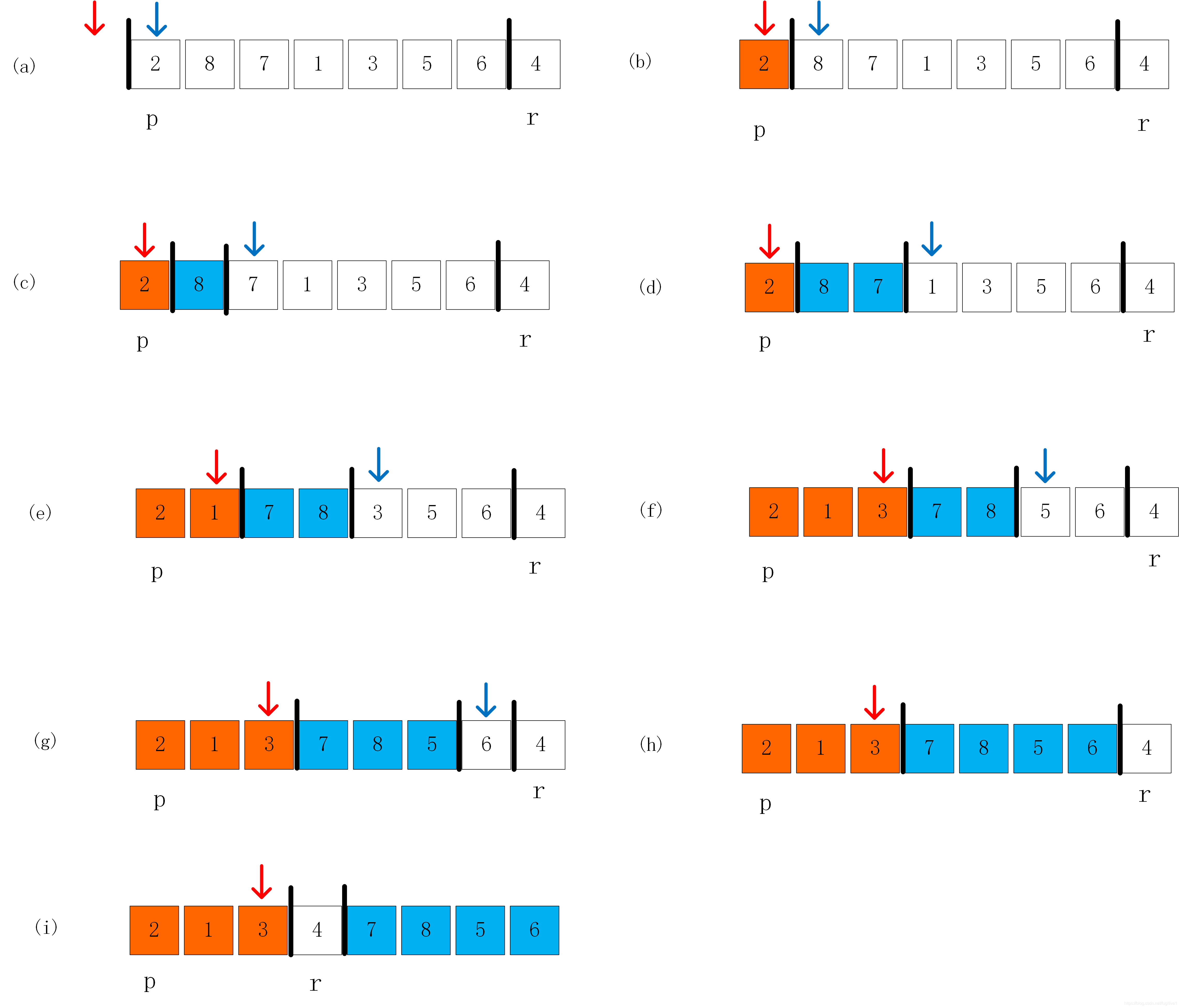

图中红色部分是小于主元的，蓝色是大于主元部分，红色箭头代表PARTITION(A, p, r)中的i，蓝色箭头代表PARTITION(A, p, r)中的j，白色是PARTITION(A, p, r)中的x。PARTITION操作的正确性在算法导论中用循环不变式进行证明，这里就不多说了。

2 快速排序的性能

快速排序的运行时间，与其划分是否平衡有关系，划分越不平衡则性能越差，最坏接近插入排序（$O(n^2)$），划分平衡则性能与归并排序($O(nlgn)$)一样。

2.1 最坏情况

当每次划分产生的子问题分别包含了，$n-1$个元素和$0$个元素时，这时候快速排序的最坏情况发生了，假设每一步都是这样子不均衡。若此时将时间表示为$T(n)$，那么有递归式：$T(n)=T(n-1)+T(0)+\Theta (n)$，其中：$T(n-1)$是划分多的一边（$n-1$那一部分），$T(0)$为划分少的一边（$0$那一部分），$\Theta (n)$为划分$n$个元素所花费的时间。可以用带入法（之前的分治策略中有说明）求解此式子的结果为$\Theta (n^2)$。
因此在每一层都不平衡的情况下，运行时间为$\Theta (n^2)$，即在最坏情况下的快速排序运行时间并不比插入排序好，在输入数组有序的情况下，若采用上述PARTITION操作的话，快速排序的复杂度仍为$\Theta (n^2)$。但是插入排序在这种情况下是$\Theta (n)$。

2.2 最好情况

最好情况下，PARTITION操作之后的两个字问题的规模都不大于$\frac{n}{2}$.在这种情况下，快速排序的性能非常好。此时有递归式：$T(n)=2T(\frac{n}{2})+\Theta (n)$；根据主定理（主定理可以参考前面的分治策略）的情况2求得递归式解为$T(n)=\Theta (nlgn)$。

2.3 平衡划分情况

假设划分算法总是产生9:1的划分，看起来是很不平衡的，此时的递归式为：$T(n)=T(\frac{9n}{10})+T(\frac{n}{10})+cn$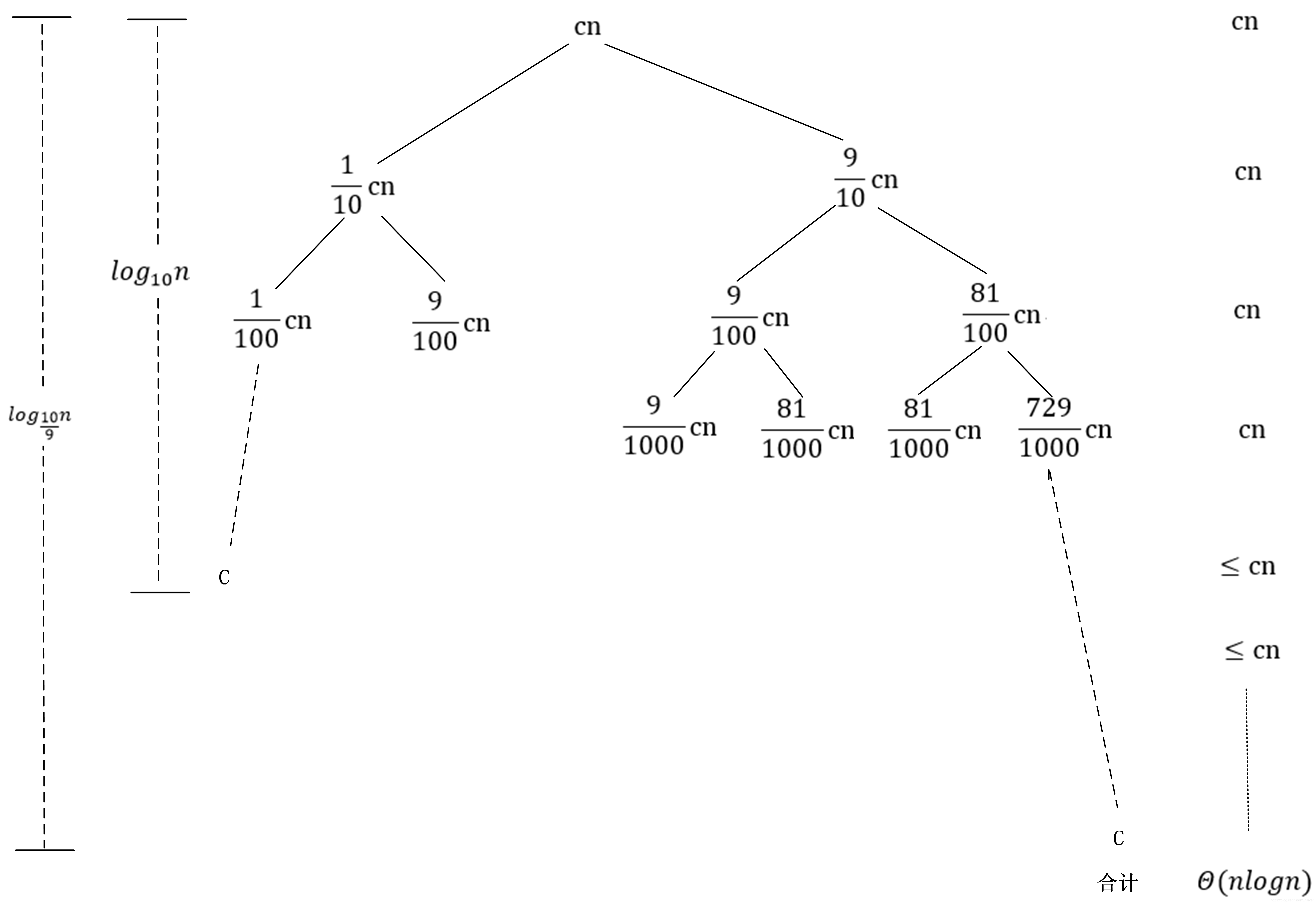

上图是递归式$T(n)$的递归树，其特点是每个左子节点都是占比为1，右子节点占比为9，因此导致最左边的树枝最短，长度为：$lo{g}_{10}n$，最右边的树枝最长，长度为：$lo{g}_{\frac{10}{9}}n$。最短这边的长度计算过程为：若$cn$每一次是之前的$\frac{1}{10}$，设其长度为$h$则有$(\frac{1}{10}{)}^h\ast cn=c$，即划分了$h$次最终到了$c$，解得$h=lo{g}_{10}n$；同理长的这一边有$(\frac{9}{10}{)}^h\ast cn=c$，解得$h=lo{g}_{\frac{10}{9}}n$。
由上图可知，对于这种划分的运行时间$T(n)$有：$cnlo{g}_{10}n<T(n)<cnlo{g}_{\frac{10}{9}}n$，其中:$cnlo{g}_{10}n=c\ast lo{g}_{10}2\ast nlo{g}_{2}n=\Theta (nlgn)$，$cnlo{g}_{\frac{10}{9}}n=c\ast lo{g}_{\frac{10}{9}}2\ast nlo{g}_{2}n=\Theta (nlgn)$。因此这种划分的时间仍然是$\Theta (nlgn)$，看起来$1:9$的划分已经相当不平衡了，但是其时间仍为$\Theta (nlgn)$，事实上，任意常数比例划分的时间均为$\Theta (nlgn)$。

3 总结

本篇博客根据《算法导论》详细的介绍了快速排序，以及分析了在最坏、最好、以及“正常”情况下的性能，但是未考虑平均或随机的情况。