Problem 1. Lonely Photo
(Analysis by Nick Wu)
We need to count the number of substrings of length 3 that contain exactly one G or one H.
The most direct solution involves checking every substring of length at least 3. There are O(N^2) such substrings to check, and each one takes O(N) time to validate, for a total runtime of O(N^3).
To improve the performance of this solution, we can choose to check substrings in a specific order. In particular, fix the leftmost character in the substring and then start scanning to the right. If we have seen at least three characters and exactly one of them is G or one of them is H, increment a counter. Loop over all leftmost characters and then print the counter at the end. The approach of this solution is O(N^2).
#include <iostream>
#include <string>
int main() {
int n;
std::string s;
std::cin >> n >> s;
int ans = 0;
for(int i = 0; i < (int)s.size(); i++) {
int g = 0;
int h = 0;
for(int j = i; j < (int)s.size(); j++) {
if(s[j] == 'G') g++;
else h++;
if(g+h >= 3 && (g==1 || h==1)) ans++;
}
}
std::cout << ans << "\n";
}It is possible to solve this problem in O(N). For each character, let's count the number of photos in which that character is the odd one out. In the case where that character is G, the substring must either have at least two H's on one side of it or at least one H on both sides of it and no other occurrences of G. We can count the number of mismatching characters directly to the left and to the right and account for both cases.
#include <iostream>
#include <string>
using namespace std;
int main() {
int n;
string s;
cin >> n >> s;
int64_t ans = 0;
for(int i = 0; i < n; i++) {
int64_t lhs = 0;
if(i > 0 && s[i-1] != s[i]) {
lhs++;
for(int k = i-2; k >= 0 && s[k] == s[i-1]; k--) lhs++;
}
int64_t rhs = 0;
if(i+1 < n && s[i+1] != s[i]) {
rhs++;
for(int k = i+2; k < n && s[k] == s[i+1]; k++) rhs++;
}
ans += lhs * rhs + max(lhs-1, (int64_t)0) + max(rhs-1, (int64_t)0);
}
cout << ans << "\n";
}Problem 2. Air Cownditioning
(Analysis by Benjamin Qi and Nick Wu)
We'll start by defining di=pi−ti for all i in 1…N. Note that di is therefore the amount the temperature needs to change for cow i to be happy. Now, instead of making pi=ti, we can focus on making di zero. Note that, just as we can increase or decrease all values in some subsegment of tt by 1, we can increase or decrease all values in some subsegment of d by 1.
How do we make d zero everywhere making as few changes as possible? Intuitively, we want to avoid increasing values of dd that are already positive or decreasing values of d that are already negative. We also don't want to touch values of d that are zero.
One strategy that we might try therefore is as follows - assuming that dN is positive, find the smallest j such that dj through dN are all positive, and then decrease all those numbers by one. If dN is negative, we apply similar logic except we increase as many negative numbers as possible by one. In other words, find the longest suffix where all numbers are positive or all numbers are negative, and then adjust all of them towards zero.
Ben's code:
#include <bits/stdc++.h>
using namespace std;
int main() {
int N;
cin >> N;
vector<int> p(N), t(N), d(N);
for (int i = 0; i < N; ++i)
cin >> p[i];
for (int i = 0; i < N; ++i)
cin >> t[i];
for (int i = 0; i < N; ++i)
d[i] = p[i] - t[i];
int first_nonzero = 0, ans = 0;
while (true) {
while (first_nonzero < N && d[first_nonzero] == 0)
++first_nonzero;
if (first_nonzero == N)
break;
int r = first_nonzero;
auto sgn = [&](int x) {
if (x < 0)
return -1;
if (x > 0)
return 1;
return 0;
};
while (r + 1 < N && sgn(d[r + 1]) == sgn(d[first_nonzero]))
++r;
for (int i = first_nonzero; i <= r; ++i) {
if (d[i] < 0)
++d[i];
else
--d[i];
}
++ans;
}
cout << ans << "\n";
}These two solutions are O(N⋅V), where V is the maximum possible value in d. Under the given bounds though, the answer can be as large as one billion, so we need to do better than simulating this step by step.
One thing worth trying that does pass all test cases is, instead of just incrementing or decrementing by one, doing as many increments/decrements as possible until some element becomes zero.
We can do provably better though - in particular, we can solve this problem in O(N).
We'll add a zero to the beginning and end of dd - specifically, we'll define d0=dN+1=0d0=dN+1=0. This does not change the answer, as we never need to change any zeroes. We'll also define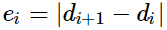 
- that is, the difference between adjacent values of didi. Why is ei important? If ei is zero, then di and di+1 are the same and any operation we do to di should also be done to di+1. However, if ei is large, then the two values are very different, and there must be at least ei operations that take place on one of di and di+1 but not the other.
More specifically, when we increase the range of values di through dj, note that ei−1 and ej change by one each, and all other values in e remain unchanged. This motivates the following claim.
Claim: The answer is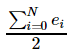 
, or half the sum of all the values in ee.
Proof: The sum of all values of ee equals zero if and only if all didi are zero. Furthermore, every command changes this quantity by at most 2. This shows that the answer is at least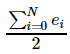 
To show that this answer is attainable, any number of greedy strategies suffice. One valid strategy is the one we had above - find the longest suffix of all positive or all negative integers, and adjust them towards zero by one.
We can evaluate the formula mentioned above in O(N) time.
Ben's code:
#include <bits/stdc++.h>
using namespace std;
int main() {
int N;
cin >> N;
vector<int> p(N + 1), t(N + 1), d(N + 2);
for (int i = 1; i <= N; ++i)
cin >> p[i];
for (int i = 1; i <= N; ++i)
cin >> t[i];
for (int i = 1; i <= N; ++i)
d[i] = p[i] - t[i];
int ans = 0;
for (int i = 0; i <= N; ++i)
ans += abs(d[i] - d[i + 1]);
cout << ans / 2;
}