6 拉普拉斯变换
6.1 基本概念
拉普拉斯变换的定义
拉普拉斯变换 LT
F ( s ) = L [ f ( s ) ] = ∫ 0 ∞ f ( t ) e − s t d t F(s)=L[f(s)]=\int_0^\infty f(t)e^{-st}dtF(s)=L[f(s)]=∫0∞f(t)e−stdt
拉普拉斯逆变换 ILT
f ( t ) = L − 1 [ F ( s ) ] f(t)=L^{-1}[F(s)]f(t)=L−1[F(s)]
F ( s ) F(s)F(s) 在某一区域内收敛, F ( s ) F(s)F(s) 称为象函数, f ( t ) f(t)f(t) 称为象原函数。
LT 存在定理
若复值函数 f ( t ) f(t)f(t) 满足下列条件:
(1) 在 t ≥ 0 t\geq0t≥0 的任意有限区间上分段连续;
(2) 当 t → + ∞ t\rightarrow+\inftyt→+∞ 时, f ( t ) f(t)f(t) 的增长速度不超过某一指数函数,即存在常数 M > 0 M>0M>0 及 σ 0 ≥ 0 \sigma_0\geq0σ0≥0 ,使得
∣ f ( t ) ∣ ≤ M e σ 0 t ( t ≥ 0 ) |f(t)|\leq Me^{\sigma_0t}\ \ \ \ \ \ (t\geq0)∣f(t)∣≤Meσ0t (t≥0)
则 L [ f ( t ) ] L[f(t)]L[f(t)] 在半平面 R e ( s ) > σ 0 {\rm Re}(s)>\sigma_0Re(s)>σ0 上存在且解析, σ 0 \sigma_0σ0 称为函数 f ( t ) f(t)f(t) 的增长指数。
注意:LT 存在定理的条件是充分不必要条件。
说明:
设 σ = R e ( s ) \sigma = {\rm Re}(s)σ=Re(s) , σ − σ 0 ≥ δ > 0 \sigma-\sigma_0\geq\delta>0σ−σ0≥δ>0 ,由条件 (2) 可知,对于任何 t ≥ 0 t\geq0t≥0 ,有
∣ f ( t ) e − s t ∣ = ∣ f ( t ) ∣ e − σ t ≤ M e − ( σ − σ 0 ) t ≤ M e − δ t |f(t)e^{-st}|=|f(t)|e^{-\sigma t}\leq Me^{-(\sigma-\sigma_0)t}\leq Me^{-\delta t}∣f(t)e−st∣=∣f(t)∣e−σt≤Me−(σ−σ0)t≤Me−δt
所以
∫ 0 ∞ ∣ f ( t ) e − s t ∣ d t ≤ M ∫ 0 ∞ e − δ t d t = M δ \int_0^{\infty}|f(t)e^{-st}|dt \leq M\int_0^{\infty}e^{-\delta t}dt=\frac{M}{\delta}∫0∞∣f(t)e−st∣dt≤M∫0∞e−δtdt=δM
即积分 ∫ 0 ∞ f ( t ) e − s t d t \displaystyle\int_0^\infty f(t)e^{-st}dt∫0∞f(t)e−stdt 在 R e ( s ) ≥ σ 0 + δ {\rm Re}(s)\geq\sigma_0+\deltaRe(s)≥σ0+δ 上绝对且一致收敛,且 F ( s ) = ∫ 0 ∞ f ( t ) e − s t d t F(s)=\displaystyle\int_0^\infty f(t)e^{-st}dtF(s)=∫0∞f(t)e−stdt 存在。
Γ \GammaΓ 函数和 B e t a BetaBeta 函数
Γ \GammaΓ 函数是工程中常用的特殊函数,其定义为
Γ ( a ) = ∫ 0 ∞ t a − 1 e − t d t ( a > 0 ) \Gamma(a)=\int_0^\infty t^{a-1}e^{-t}dt \ \ \ \ (a>0)Γ(a)=∫0∞ta−1e−tdt (a>0)Γ ( n + 1 ) = n ! ( n ∈ N ) \Gamma(n+1)=n! \ \ \ \ (n\in N)Γ(n+1)=n! (n∈N)
B \BetaB 函数是工程中常用的特殊函数,其定义为
B ( α , β ) = ∫ 0 1 t α − 1 ( 1 − t ) β − 1 d t ( α , β > 0 ) \Beta(\alpha,\,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt \ \ \ \ (\alpha,\,\beta>0)B(α,β)=∫01tα−1(1−t)β−1dt (α,β>0)B ( α , β ) = Γ ( α ) Γ ( β ) Γ ( α + β ) \Beta(\alpha,\,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}B(α,β)=Γ(α+β)Γ(α)Γ(β)
函数 f ( t ) = t a ( a > − 1 ) f(t)=t^a\ \ (a>-1)f(t)=ta (a>−1) 的拉普拉斯变换为
L [ t a ] = Γ ( a + 1 ) s a + 1 L[t^a]=\frac{\Gamma(a+1)}{s^{a+1}}L[ta]=sa+1Γ(a+1)
特别地,当 a aa 是非负整数 n nn 时,
L [ t n ] = n ! s n + 1 L[t^n]=\frac{n!}{s^{n+1}}L[tn]=sn+1n!
6.2 基本性质
假定:象原函数 f ( t ) f(t)f(t) 都满足 LT 存在定理的条件,且象函数 F ( s ) F(s)F(s) 的自变量 s ss 满足 R e ( s ) = σ > σ 0 {\rm Re}(s)=\sigma>\sigma_0Re(s)=σ>σ0 。
线性性质
L [ α 1 f 1 ( t ) + α 2 f 2 ( t ) ] = α 1 F 1 ( s ) + α 2 F 2 ( s ) L[\alpha_1f_1(t)+\alpha_2f_2(t)]=\alpha_1F_1(s)+\alpha_2F_2(s)L[α1f1(t)+α2f2(t)]=α1F1(s)+α2F2(s)
L − 1 [ α 1 F 1 ( s ) + α 2 F 2 ( s ) ] = α 1 f 1 ( t ) + α 2 f 2 ( t ) L^{-1}[\alpha_1F_1(s)+\alpha_2F_2(s)]=\alpha_1f_1(t)+\alpha_2f_2(t)L−1[α1F1(s)+α2F2(s)]=α1f1(t)+α2f2(t)
平移性质
(1) 时移性质
若 L [ f ( t ) ] = F ( s ) L[f(t)]=F(s)L[f(t)]=F(s) , f ( t ) ≡ 0 ( t < 0 ) f(t)\equiv 0\ \ (t<0)f(t)≡0 (t<0) ,则对于 t 0 > 0 t_0>0t0>0 ,有
L [ f ( t − t 0 ) ] = e − s t 0 F ( s ) L[f(t-t_0)]=e^{-st_0}F(s)L[f(t−t0)]=e−st0F(s)
L − 1 [ e − s t 0 F ( s ) ] = f ( t − t 0 ) L^{-1}[e^{-st_0}F(s)]=f(t-t_0)L−1[e−st0F(s)]=f(t−t0)
因为 t < 0 t<0t<0 时, f ( t ) ≡ 0 f(t)\equiv0f(t)≡0 ,所以 t < t 0 t<t_0t<t0 时, f ( t − t 0 ) ≡ 0 f(t-t_0)\equiv0f(t−t0)≡0 ,故上式中的 f ( t − t 0 ) f(t-t_0)f(t−t0) 也可以写为 f ( t − t 0 ) u ( t − t 0 ) f(t-t_0)u(t-t_0)f(t−t0)u(t−t0) 。
其中 u ( t ) u(t)u(t) 为单位阶跃函数
u ( t ) = { 0 , t < 0 1 , t > 0 u(t)= \left\{ \begin{array}{lll} 0 &, & t<0\\ 1 &, & t>0 \end{array} \right.u(t)={01,,t<0t>0
函数 f ( t − t 0 ) f(t-t_0)f(t−t0) 与 f ( t ) f(t)f(t) 相比, f ( t ) f(t)f(t) 从 t = 0 t=0t=0 开始有非零数值,而 f ( t − t 0 ) f(t-t_0)f(t−t0) 从 t = t 0 t=t_0t=t0 开始
周期函数 f ( t ) = f ( t + T ) f(t)=f(t+T)f(t)=f(t+T) 的拉普拉斯变换
f 1 ( t ) = { f ( t ) , 0 < t < T 0 , 其他 f_1(t)= \left\{ \begin{array}{cll} f(t) &, & 0<t<T\\ 0 &, & \text{其他} \end{array} \right.f1(t)={f(t)0,,0<t<T其他F 1 ( t ) = ∫ 0 T f 1 ( t ) e − s t d t F_1(t)=\int_0^Tf_1(t)e^{-st}dtF1(t)=∫0Tf1(t)e−stdt
则 f ( t ) = f 1 ( t ) + f 1 ( t − T ) + f 1 ( t − 2 T ) + . . . f(t)=f_1(t)+f_1(t-T)+f_1(t-2T)+...f(t)=f1(t)+f1(t−T)+f1(t−2T)+...
F ( s ) = ∫ 0 ∞ f ( t ) e − s t d t = F 1 ( s ) + F 1 ( s ) e − s T + F 1 ( s ) e − 2 s T + . . . = F 1 ( s ) 1 1 − e − s T F(s)=\int_0^\infty f(t)e^{-st}dt=F_1(s)+F_1(s)e^{-sT}+F_1(s)e^{-2sT}+...=F_1(s)\frac{1}{1-e^{-sT}}F(s)=∫0∞f(t)e−stdt=F1(s)+F1(s)e−sT+F1(s)e−2sT+...=F1(s)1−e−sT1
(2) 频移性质
若 L [ f ( t ) ] = F ( s ) L[f(t)]=F(s)L[f(t)]=F(s) ,则对于任意常数 s 0 s_0s0 ,有
L [ e s 0 t f ( t ) ] = F ( s − s 0 ) L[e^{s_0t}f(t)]=F(s-s_0)L[es0tf(t)]=F(s−s0)
L − 1 [ F ( s − s 0 ) ] = e s 0 t f ( t ) L^{-1}[F(s-s_0)]=e^{s_0t}f(t)L−1[F(s−s0)]=es0tf(t)
微分性质
(1) 象原函数的微分性质
若 L [ f ( t ) ] = F ( s ) L[f(t)]=F(s)L[f(t)]=F(s) ,且 f ′ ( t ) f'(t)f′(t) 也是象原函数,则
L [ f ′ ( t ) ] = s F ( s ) − f ( 0 + ) L[f'(t)]=sF(s)-f(0^+)L[f′(t)]=sF(s)−f(0+)
若 f ( k ) ( t ) ( k = 1 , 2 , . . . , n ) f^{(k)}(t)\ \ (k=1,2,...,n)f(k)(t) (k=1,2,...,n) 是象原函数,则
L [ f ( n ) ( t ) ] = s n F ( s ) − s n − 1 f ( 0 + ) − s n − 2 f ′ ( 0 + ) − . . . − f ( n − 1 ) ( 0 + ) L[f^{(n)}(t)]=s^nF(s)-s^{n-1}f(0^+)-s^{n-2}f'(0^+)-...-f^{(n-1)}(0^+)L[f(n)(t)]=snF(s)−sn−1f(0+)−sn−2f′(0+)−...−f(n−1)(0+)
特别地,当 f ( 0 ) = f ′ ( 0 ) = . . . = f ( n − 1 ) ( 0 ) = 0 f(0)=f'(0)=...=f^{(n-1)}(0)=0f(0)=f′(0)=...=f(n−1)(0)=0 时,有
L [ f ( n ) ( t ) ] = s n F ( s ) L[f^{(n)}(t)]=s^nF(s)L[f(n)(t)]=snF(s)
此性质可以使我们有可能将 f ( t ) f(t)f(t) 的微分方程转化为 F ( s ) F(s)F(s) 的代数方程。
(2) 象函数的微分性质
若 L [ f ( t ) ] = F ( s ) L[f(t)]=F(s)L[f(t)]=F(s) ,则
L [ ( − t ) n f ( t ) ] = F ( n ) ( s ) L[(-t)^nf(t)]=F^{(n)}(s)L[(−t)nf(t)]=F(n)(s)
L [ t n f ( t ) ] = ( − 1 ) n F ( n ) ( s ) L[t^nf(t)]=(-1)^nF^{(n)}(s)L[tnf(t)]=(−1)nF(n)(s)
积分性质:
若 L [ f ( t ) ] = F ( s ) L[f(t)]=F(s)L[f(t)]=F(s) ,则
L [ ∫ 0 t f ( u ) d u ] = 1 s F ( s ) L[\int_0^tf(u)du]=\frac{1}{s}F(s)L[∫0tf(u)du]=s1F(s)
若 L [ f ( t ) ] = F ( s ) L[f(t)]=F(s)L[f(t)]=F(s) ,且 ∫ s ∞ F ( u ) d u \displaystyle\int_s^\infty F (u)du∫s∞F(u)du 收敛,则
L [ f ( t ) t ] = ∫ s ∞ F ( u ) d u L[\frac{f(t)}{t}]=\int_s^\infty F(u)duL[tf(t)]=∫s∞F(u)du
6.3 卷积
卷积的定义:如果 ∫ − ∞ ∞ f 1 ( τ ) f 2 ( t − τ ) d τ \displaystyle\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau)d\tau∫−∞∞f1(τ)f2(t−τ)dτ 存在,则称它为函数 f 1 ( t ) f_1(t)f1(t) 与 f 2 ( t ) f_2(t)f2(t) 的卷积,记为
f 1 ( t ) ∗ f 2 ( t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( t − τ ) d τ f_1(t)*f_2(t)=\displaystyle\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau)d\tauf1(t)∗f2(t)=∫−∞∞f1(τ)f2(t−τ)dτ
卷积满足交换律、结合律、分配律。
在 LT 的计算中,有条件 f 1 ( t ) = f 2 ( t ) = 0 , ∀ t < 0 f_1(t)=f_2(t)=0\,,\ \forall t<0f1(t)=f2(t)=0, ∀t<0 ,则
f 1 ( t ) ∗ f 2 ( t ) = ∫ 0 t f 1 ( τ ) f 2 ( t − τ ) d τ f_1(t)*f_2(t)=\displaystyle\int_{0}^t f_1(\tau)f_2(t-\tau)d\tauf1(t)∗f2(t)=∫0tf1(τ)f2(t−τ)dτ
卷积定理
设 L [ f ( t ) ] = F ( s ) , L [ g ( t ) ] = G ( t ) L[f(t)]=F(s),\ L[g(t)]=G(t)L[f(t)]=F(s), L[g(t)]=G(t) ,则
L [ f ( t ) ∗ g ( t ) ] = F ( s ) ⋅ G ( s ) L[f(t)*g(t)]=F(s)\cdot G(s)L[f(t)∗g(t)]=F(s)⋅G(s)
L − 1 [ F ( s ) ⋅ G ( s ) ] = f ( t ) ∗ g ( t ) L^{-1}[F(s)\cdot G(s)]=f(t)*g(t)L−1[F(s)⋅G(s)]=f(t)∗g(t)
6.4 拉普拉斯逆变换
反演公式
若复值函数 f ( z ) f(z)f(z) 满足 LT 存在定理条件,则在 f ( t ) f(t)f(t) 的任意连续点处,都有
f ( t ) = 1 2 π i ∫ σ − i ∞ σ + i ∞ F ( s ) e s t d s f(t)=\frac{1}{2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty}F(s)e^{st}dsf(t)=2πi1∫σ−i∞σ+i∞F(s)estds
其中积分是沿着 S SS 平面上的任意一条直线 R e ( s ) = σ > σ 0 {\rm Re}(s)=\sigma>\sigma_0Re(s)=σ>σ0 的主值积分。 σ 0 \sigma_0σ0 是 f ( t ) f(t)f(t) 的增长指数。
若 F ( s ) F(s)F(s) 的全部奇点 s 1 , s 2 , . . . s n s_1,s_2,...s_ns1,s2,...sn 都在 R e ( s ) < σ {\rm Re}(s)<\sigmaRe(s)<σ 内,且 lim s → ∞ F ( s ) = 0 \displaystyle\lim_{s\to\infty}F(s)=0s→∞limF(s)=0 ,则 t > 0 t>0t>0 时,
f ( t ) = ∑ k = 1 n R e s [ F ( s ) e s t , s k ] f(t)=\sum_{k=1}^n{\rm Res}[F(s)e^{st},\,s_k]f(t)=k=1∑nRes[F(s)est,sk]
展开定理
如果函数 F ( s ) F(s)F(s) 在 ∞ \infty∞ 点处解析,且 lim s → ∞ F ( s ) = 0 \displaystyle\lim_{s\to\infty}F(s)=0s→∞limF(s)=0 ,即 F ( s ) F(s)F(s) 在 { s ; R < ∣ s ∣ < ∞ } \{s;R<|s|<\infty\}{s;R<∣s∣<∞} 内,其洛朗展开式为
F ( s ) = ∑ n = 0 ∞ a n s n + 1 F(s)=\sum_{n=0}^\infty \frac{a_{n}}{s^{n+1}}F(s)=n=0∑∞sn+1an
则
f ( t ) = L − 1 [ F ( s ) ] = ∑ n = 0 ∞ a n n ! t n f(t)=L^{-1}[F(s)]=\sum_{n=0}^\infty\frac{a_n}{n!}t^nf(t)=L−1[F(s)]=n=0∑∞n!antn
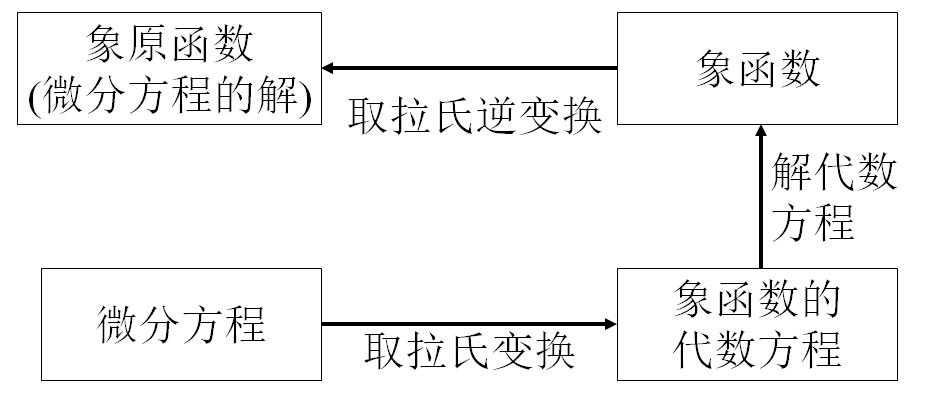
6.5 微分方程的拉氏变换解法
首先取拉氏变换将微分方程化为象函数的代数方程, 解代数方程求出象函数, 再取逆变换得最后的解.