Matlab求解LP问题
一、 调用 l i n p r o g linproglinprog 函数求解LP问题
m i n minmin f = c T X f=c^TXf=cTX
s . t . s.t.s.t. A X AXAX ≤ \leq≤ b bb
A e q X = b e q AeqX= beqAeqX=beq
l b lblb ≤ \leq≤ X XX ≤ \leq≤ u b ubub
式中,f , x , b , b e q , l b , u b f,x,b,beq,lb,ubf,x,b,beq,lb,ub 为向量;A , A e q A,AeqA,Aeq 为矩阵。
l i n p r o g linproglinprog函数的调用格式如下:
[ x , f v a l ] = l i n p r o g ( c , A , b , A e q , b e q , l b , u b ) [x,fval]= linprog(c,A,b,Aeq,beq,lb,ub)[x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
注:
- c cc 求解目标函数的系数矩阵
- A AA 不等式约束的系数矩阵
- b bb 不等式约束的系数矩阵
- A e q AeqAeq 等式约束的系数矩阵
- b e q beqbeq 等式约束相应的常数列向量,若没有等式约束,则均用 [ ] [][] 代替
- l b lblb 决策变量的下界,如果某个变量无下界,则用− i n f -inf−inf表示;若决策变量无下界,则用 [ ] [][] 或该参数可省
- u b ubub 决策变量的下界,如果某个变量无上界,则用i n f infinf
表示;若决策变量无下界,则用 [ ] [][]表示或者参数可省
例题:
m a x maxmax 3 x 1 − 5 x 2 3{x}_1-5{x}_23x1−5x2
s . t . s.t.s.t. − x 1 + 2 x 2 + 4 x 3 ≤ 4 -{x}_1+2{x}_2+4{x}_3\leq4−x1+2x2+4x3≤4
x 1 + x 2 + 2 x 3 ≤ 5 {x}_1+{x}_2+2{x}_3\leq5x1+x2+2x3≤5
− x 1 + 2 x 2 + x 3 ≥ 1 -{x}_1+2{x}_2+{x}_3\geq1−x1+2x2+x3≥1
x 1 , x 2 , x 3 ≥ 0 {x}_1,{x}_2,{x}_3\geq0x1,x2,x3≥0
分析:
原问题不符合求解LP的标准形式,需要做出一些变化,如下:
m i n minmin − 3 x 1 + 5 x 2 -3{x}_1+5{x}_2−3x1+5x2
s . t . s.t.s.t. − x 1 + 2 x 2 + 4 x 3 ≤ 4 -{x}_1+2{x}_2+4{x}_3\leq4−x1+2x2+4x3≤4
x 1 + x 2 + 2 x 3 ≤ 5 {x}_1+{x}_2+2{x}_3\leq5x1+x2+2x3≤5
x 1 − 2 x 2 − x 3 ≤ − 1 {x}_1-2{x}_2-{x}_3\leq-1x1−2x2−x3≤−1
x 1 , x 2 , x 3 ≥ 0 {x}_1,{x}_2,{x}_3\geq0x1,x2,x3≥0
clc
c = [-3, 5, 0];
A = [-1,2,4; 1,1,2; 1,-2,-1];
b = [4;5;-1];
Aeq = [];
beq = [];
lb = [0,0,0];
ub = [];
[x,fval]=linprog(c,A,b,Aeq,beq,lb) 结果如下: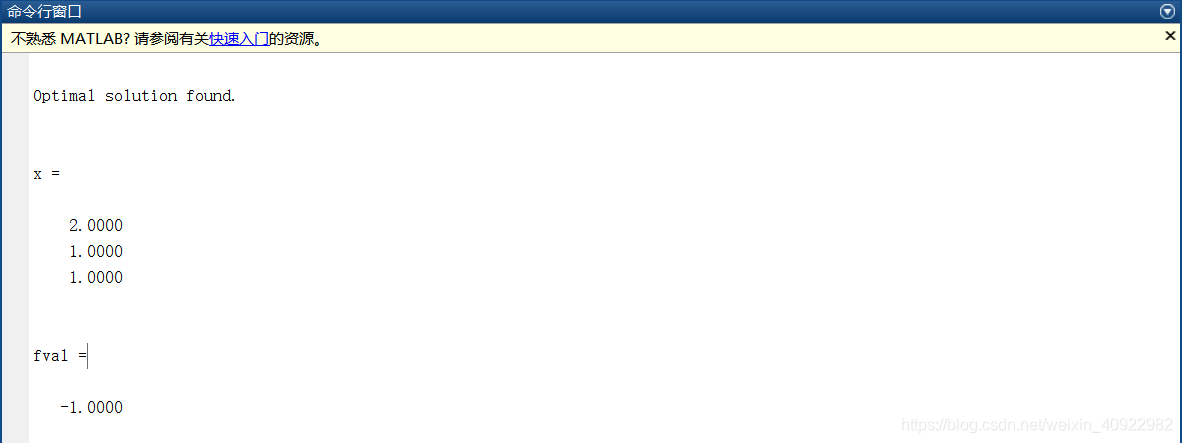
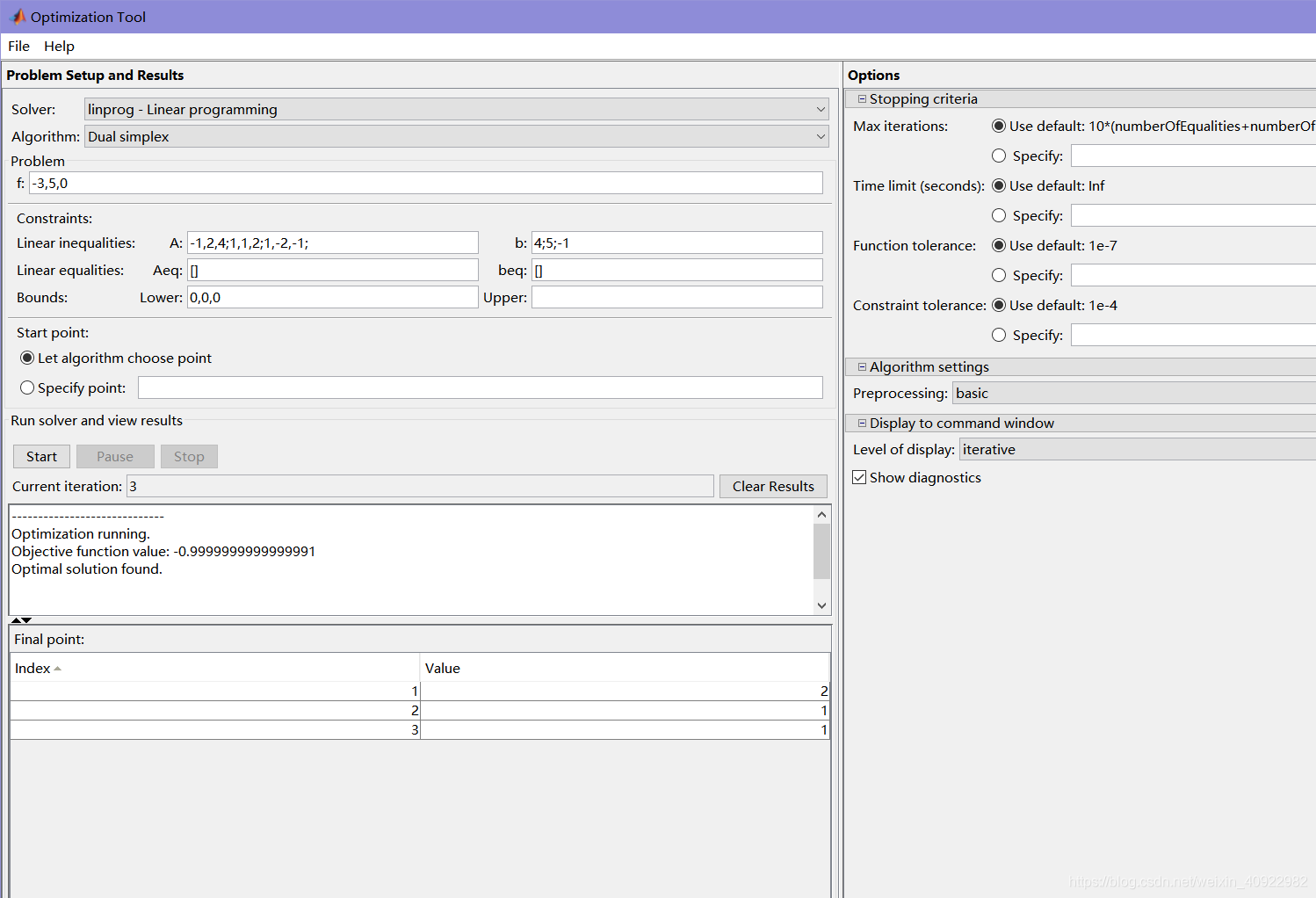
二、使用Matlab优化工具箱求解LP问题
在M a t l a b MatlabMatlab命令行输入o p t i m t o o l optimtooloptimtool或者在APP框下找到工具O p t i m i z a t i o n OptimizationOptimization打开,求解如下图: