概念
偏导数:是多个数(每元有一个);是指多元函数沿坐标轴方向的方向导数,因此二元函数就有两个偏导数。
偏导函数:是一个函数;是一个关于点的偏导数的函数。
方向导数:是一个数;反映的是f(x,y)在点沿方向v的变化率。
梯度:是一个向量;每个元素为函数对一元变量的偏导数;它既有大小(其大小为最大方向导数),也有方向。
0、导数:几何意义:当函数定义域和取值都在实数域中的时候,导数可以表示函数曲线上的切线斜率。 除了切线的斜率,导数还表示函数在该点的变化率。
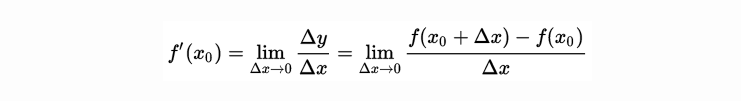
直白的来说,导数代表了在自变量变化趋于无穷小的时候,函数值的变化与自变量变化的比值代表了导数,几何意义有该点的切线。物理意义有该时刻的(瞬时)变化率...
注意在一元函数中,只有一个自变量变动,也就是说只存在一个方向的变化率,这也就是为什么一元函数没有偏导数的原因。
1、偏导数:多元函数在某个点他有多个偏导数(有多少个元就有多少个偏导数),比如二元函数一个是关于x一个是关于y&
版权声明:本文为m0_37957160原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。