描述

Levenshtein 距离，又称编辑距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离的算法是首先由俄国科学家 Levenshtein 提出的，故又叫 Levenshtein Distance 。

例如：

字符串A: abcdefg

字符串B: abcdef

通过增加或是删掉字符 ”g” 的方式达到目的。这两种方案都需要一次操作。把这个操作所需要的次数定义为两个字符串的距离。

要求：

给定任意两个字符串，写出一个算法计算它们的编辑距离。

数据范围：给定的字符串长度满足 1≤len(str)≤1000 

输入描述：

每组用例一共2行，为输入的两个字符串

输出描述：

每组用例输出一行，代表字符串的距离

示例1

输入：

abcdefg
abcdef

输出：

1

 解题思路

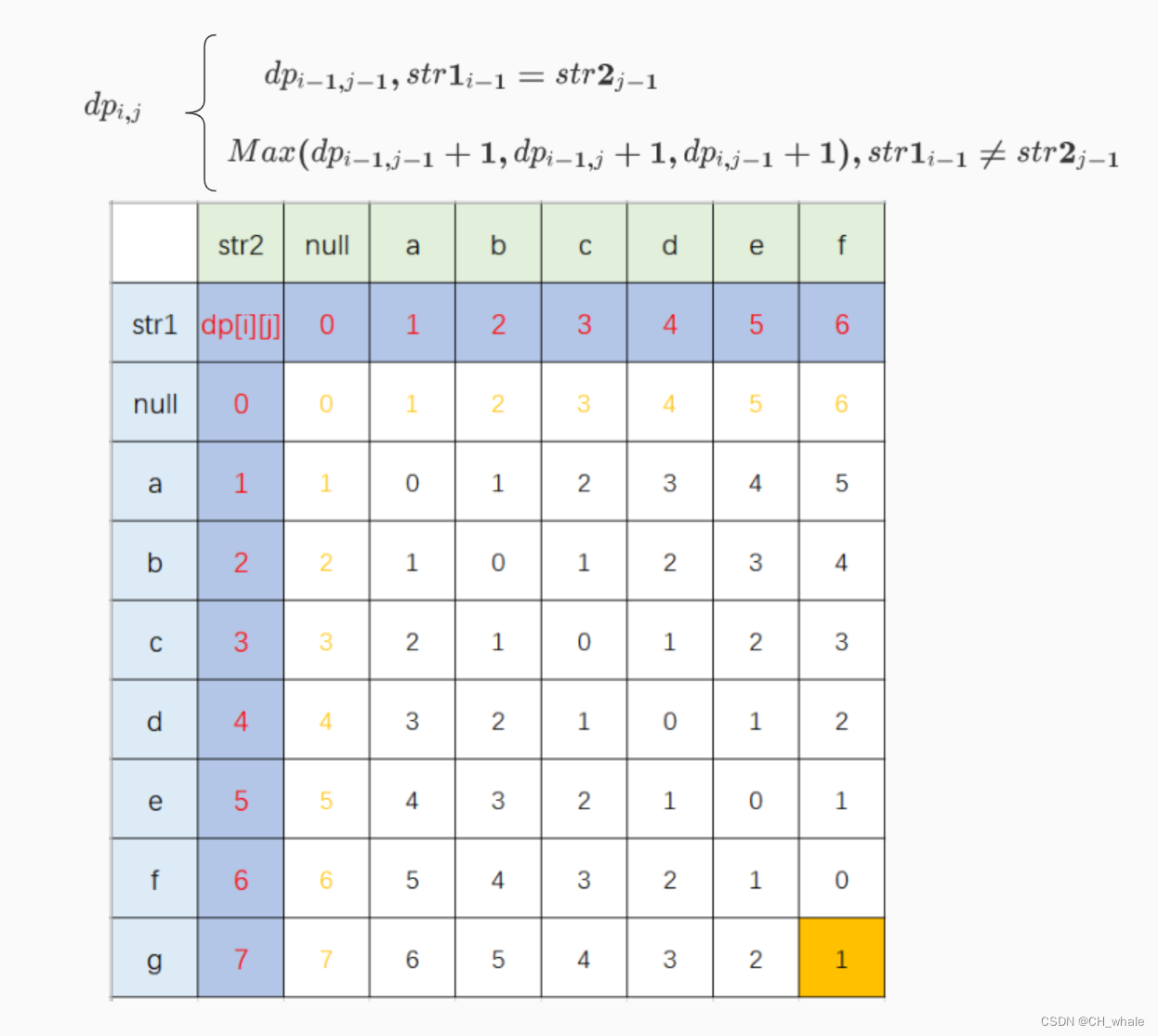
AC code

/// HJ52 计算字符串的编辑距离
#include <bits/stdc++.h>
using namespace std;

int main()
{
    string str1, str2;
    cin>>str1>>str2;

    int n = str1.size();
    int m = str2.size();

    int dp[n+1][m+1];

    // 边界初始化
    for(int i=0; i<=n; i++)
        dp[i][0] = i;
    for(int j=0; j<=m; j++)
        dp[0][j] = j;

    // 计算dp值
    int top=0, left=0, top_left=0;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
        {
            left = dp[i][j-1]+1;
            top = dp[i-1][j]+1;
            top_left = dp[i-1][j-1];
            if(str1[i-1]!=str2[j-1])
                top_left++;
            dp[i][j] = min(top, min(left, top_left));
        }

    cout<<dp[n][m]<<endl;

    return 0;
}