数据结构-邻接表Dijkstra算法求最短路径

C 语言实现邻接表Dijkstra算法求最短路径：

#include<stdio.h>
#include<stdlib.h>
#define MAXLEN 20  
#define INFINE 99999  

typedef struct ArcNode //定义结构体
{
	int adjvex;//邻接顶点下标
	int weight;//边的权值
	struct ArcNode *next; //指向下一个邻边节点指针
}ArcNode;

typedef struct
{
	char vertex;//顶点标志
	ArcNode *firstedge;//保存第一个边节点指针

}VertexNode;

typedef struct
{
	VertexNode adjlist[MAXLEN];//顶点数组
	int vexnum;  //顶点数　
	int arcnum;  //边数
}AdjList;

//创建邻接表
AdjList *Created_Graph(AdjList *G)
{
	int i, k, weight;
	ArcNode *s;
	char vex1, vex2; //顶点标志
	int n1, n2;//顶点下标
	printf("请输入顶点数和边数(输入格式为:顶点数,边数)：\n");
	scanf_s("%d,%d", &G->vexnum, &G->arcnum);
	printf("请输入顶点信息:\n");
	for (i = 1; i <= G->vexnum; i++)
	{
		printf("No.%d号顶点的信息:", i);
		scanf_s(" %c", &G->adjlist[i].vertex,1);
		G->adjlist[i].firstedge = NULL;   //头节点指向为空;
	}
	printf("请输入边的信息(输入格式为:V1,V2)：\n");
	for (k = 1; k <= G->arcnum; k++) {
		printf("请输入第%d条边:", k);
		scanf_s(" %c, %c", &vex1, 1, &vex2, 1);//多传参数"1",解决两个连续%c%c输入问题
		for (i = 1; i <= G->vexnum; i++) {
			if (G->adjlist[i].vertex == vex1) { n1 = i; }
			if (G->adjlist[i].vertex == vex2) { n2 = i; }
		}
		printf("请输入边权值:");
		scanf_s("%d", &weight);
		s = (ArcNode *)malloc(sizeof(ArcNode));
		s->adjvex = n2;
		s->weight = weight;
		s->next = G->adjlist[n1].firstedge;
		G->adjlist[n1].firstedge = s;
	}
	return G;

}

//获取位置
int getPosition(AdjList *G, char c)
{
	int m;
	for (m = 1; m <= G->vexnum; m++) {
		if (G->adjlist[m].vertex == c) {
			return  m;
		}
	}
	return 1;
}

//获取G中边<start, end>的权值；若start和end不是连通的，则返回无穷大。
int get_weight(AdjList *G, int start, int end)
{
	ArcNode *node;

	if (start == end)
		return 0;

	node = G->adjlist[start].firstedge;
	while (node != NULL)
	{
		if (end == node->adjvex)
			return node->weight;
		node = node->next;
	}

	return INFINE;
}

/*
* 迪杰斯特拉算法求最短路径。统计图(G)中"顶点vs"到其它各个顶点的最短路径。
* 参数说明：
* G -- 邻接图
* vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
* prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
* dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
*/
void Dijkstra(AdjList *G, int vs, int prev[], int dist[])
{
	int i, j, k, t,m;
	int min;
	int tmp;
	int flag[INFINE];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
	int path[MAXLEN][MAXLEN]={0};
	// 初始化
	for (i = 1; i <= G->vexnum; i++)
	{
		flag[i] = 0;                     // 顶点i的最短路径还没获取到。
		prev[i] = 0;                     // 顶点i的前驱顶点为0。
		dist[i] = get_weight(G, vs, i);  // 顶点i的最短路径为"顶点vs"到"顶点i"的权。
		path[i][0] = 0;
	}
	// 对"顶点vs"自身进行初始化
	flag[vs] = 1;
	dist[vs] = 0;
	path[vs][0] =1;
	// 遍历G->vexnum-1次；每次找出一个顶点的最短路径。
	for (i = 2; i <= G->vexnum; i++)
	{

		// 寻找当前最小的路径，即在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
		t = 0;
		min = INFINE;
		for (j = 1; j <= G->vexnum; j++)
		{
			if (flag[j] == 0 && dist[j]<min)
			{
				//G->adjlist[j].vertex;
				min = dist[j];
				k = j;
				
			}
		}

		// 标记"顶点k"为已经获取到最短路径
		flag[k] = 1;
		// 修正当前最短路径和前驱顶点，即当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
		for (j = 1; j <= G->vexnum; j++)
		{
			tmp = get_weight(G, k, j);
			tmp = (tmp == INFINE ? INFINE : (min + tmp)); // 防止溢出
			if (flag[j] == 0 && (tmp  < dist[j]))
			{
				dist[j] = tmp;
				prev[j] = k;
				path[j][t] = k;
				t++;
			}
		}
	}

	// 打印dijkstra最短路径的结果
	printf("当前起点(%c)到各个顶点的最短距离如下所示: \n", G->adjlist[vs].vertex);
	for (i = 1; i <= G->vexnum; i++)
	{
		int showpath[MAXLEN] = {0};//存储最短路径上的节点
		for (m = 0; m < G->vexnum; m++)
		{
			if (path[i][m] == 0|| G->adjlist[path[i][m]].vertex == G->adjlist[vs].vertex) {
				break;
			}
			showpath[m] = path[i][m];
		}
		printf("最短路径长度(%c, %c)=%d", G->adjlist[vs].vertex, G->adjlist[i].vertex, dist[i]);
		//以下用于拼接路径
		if (dist[i]!= INFINE)
		{
			printf("\t当前最短路径为%c->", G->adjlist[vs].vertex);
			for (int q = MAXLEN - 1; q >= 0; q--)//存入的中间节点是【距离原点最远的顶点】依次递减存入的，故需逆序输出
			{
				if (showpath[q] == 0) { continue; }
				printf("%c->", G->adjlist[showpath[q]].vertex);
			}
			printf("%c\n", G->adjlist[i].vertex);
		}
		else
		{
			printf("当前路径不连通,无最短路径\n");
		}
		
	}
	

}



int main()
{
	AdjList G;
	char start1;
	int ps;
	int dist[MAXLEN], prev[MAXLEN];
	AdjList *G2 = Created_Graph(&G);//创建表
	printf("请输入起点信息:");
	scanf_s(" %c", &start1,1);
	ps = getPosition(G2, start1);//获取起点位置
	Dijkstra(G2, ps, prev, dist);
	system("pause");
	return 0;

}

需要操作的邻接表实例：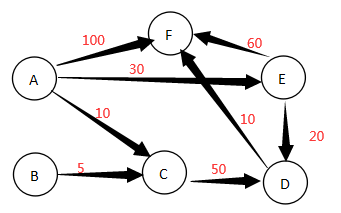

操作结果：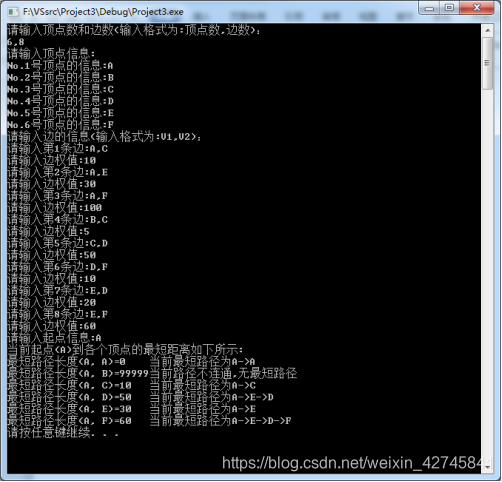

参考地址：https://github.com/wangkuiwu/datastructs_and_algorithm/blob/master/source/graph/dijkstra/udg/c/list_udg.c