拉普拉斯算子属于卷积方法吗_公式墙(1)——Laplace Transform(拉普拉斯变换)

致敬Laplace！

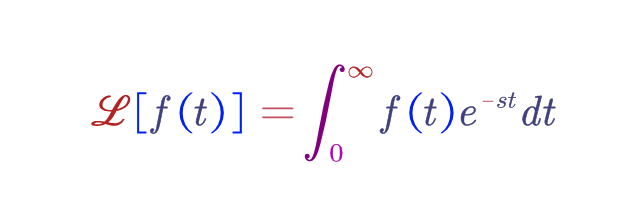
如果喜欢文章，请收藏时点一个赞以便其他朋友能看到

前两天在外没有书，正巧要用一些拉普拉斯变换的知识点，知乎很多大佬关于拉氏变换写的非常详细，可以说非常完美，但我找公式也确实找了很久，于是我就决定，自己写一篇关于LT的文章，准备略写一些理解，主要以公式为主，而且以后我写文章可能比较倾向于这种了，因为那些逻辑清晰的文章我也不会写(悲)，毕竟我写文章有一部分初衷也是方便大家拿来用，所以说决定做一个长期系列——“公式墙”系列文章。

如果要谈这篇文章的话，可能有朋友要问，为什么不讲FT再讲LT呢？我一开始也决定先写一下傅氏变换再写拉氏变换，但一方面时间少，写不完，另一方面，看了就知道了......所以就跳过FT吧/逃

※目录 Part 1 . Laplace变换概念 Part 2 . Laplace变换相关公式 Part 3 . Laplace变换公式部分推导 Part 4 . Laplace变换公式应用

·Part 1 . Laplace变换概念

话不多说，上定义式！

其中，
是Laplace变换算子，
或者
都可以，（知乎只支持这个，其实这个在latex语言中不算拉普拉斯算子)
，且
为实数，
是虚数单位，即

顺便把傅里叶变换搬出来

(不同文献表示方法不同)

然后会发现，不看上下限的话(可以参考双边Laplace变换)，其实总的来说，拉氏变换就是多一个

(称之为衰减因子)，因此，某些时候，拉氏变换适用的，傅氏变换也适用。

另外，为了方便叙述，
称之为频域，
称之为时域
，
是
衰减因子的指数
其中，
叫做
的
像函数，
叫做
的
原函数

此外还有一个叫做“拉普拉斯逆变换”

其中
是一个使
的积分路径在收敛域内的实数

·Part 2 . Laplace变换相关公式

同理，话不多说，直接上公式/笑

对于函数
满足下面两个条件：
在
的任何
有限区间上 分段连续；
在
时，存在常数
和
使得

所谓存在，也就是

在

一定存在且解析

. 线性叠加性

直接由积分算子的线性性质得到， 证明略

. 微分性质

证明附后

. 积分性质

证明附后

照此易得
易证，留做习题

. 平移延迟

(ps:其中,
为阶跃函数，在信号与系统中常常为
经常亦写作
或
之类)
证明附后

算作推论，证明从略

. 卷积定理

卷积定义:
，当
时
(其实这种情况很常见)，则显然

卷积定理
证明附后

Part 3 . Laplace变换公式部分推导

为了一定的严谨性，这里规定以下所有函数均存在拉普拉斯变换上面公式确实没用想象的那么多，因为我对物理方面的运用知之甚少，只能玩玩数学上的运用，包括Part 4 要讲的东西也都会是数学运用，至于物理学运用可以去看《信号与系统》

pf：我们用定义式展开，得到
，

然后分部积分，
得到
，

由于存在性原理，显然可得

因此

往死里迭代，即可得到
证毕

pf：我们利用上面结论

做换元，
,
显然,
,

套进得到

即

pf：直接Laplace得到

做换元
，立刻证到：

抄下来

套入卷积定义式

显然要用换元
，立马

抄下来

Part 4 . Laplace变换公式应用

以上内容就是一些公式，下面我们举几个常见例子练练手

先来几个常用的拉普拉斯变换吧

计算Dirichlet积分

sol——
先 let

利用
公式，得到

然后等式左边

得到

令
，

计算Laplace积分

sol——
注意到
，我们不对
变换，对
！

直接求

(看不懂第一个等号后面的点我)
于是

这个积分挺有趣的，我一开始以为不能求不定积分，就用了复变大法

想来想去，与其这样不如：
那拉普拉斯变换不就多余了吗！
早上上学跑操的时候灵光一现(以后得多跑操/smile)

我们带入上下限
wuwuwu! 注意到
，则

抄下来

如果想学更多关于Laplace 物理的运用和数学实例，极力推荐大佬 @TravorLZH 的文章：

TravorLZH：拉普拉斯变换的那些事儿——定义、性质与Airy常微分方程zhuanlan.zhihu.com

·后记

时间紧迫，还有好多有趣的积分想分享，估计是没时间了，待我中考过后，保证补上(哭)

只有写文章之后才会发现自己latex多么辣鸡，这篇文章我每天晚上写一个小时，写了三个小时(啊哈哈哈，别笑我)

......

(未完待续——将于7月20左右更新)

never end