一【题目类别】

• 位运算

二【题目难度】

• 简单

三【题目编号】

• 231.2的幂

四【题目描述】

• 给你一个整数 $n$，请你判断该整数是否是 $2$ 的幂次方。如果是，返回 $true$ ；否则，返回 $false$ 。
• 如果存在一个整数 $x$ 使得 $n==2^x$ ，则认为 $n$ 是 $2$ 的幂次方。

五【题目示例】

• 示例 1：

  • 输入：n = 1
  • 输出：true
  • 解释：20 = 1

• 示例 2：

  • 输入：n = 16
  • 输出：true
  • 解释：24 = 16

• 示例 3：

  • 输入：n = 3
  • 输出：false

• 示例 4：

  • 输入：n = 4
  • 输出：true

• 示例 5：

  • 输入：n = 5
  • 输出：false

六【解题思路】

• 本体使用位运算的思想
• 对于某个2的幂的数字n，其二进制只有一个1，也就是类似于a1000……的形式，其中a代表全为0
• 对于某个2的幂的小一位的数字n-1，其二进制有n-1个1，也就是类似于a0111……的形式，其中a代表全为0
• 我们令n & (n - 1)，如果其结果为0，说明数字n就是2的幂，否则就不是2的幂，因为如果不是2的幂，其二进制类似于a1000……的形式，不过其中的a不全为0，也就导致了最后的结果不是0，而如果数字n是2的幂，其二进制中的a全为0，最后的结果也就是0，以此为判断依据就可以得到结果
• 还需要注意，2的幂的数字n肯定大于0，所以对于小于或者等于0的数字肯定不是2的幂
• 最后返回结果即可

七【题目提示】

• $-2^{31}<=n<=2^{31}-1$

八【题目进阶】

• 你能够不使用循环/递归解决此问题吗？

九【时间频度】

• 时间复杂度：$O(1)$
• 空间复杂度：$O(1)$

十【代码实现】

1. Java语言版

class Solution {
    public boolean isPowerOfTwo(int n) {
        return n > 0 && (n & (n - 1)) == 0;
    }
}

2. C语言版

bool isPowerOfTwo(int n)
{
    return n > 0 && (n & (n - 1)) == 0;
}

3. Python语言版

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        return n > 0 and (n & (n - 1)) == 0

4. C++语言版

class Solution {
public:
    bool isPowerOfTwo(int n) {
        return n > 0 && (n & (n - 1)) == 0;
    }
};

十一【提交结果】

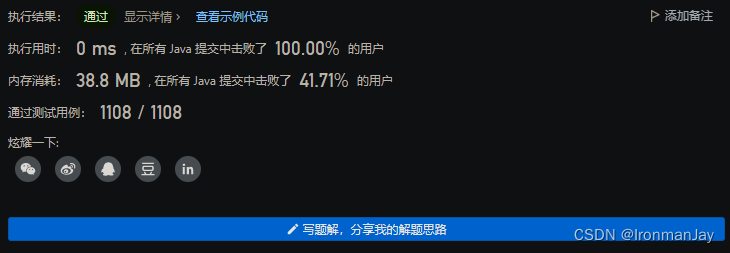
1. Java语言版
   

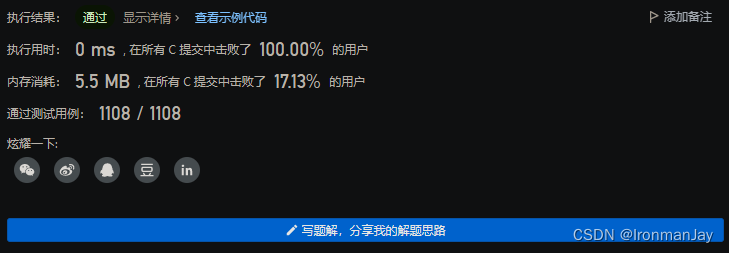
2. C语言版
   

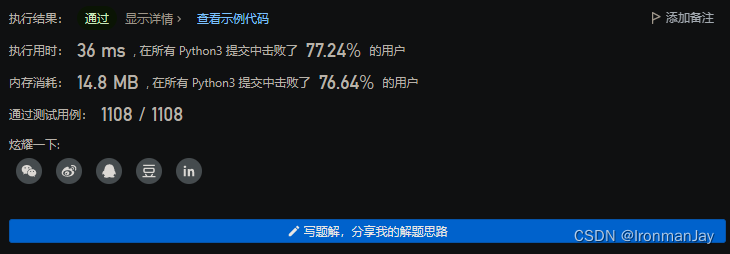
3. Python语言版
   

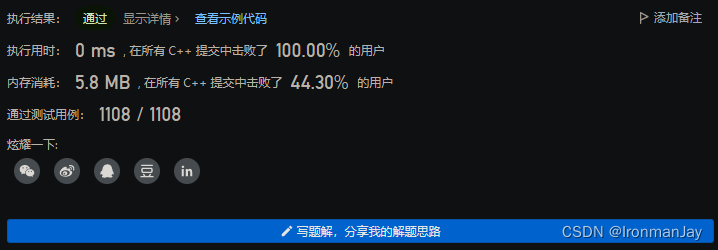
4. C++语言版