什么是偏度和峰度?
前言
在本文中,我们将介绍描述性统计中的两个重要概念-偏度和峰度。 在本文的结尾,您将获得以下问题的答案,例如:
什么是偏度和峰度?
右/左偏度?
如何测量偏度和峰度,如何使用等等。
偏度(Skewness)
意义:
偏度是对实值随机变量的概率分布的不对称性的度量
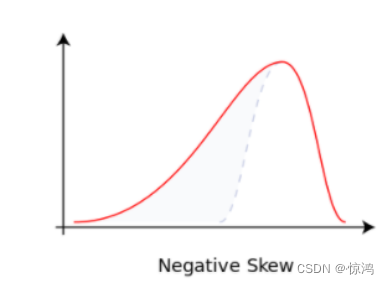
负偏度(Negative Skewness)
数据比较集中在右侧,如下图所示,因此,左侧有一条长长的尾巴,也成为 左尾或左偏
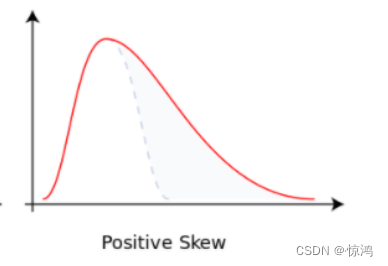
正偏度(Positive Skewness)
数据比较集中在左侧,如下所示,因此,右侧有一条长长的尾巴,也称为 右尾或右偏
如何解释偏度
经验法则说:
- 如果偏度在 -0.5 到 0.5之间,那么数据是相当对称的,也就是 正态分布
- 如果偏度在 -1 到 -0.5(负偏度)或者 0.5 - 1(正偏度)之间,则 数据倾斜
- 如果偏度在 小于 -1(负偏度)后者 大于 1(正偏度)之间, 则 数据高度倾斜
- 正态分布:众数 = 中位数 = 均值
- 右偏:众数 < 中位数 < 均值
- 左偏:均值 < 中位数 < 众数
如果数据符合正态分布,那么他的偏度将为0,但是 在现实世界中,我们找不到完全符合正态分布的数,因此,对于任何现实世界中的数数据,我们都找不到精确的0偏度,但是它 可以接近0
为什么要研究偏度?
考虑下面的例子。 这里total_bill正偏,数据点集中在左侧。 如果我们要以此为基础构建模型,则与更高的total_bill相比, total_bill较低的模型将做出更好的预测。
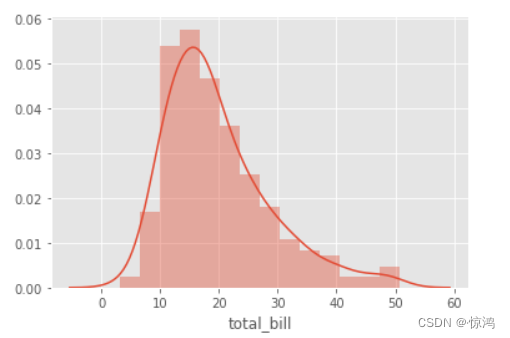
偏度告诉我们异常值的方向。 从上面的分布中,我们可以清楚地说出异常值出现在分布的右侧。
如何处理偏斜的数据
许多统计测试和机器学习模型都依赖于正态性假设。 因此,严重偏斜意味着数据不正常,并且可能会影响您的统计测试或机器学习预测能力。 在这种情况下,我们需要转换数据以使其正常。 用于处理偏斜数据的一些常用技术:
- Log transformation
日志转换 - Square root transformation
平方根变换 - Power transformation
动力转换 - Exponential transformation
指数变换 - Box-Cox transformation, etc
Box-Cox转换等
峰度(Kurtosis)
峰度是对实值随机变量的概率分布的“尾部”度量
通常用于表示给定数据中的异常值,比如极值
由于是用于识别离群值,因此使用尾部的极值来进行分析
峰度的类型以及如何解释
- Mesokurtic(峰度= 3) :此分布显示峰度3 接近0,极值(离群值)的分布与正态分布相似
- Leptokurtic (Kurtosis > 3) :这种分布比 等于3有更大的峰度,该峰比中胚层更高更尖锐,他的两边都有粗尾,表示离群值较大, 在投资世界中,Leptokurtic发行意味着它是高风险的投资。
- Platykurtic: (Kurtosis < 3) :此分布显示峰度比中胚偏低,该峰比中胚层低且厚。他的两次显示平坦的尾巴,表示离群值较小,在投资世界中,platykurtic发行意味着它是一种低风险的投资。
如图: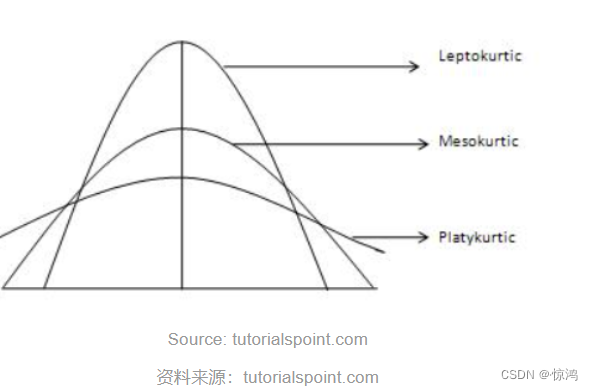
版权声明:本文为qq_40608132原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。