欧拉函数相关概念

一、欧拉函数

• 给定正整数n，欧拉函数φ(n)=不大于n且和n互质的正整数的个数(包括1)。
• φ(1)=1
• $\phi \left(n\right)={\Sigma }_{i=1}^n\left[gcd\left(i,n\right)==1\right]$

完全余数集合: Zn={ 不大于n 且和n 互质的数} |Zn| ＝φ(n)

性质

(1)p为素数 ，则 φ( p)=p -1

质数与小于它的每一个，都构成互关系。 质数与小于它的每一个，都构成互关系。

(2)p为素数，正整数 $n=p^k$，则 $\phi \left(n\right)=p^k-p^{k-1}$ 或者写作 $\phi \left(n\right)=p^{k-1}\left(p-1\right)=p^k\left(1-\frac{1}{p}\right)$

证明：

小于 $p^k$ 的正整数个数为$p^k-1$个，其中与$p^k$不互质的正整数有{p,2p,3p,4p,…,$(p^{k-1}-1)p$},共计$p^{k-1}-1$个

所以 $\phi \left(n\right)=p^k-1-\left(p^{k-1}-1\right)=p^k-p^{k-1}$

（3）两个素数 p,q ,n=p * q​，则 φ(n) =( p-1) * ( q-1)

证明：

Zn={1,2,3,…,n-1}-{p,2p,3p,…,(q-1)p}-{q,2q,3q,…,(p-1)q}

φ(n)=(n-1)-(q-1)-(p-1)
=(p * q-1)-(p-1)-(q-1)
=(p * q-p)-(q-1)
=p(q-1)-(q-1)
=(p-1)(q-1)

(4)当b时质数,a%b=0,则φ(ab)=φ(a)b

证明：

设 $a=k{b}^n$ 且gcd(k,b)=1，则 $\phi (a)=\phi (k)\phi (b^n)$，$\phi (k)=\frac{\phi (a)}{\phi (b^n)}$

$\phi (ab)=\phi (k{b}^{n+1})=\phi (k)\phi (b^{n+1})=\frac{\phi (a)}{\phi (b^n)}\phi (b^{n+1})=\phi (a)(\frac{\phi (b^{n+1})}{\phi (b^n)})=\phi (a)b$

$\phi (b^{n+!})=b^{n+1}-b^n,\phi (b^n)=b^n-b^{n-1}$

(5)任意正整数n： $n=p_1^{a_1}{p}_2^{a_2}...p_m^{a_m}$ ( $p_i$ 为素数)，$\phi (n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_m})$

证明：

$\phi (n)=\phi (p_1^{a_1})\phi (p_2^{a_2})...\phi (p_m^{a_m})$

$=(p_1^{a_1}{p}_2^{a_2}...p_m^{a_m})(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_m})$ (由性质(2)知）

$=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_m})$ (被称为欧拉函数计算公式)

如何进一步理解欧拉函数计算公式？

(6)欧拉函数递推式：可用于线性求1~n所有数的欧拉函数

给定质数p，满足p|x,

若p²|x不成立，则$\phi (x)=\phi (\frac{x}{p})\ast (p-1)$

若p²|x成立，则$\phi (x)=\phi (\frac{x}{p})\ast p$

欧拉函数打表：

int primes[N], euler[N], cnt;
bool st[N];
void get_eulers(int n)
{
	euler[1] = 1;
	for (int i=2; i <= n; i++ ){
		if ( !st[i] ){
		primes[cnt++] = i;
		euler[i] = i-1;
		}
		for ( int j=0; primes[ j] <= n/i; j++ ){
		st[ primes[ j]*i ] = true;
        
			if ( i % primes[ j] == 0 ) {
				euler[ i*primes[ j] ] = euler[i] * primes[ j];
				break;
				}
		euler[ i*primes[ j] ] = euler[i] * ( primes[j]-1 );
		}
	}
}

(7)整数n 等于n的所有约数(包括1和n)的欧拉函数之和，即$n={\Sigma }_{d|n}\phi \left(d\right)$

(8)给定整数n，所有小于n且与n互质的数的和是$n\ast \frac{\phi (n)}{2}$

1. 小于n的与n互质数i 和n-i 总是成对出现，且它们的和是n；

   小于n的且与n互质 数的个数是φ(n)。

2. 所以，${\Sigma }_{i=1}^{n-1}i\left[gcd\left(i,n\right)==1\right]=n\ast \phi \left(n\right)/2$，还需分析i=n-i的情况 (即n为偶数情况)

   (1)如果n是奇数，i≠n-i

   (2)如果n是大于2的偶数，gcd(n,n/2)≠1

   (3)如果n是2，$n\ast \frac{\phi (n)}{2}=2\ast \frac{1}{2}=1$

性质：若 gcd(n,i)=1，则 gcd(n,n-i)=1(1≤i≤n)

反证法：

如果存在k≠1 使gcd(n,n-i)=k，那么(n-i)%k=0，n%k=0，n=k * j

→ (k * j-i)%k=0 → k * j%k-i%k=0 → i%k=0

因为k是n的因子， i%k=0 → gcd(n,i)=k，与原命题矛盾。

二、欧拉定理

1.欧拉定理

正整数a和n互质，有$a^{\phi (n)}\equiv 1modn$

证明：

1.令Zn={ $x_1,x_2,...,x_{\phi (n)}$ }为 φ(n)个<n且与n互质的数 $x_i$ ,

构造S={ $a{x}_1$%n , $a{x}_2$%2 , …$a{x}_{\phi (n)}$%n}

即要证：Zn=S

（1）a与n互质 且 $x_i$与n互质 → $a{x}_i$ 与n互质 → $a{x}_{i}modn\in Zn$

（2）若i≠j，则 $x_i\ne x_j$ → $a{x}_i$%n ≠ $a{x}_j$%n (否则由模运算消去律，$x_i=x_j$)

2.证： $a^{\phi (n)}{x}_1{x}_2...x_{\phi (n)}modn\equiv (a{x}_1)(a{x}_2)...(a{x}_{\phi (n)}modn)$

​ $\equiv (a{x}_{1}modn)(a{x}_{2}modn)...(a{x}_{\phi (n)}modn)\equiv x_1{x}_2...x_{\phi (n)}modn$

所以有：$a^{\phi (n)}{x}_1{x}_2...x_{\phi (n)}\equiv x_1{x}_2...x_{\phi (n)}modn$

因为 $x_i$ （1≤i≤φ(n) ）与n互质，所以 $a^{\phi (n)}\equiv 1modn$ （消去律）

模运算消去律：若gcd(c,p)=1,则ac≡bc mod p → a≡b mod p

证明：

ac ≡ bc mod p → c(a -b) = kp

gcd (c,p )=1 → 存在 2种可能： 1) c 能整除 k 2)a=b

如果 2) 成立，命题 a ≡ b mod p 显然成立

如果 1) 成立 ，则 k = ck‘

→ c(a -b)= kp 可改写为 c(a -b) = ck‘p

所以 a-b= k‘p,得出 a ≡ b mod p

2.费马小定理

若正整数a与素数p互质，则有$a^{p-1}\equiv 1(modp)$,或写为$a^p\equiv a(modp)$

φ§=p-1

费马小定理求逆元

若p为素数，$a^{p-1}\equiv 1(modp)$ → $a{a}^{p-2}\equiv 1(modp)$

欧拉定理求逆元

若a,p互素，$a^{\phi (p)}\equiv 1(modp)$ → $a{a}^{\phi (p)-1}\equiv 1(modp)$

3.整数的阶

设a与n是互质的正整数，使得 $a^x\equiv 1$ mod n 成立的最小正整数x 称为整数a模n的阶，记为 $or{d}_{n}a$

4.原根

设a与n是互质的正整数且n>0，则当 $or{d}_{n}a|\phi (n)$ 时，称a为模n的原根，即a满足$a^{\phi (n)}\equiv 1modn$

特点：

1. 所有的素数p一定有原根，且模p的原根个数为φ(p-1)。

2. 不是所有的整数都有原根。

原根存在的条件

模m有原根的充要条件：m=2, 4, $p^t$, $2\cdot p^t$ ，其中p为奇质数，t为正整数

性质

1. 设a与m是互质的正整数且m>0，则如果a是模m的一个原根，那么整数a, $a^2$ , … , $a^{\phi (m)}$ 构成模m的简化剩余系。

2. 设g 是模m的一个原根，i 是一个正整数，那么 $g^i$ 也是模m的原根的充要条件是gcd(i,φ(m))=1 。

​ $or{d}_m(au)$ 的性质：若u是一个正整数，且 $or{d}_{m}a=t$ ,则 $or{d}_m(a^u)=\frac{t}{gcd(t,u)}$

​ 推论：当正整数m 有原根时，则有φ(φ(m)) 个原根。

3. 一个数的最小原根的不超过$m^{\frac{1}{4}}$

求最小原根：依次枚举2~ $m^{\frac{1}{4}}$ 判断即可

求所有原根：枚举最小原根的指数即可

5.计算大数取模

求 (a^b)%m 的值，其中a,b都可能很大

快速幂求 (a^b)%m

• (a^b)%m =(a%m)^b)%m

• 用带模快速幂计算，时间复杂度O(log b)；但当b是超大数时，我们还需要更快的算法。

三、欧拉降幂

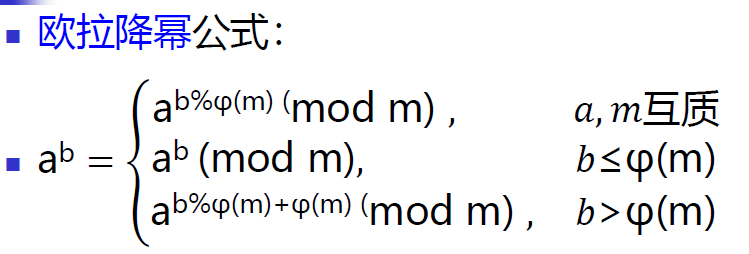
四、习题

Euler Function HDU-6322

Farey Sequence POJ-2478

LCM SUM SPOJ-5971

Longge的问题 BZOJ-2705

Count a × b HDU-5528

The Luckiest number POJ-3696

Period of Inf. Bin. Exp. POJ-3358

Sum HDU-4704

A ternary string 2018牛客暑期训练营

Xyjj’s sequence 2019ICPC南昌邀请赛

Visible Lattice Points POJ-3090 (欧拉函数)

Stern-Brocot Tree HDU-4556 (法里数列)

沙拉公主的困惑 SDOI2008 (欧拉函数+模逆)

欧拉心算 BZOJ-4804 (欧拉函数)

Bi-shoe and Phi-shoe LightOJ-1370 (欧拉函数)

BZOJ-4173 (欧拉函数)

Description has only two Sentences HDU-3307 (欧拉定理)

上帝与集合的正确用法 BZOJ-3884 (欧拉降幂)

Brute-force Algorithm HDU-3221 (欧拉降幂+矩阵快速幂)

子序列 (欧拉降幂)

五、相关链接

原根