拉普拉斯变换公式表_假期搞积——拉普拉斯积分的随想

---

---

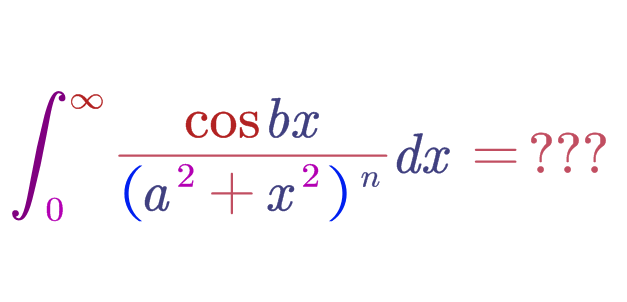
我们都知道这么一个可爱的积分

既然是拉普拉斯积分，那当然可以用拉普拉斯发明的工具——拉普拉斯变换来搞呗

至于求解过程，参考以下文章：

弧长长长长长：公式墙(1)——Laplace Transform(拉普拉斯变换)​zhuanlan.zhihu.com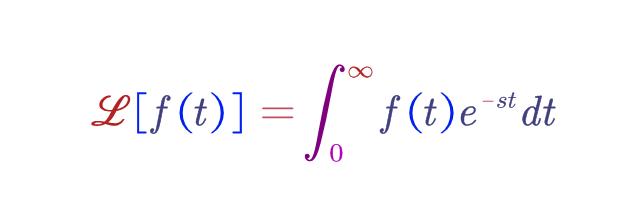

---

我们稍加变换，变成另一个积分：

我们这次不用拉普拉斯变换，咱用微分方程淦它~

我们先把

(后面会体现出这一点)：

于是就很容易发现

沿用拉普拉斯积分计算方法，考虑到在三阶导形式变形

很容易发现

这个太太太好解了，为了详略得当，解略

具体解法可参照大佬 @Aries 的文章

Aries：初三党搞积日常（1）​zhuanlan.zhihu.com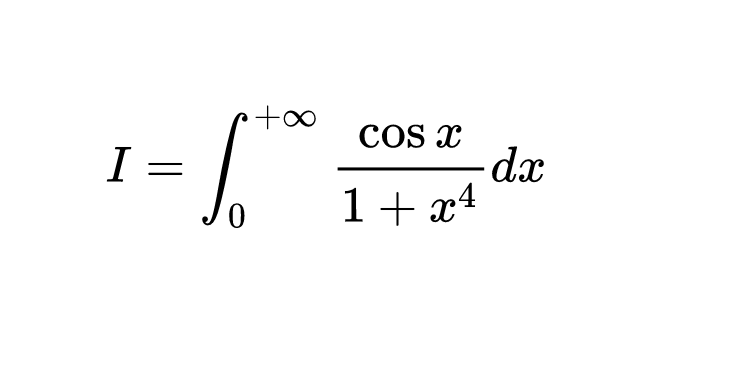

---

---

看完这个，我们不妨再思考思考，我再把分母变一下

这玩意儿可咋整啊

算了，直接无脑留数定理，

构造半圆围道

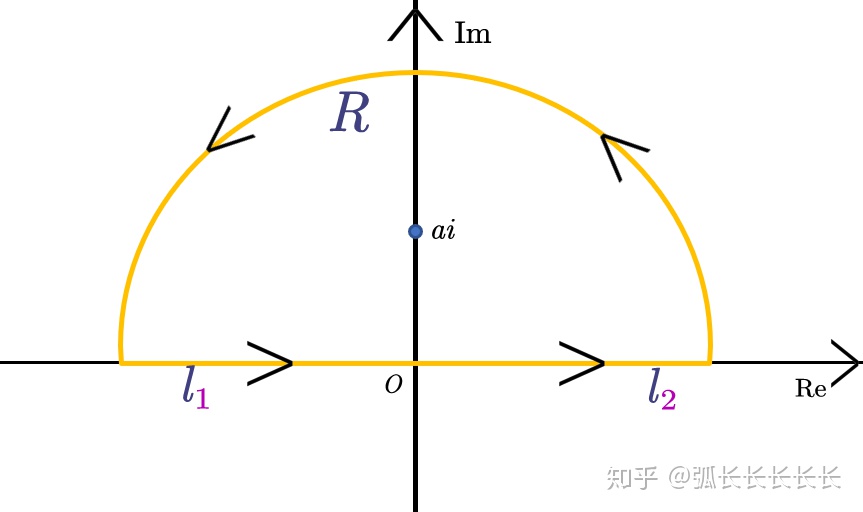
由留数定理

由

下面来计算留数，让我们打开MMA......(好吧不闹了)

SO：

Finally:

呼，过了~

(那个留数真的把我差点算死了~[求导不过关])

---

别急，现在才进入正题！我们思考一下封面上的积分

别的骚办法我也不思考了，咱们还是用留数定理

而且

明显需要利用 leibniz 求导法则

由递推可得

带入即得到

When

When

带到Leibniz公式

SO~

Finally：

上帝保佑我没算错~

---

这一期文章比较爽，但是就是有点费手~

留几个习题

---

---