lightGBM----学习笔记整理

1、前序

1.1、lightGBM演进过程

c3.0(信息增益，信息增益率)—> CART(Gini) —> 提升树（AdaBoost) —> GBDT —> XGBoost —> lightGBM

1.2、AdaBoost算法

AdaBoost是一种提升树的方法，和三个臭皮匠，赛过诸葛亮的道理一样。

AdaBoost两个问题

1、如何改变训练数据的权重或概率分布

提高前一轮被弱分类器错误分类的样本权重，降低前一轮被分对的权重

2、如何将弱分类器组合成一个强分类器，亦即，每个分类器，前面如何设置

采取多数表决的方法，加大分类错误率小的弱分类器权重，使其作用较大，而减少分类错误率大的弱分类器的权重使其在表决中起较小作用。

1.3、GBDT算法以及优缺点

GBDT和其它Boosting算法一样，通常将表现一般的几个模型（通常是深度固定的决策树）组合在一起来集成一个表现较好的模型

AdaBoost是通过提升错分数据点的权重来定位模型的不足。

缺点：1、空间消耗大 2、时间上也有较大开销 3、对内存优化不友好

2、lightGBM原理

2.1、优势

lightGBM主打的高效并行训练让其性能超越现有其它boosting工具。

速度惊人、支持分布式、代码清晰易懂、占用内存小

2.2、lightGBM原理

lightGBM主要基于以下方面优化，提升整体特性

1、基于Histogram（直方图）的决策树算法

2、lightGBM的Histogram（直方图）做差加速

3、带深度限制的leaf-wise的叶子生长策略

4、直接支持类别特征

5、直接支持高效并行

2.3、基于Histogram（直方图）的决策树算法

直方图算法的基本思想

先把连续的浮点特征值离散化成K个整数，同时构造一个宽度为k的直方图

在遍历数据的时候，根据离散化后的值作为索引在直方图中累计统计量，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。

如 [0,0.1]—>0 [0.1,0.3]—>1

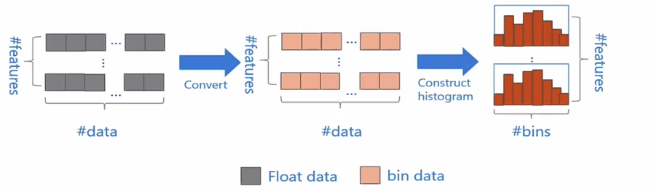
在这里插入图片描述

使用直方图算法有很多优点，首先最明显的就是内存消耗的降低，直方图算法不仅不需要额外存储预排序的结果，而且可以保存特征离散化后的值，而这个值一般用8位整型存储就够了，内存消耗降低为原来的1/8

在这里插入图片描述

然后在计算上的代价也是大幅降低。预排序算法每遍历一个特征就需要计算一次分裂的增益。而直方图算法只需要计算K次（k可认为是常数），时间复杂度从O（#data#feature）优化到O（k#feature)

Histogram算法并不是完美的，由于特征被离散化后，找到的并不是精确的分割点，所以对结果产生影响。但是在不同的数据集上的结果表明，离散化的分割点对最终精度影响并不是很大，甚至有时候会更好一点。原因是决策树本身就是弱模型，分割点是不是精确并不是太重要。较粗的分割点也有正则化的效果，可以有效防止过拟合。即使单棵树的训练误差比精确分割的算法稍大，但是梯度提升（Gradient Boosting)的框架下没有太大影响。

2.4、LightGBM的Histogram(直方图)做差加速

一个叶子的直方图可以由它的父亲节点的直方图与它兄弟节点的直方图做差得到。

在这里插入图片描述

2.5、带深度限制的Leaf-wise的叶子生长策略

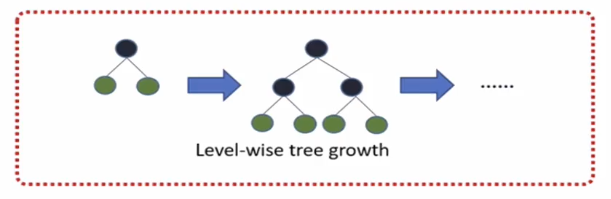
level-wise遍历一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。

但实际上Level-wise 是一种低效的算法，因为它不加区分的对待同一层叶子，带来了很多没必要的开销，因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂

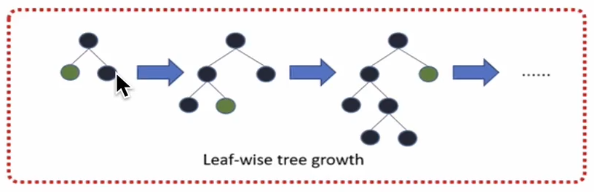
在这里插入图片描述

leaf-wise则是一种更为高效的策略，每次从当前所有叶子中，找到分裂增益最大的叶子，然后分裂，如此循环。

因此同leaf-wise相比，在分裂次数相同的情况下，leaf-wise可以降低更多的误差，得到更好的精度。

leaf-wise的缺点是可能会长成比较深的决策树，产生过拟合。因此LightGBM在leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。

在这里插入图片描述

2.6、直接支持类别特征

lightGBM是第一个直接支持类别特征的GBDT工具。

2.7、直接支持高效并行

3、lightGBM参数并行

3.1、control Parameters

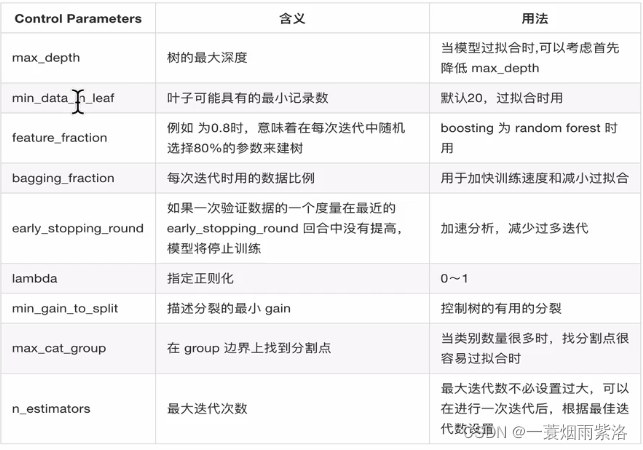
在这里插入图片描述

3.2、Core Parameters

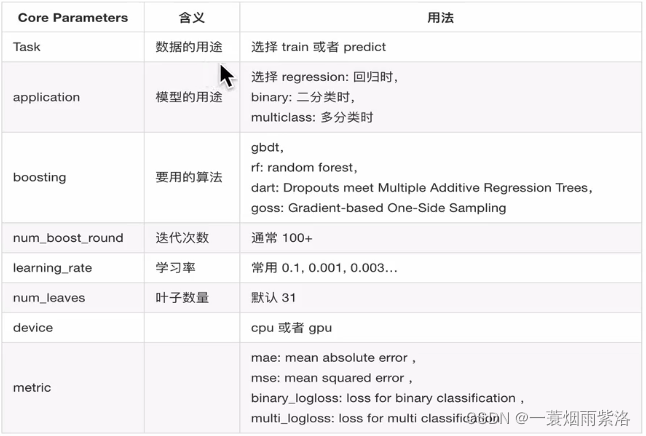
在这里插入图片描述

3.3、IO parameter

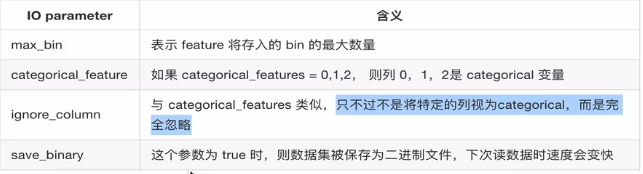
在这里插入图片描述

3.4、调参建议

在这里插入图片描述

4、鸢尾花数据对lightGBM的基本使用

from sklearn.datasets import load_iris
import seaborn as sns
import  matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection  import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error
import lightgbm as lgb

#1、数据获取
iris =load_iris()
data=iris.data
target=iris.target
data



#2、数据可视化
iris_d = pd.DataFrame(iris['data'],columns=['Sepal_Length','Sepal_Width','Petal_Length','Pepal_Width'])
iris_d['Species'] = iris.target


#3、数据集划分
x_train,x_test,y_train,y_test = train_test_split(data,target,test_size =0.2,random_state=22)
y_test.shape
y_train.shape

#4、模型基本训练
gbm =lgb.LGBMRegressor(objective="regression",learning_rate=0.05,n_estimators=200)
gbm.fit(x_train,y_train,eval_set=[(x_test,y_test)],eval_metric="11",early_stopping_rounds=3)
gbm.score(x_test,y_test)

#通过网格搜索进行训练
estimator=lgb.LGBMRegressor(num_leaves=31)
param_grid ={
    "learning_rate":[0.01,0.1,1],
    "n_estimators":[20,40,60,80]
}
gbm=GridSearchCV(estimator,param_grid,cv=5)
gbm.fit(x_train,y_train)

gbm.best_estimator_

gbm =lgb.LGBMRegressor(objective="regression",learning_rate=0.1,n_estimators=80)
gbm.fit(x_train,y_train,eval_set=[(x_test,y_test)],eval_metric="11",early_stopping_rounds=3)
gbm.score(x_test,y_test)

5、绝地求生玩家排名预测

5.1、项目背景

吃鸡

5.2、数据集介绍

数据来自所有类型比赛：单排、双排、四排。不保证每场比赛有100名人员，每组最多4名队员
预测哪一组可能是冠军

文件说明：

train_V2.csv --训练集

test_V2.csv—测试集

数据集中字段解释

Id	用户id	matchType	比赛类型（小组人数）
groupId	小组id	maxPlace	本局最差排名
matchId	比赛id	numGroups	小组数量
assists	助攻数	rankPoints	ELO排名
boosts	使用能量	revives	救活队员的次数
damageDealt	总伤害	rideDistance	驾车距离
DBNOs	击倒敌人数	roadKills	驾车杀敌数
headshotKills	爆头数	swimDistance	游泳距离
heals	使用治疗药品数量	teamKills	杀死队友的次数
killPlace	本场比赛杀敌排行	vehicleDestroys	毁坏机动车的数量
killPoints	Elo杀敌排名	walkDistance	步行距离
kills	杀敌数	weaponsAcquired	收藏武器的数量
killStreaks	连续杀敌数量	winPoints	胜率Elo排名
longestKill	最远杀敌距离	winpalcePerc	百分比排名

数据集

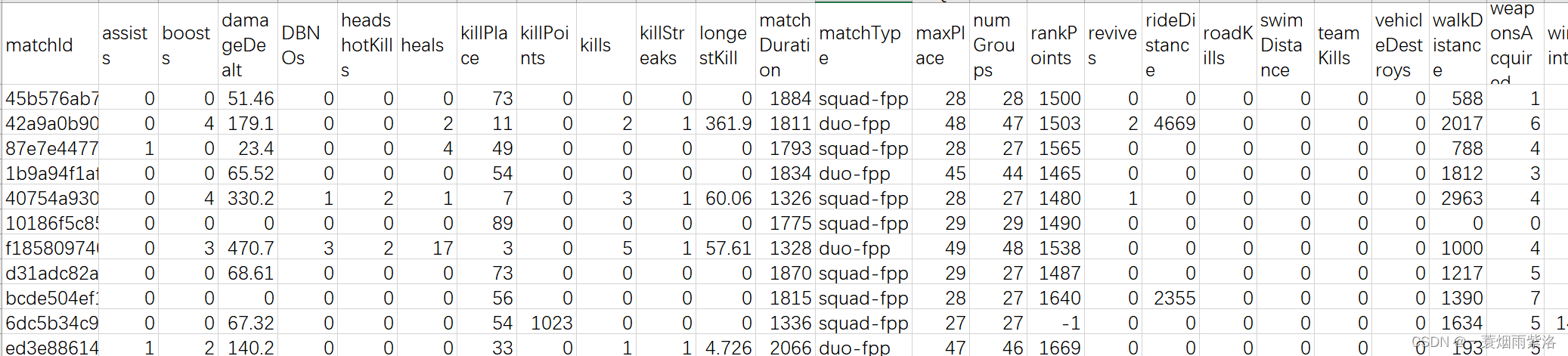
在这里插入图片描述

5.3、项目评估方式

最后结果通过平均绝对误差（MAE)进行评估，即通过预测的winPlacePerc 和真实的winPlacePerc之间的平均绝对误差

关于MAE:sklearn.metrics.mean_absolute_error

MAE:mean Absolute Error 平均绝对误差是绝对误差的平均值
$MAE(x,h)=1/m\sum_1^m|h(x^i-y^i|$

5.4、代码实现

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

train=pd.read_csv("D:/data/data/train_V2.csv")
train.head()
train.tail()
train.describe()
train.info()
train.shape

#有多少场比赛
np.unique(train["matchId"]).shape
#有多少支队伍
np.unique(train["groupId"]).shape

#数据基本处理
#是否有缺失值
np.any(train.isnull())
train[train["winPlacePerc"].isnull()]
#删除
train.drop(2744604)

#特征数据规范化处理
count=train.groupby('matchId')['matchId'].transform('count')
train['playersJoined']=count
count.count()
train.head()

#通过每场参加人数进行，按值升序排列
train["playersJoined"].sort_values().head()

#通过结果发现，最少一局，只有两个人

#通过绘制图像，查看每局开始人生
#通过seaborn下的countplot方法，绘制统计过数量之后的直方图
plt.figure(figsize=(20,10))
sns.countplot(train['playersJoined'])
plt.title('playersJoined')
plt.grid()
plt.show()

plt.figure(figsize=(20,8))
sns.countplot(train[train["playersJoined"]>=75]["playersJoined"])
plt.grid()
plt.show()

#对部分特征值进行规范化
# 可以试想，一局只有70个玩家和一局有100个玩家的杀敌数，一共是不可以同时比较的
#可以考虑特征值1、kill  2、damageDealt   3、maxPlace   4、matchDuration
train["killsNorm"] = train["kills"] * ((100-train["playersJoined"])/100+1)
train["damageDealtNorm"] = train["damageDealt"] * ((100-train["playersJoined"])/100+1)
train["maxPlaceNorm"] = train["maxPlace"] * ((100-train["playersJoined"])/100+1)
train["matchDurationNorm"] = train["matchDuration"] * ((100-train["playersJoined"])/100+1)

#比较经过规范化的特征值和原始特征值的值
to_show = ['Id', 'kills','killsNorm','damageDealt', 'damageDealtNorm', 'maxPlace', 'maxPlaceNorm', 'matchDuration', 'matchDurationNorm']
train[to_show][0:11]

#部分变量合成
train["healsandboosts"]=train["heals"]+train["boosts"]
train[["heals","boosts","healsandboosts"]].tail(20)

#异常值处理
#反常规数据：删除有击杀，但是完全没有移动的玩家
train["totalDistance"]=train["rideDistance"]+train["walkDistance"]+train["swimDistance"]
train.head()

train["killwithoutMoving"] = (train["kills"]>0) &(train["totalDistance"] ==0)
train[train["killwithoutMoving"] == True]

train[train["killwithoutMoving"] == True].shape

train[train["killwithoutMoving"] == True].index

train.drop(train[train["killwithoutMoving"] == True].index,inplace=True)
train.shape

#查看载具杀敌数超过十个的玩家
train[train['roadKills']>10]
#删除这些数据
train.drop(train[train['roadKills']>10].index,inplace=True)
train.shape

#删除玩家在一局杀敌数超过30人的数据
train[train['kills']>30]
#删除这些数据
train.drop(train[train['kills']>30].index,inplace=True)
train.shape

#删除爆头率
train["headshot_rate"] = train["headshotKills"]/train["kills"]
train["headshot_rate"] =train["headshot_rate"].fillna(0)
train.head()
#删除这些数据
train.drop(train[(train["headshot_rate"] ==1) & (train['kills']>9)].index,inplace=True)
train.shape

#删除最远杀敌距离大于等于1KM的玩家
train.drop(train[train["longestKill"]>=1000].index,inplace=True)
train.shape

#删除运动距离异常值
train[train["walkDistance"]>=10000].index
train.drop(train[train["walkDistance"]>=10000].index,inplace=True)
train.shape

train[train["rideDistance"]>=20000].index
train.drop(train[train["rideDistance"]>=20000].index,inplace=True)
train.shape

train[train["swimDistance"]>=2000].index
train.drop(train[train["swimDistance"]>=2000].index,inplace=True)
train.shape

#武器收集异常值处理
train[train["weaponsAcquired"]>=80].index
train.drop(train[train["weaponsAcquired"]>=80].index,inplace=True)
train.shape

#使用药品数量异常
train[train["heals"]>=80].index
train.drop(train[train["heals"]>=80].index,inplace=True)
train.shape


#类别型数据处理
#比赛类型one-hot处理
train["matchType"].unique()
train = pd.get_dummies(train,columns=["matchType"])
train.head()

matchType_encoding = train.filter(regex="matchType")
matchType_encoding.head()

#对groupId,matchId等数据进行处理
train["groupId"].head()
train["groupId"] = train["groupId"].astype("category")
train["groupId_cat"] = train["groupId"].cat.codes
train["groupId_cat"].head()
train.head()

train["matchId"] = train["matchId"].astype("category")
train["matchId_cat"] = train["matchId"].cat.codes
train["matchId_cat"].head()

train.head()

train.drop(["groupId","matchId"], axis=1,inplace=True)

#数据截取、、分割数据集
df_sample=train.sample(100000)
df_sample.shape

#确定特征值和目标值
df = df_sample.drop(["winPlacePerc", "Id"], axis=1)
y=df_sample["winPlacePerc"]

df.shape
y.shape

#分割训练集和测试集
from sklearn.model_selection import train_test_split
x_train,x_valid,y_train,y_valid = train_test_split(df,y,test_size=0.2)
x_train.shape

#机器学习（模型训练）和评估
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error

#使用随机森林进行训练
m1=RandomForestRegressor(n_estimators=40,min_samples_leaf=3,max_features='sqrt',n_jobs=-1)
m1.fit(x_train,y_train)
y_pre=m1.predict(x_valid)
m1.score(x_valid,y_valid)

mean_absolute_error(y_valid,y_pre)
m1.feature_importances_
imp_df=pd.DataFrame({"cols":df.columns,"imp":m1.feature_importances_})
imp_df.head()

imp_df=imp_df.sort_values("imp",ascending=False)
imp_df.head()

imp_df.plot("cols","imp",figsize=(20,8),kind="barh")

to_keep = imp_df[imp_df.imp>0.005].cols
to_keep.shape
df_keep = df(to_keep)
x_train,x_valid,y_train,y_valid=train_test_split(df_keep,y,random_state=0.2)

m2=RandomForestRegressor(n_estimators=40,min_samples_leaf=3,max_features='sqrt',n_jobs=-1)
m2.fit(x_train,y_train)
y_pre=m2.predict(x_valid)
m2.score(x_valid,y_valid)

#使用lightGBM进行模型训练
x_train,x_valid,y_train,y_valid = train_test_split(df,y,test_size=0.2)

import lightgbm as lgb
gbm=lgb.LGBMRegressor(objective="regression",num_leaves=31,learning_rate=0.05,n_estimators=20)
gbm.fit(x_train,y_train,eval_set=[[x_valid,y_valid]],eval_metric="l1",early_stopping_rounds=5)
y_pre=gbm.predict(x_valid)
mean_absolute_error(y_valid,y_pre)



#模型二次调优
from sklearn.model_selection import GridSearchCV
estimator = lgb.LGBMRegressor(num_leaves=31)
param_grid ={
    "learning_rate":[0.01,0.1,1],
    "n_estimators":[40,60,80,100,200,300]
}
gbm=GridSearchCV(estimator,param_grid,cv=5,n_jobs=-1)
gbm.fit(x_train,y_train)
y_pre=gbm.predict(x_valid)
mean_absolute_error(y_valid,y_pre)
gbm.best_params_
#print('交叉验证\网格搜索最好的参数',gbm.best_params_)

#模型三次调优
score = []
n_estimators = [100,500,1000]
for nes in n_estimators:
    lgbm = lgb.LGBMRegressor(boosting_type='gbdt',
                             num_leaves=31,
                             max_depth=5,
                             learning_rate=0.1,
                             n_estimators=nes,
                             min_child_samples=20,
                             n_jobs=-1)
    lgbm.fit(x_train, y_train,eval_set=[(x_valid,y_valid)],eval_metric="l1",early_stopping_rounds=5)
    y_pre = lgbm.predict(x_valid)
    mea=mean_absolute_error(y_valid, y_pre)
    score.append(mea)
    print("test data mea eval :{}".format(mea))

plt.plot(n_estimators,score,'o-')
plt.ylabel("mea")
plt.xlabel("n_estimator")
print("best n_estimator {}".format(n_estimators[np.argmin(score)]))

原文链接：https://blog.csdn.net/weixin_34280060/article/details/123635528