一、向量的加减,点乘叉乘(略)
二、典型坐标系: (笛卡尔,圆柱,球)
1.笛卡尔坐标(最常见,向量为三个方向的偏移量)
2.圆柱坐标系(Cylindrical coordinate)
标记为, 简记为带有高度的极坐标系
3.球坐标系(Spherical coordiante)
标记为,几何意义:原点与点P之间的“径向距离”(radial distance)r,原点到点P的连线与正z-轴之间的“极角”(polar angle)
,以及原点到点P的连线在xy-平面的投影线,与正x-轴之间的“方位角”(azimuth angle)
三、梯度,散度和旋度
nabla算符():为方便记忆,先提出nabla算符的概念。
nabla算符表示为: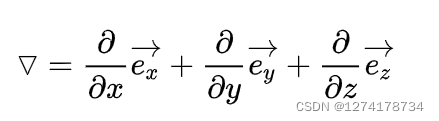
本身没有意义,和函数作用之后即可用于计算梯度,散度和旋度
1、梯度和方向向量(Gradient)
粗略理解:把山脉放在坐标轴里面,方向向量就是沿某点自由下降的反方向,梯度表示的就是使得下降速度最快的方向和值。
计算:对于u(x,y,z):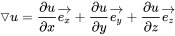
2、散度(Divergence)
粗略理解:一个场里面分子舒张或收缩的速度(标量,无方向有正负,发散的方向为正
计算:
在圆柱/球坐标系中:

举例:

f为一个三元函数,运用nabla算符与f点乘(主要为方便记忆,并非实际运算过程)得出散度的结果
3、旋度(Crul)
粗略理解:物体在场中趋向于旋转的方向和大小,逆时针为正,顺时针为负
计算:(将nabla和向量叉乘)
举例:
(要记住叉积的过程)
四、主要性质
1.梯度的旋度永远为0

2. 由于标量的梯度为矢量,因此可以继续对梯度求散度,引入拉普拉斯算子:
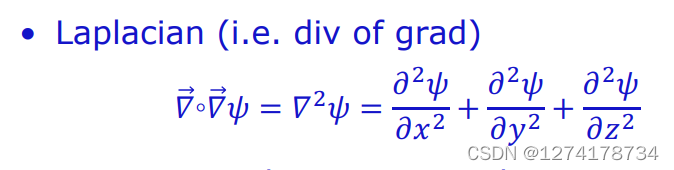
3.散度的梯度减去梯度的散度等于旋度的旋度
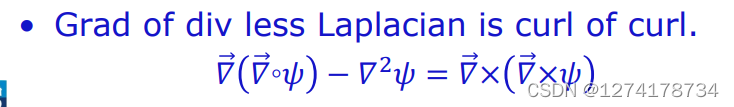
4.对于任意足够光滑、快速衰减的向量场可分解为一个无旋向量场和一个螺线向量场的和(亥姆霍兹分解)
5.如果一个场的旋度处处为0,则该场可以被写为一个标量势的梯度
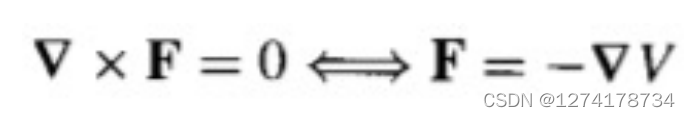
6.电场力做功可以用积分形式表示(略)