机器学习（Coursera吴恩达）（二）

标签（空格分隔）： 机器学习

多变量线性回归(Linear Regression with Multiple Variables)

多维特性

构建一个有n个变量的模型，模型中的特征为($x_1,x_2,x_3,...,x_n$)。例如房价预测问题，除了房子面积之外还可以加如房间数，楼层位置，新旧程度等很多相关的特征，这样就构建了一个多变量模型。

• n表示特征数量。
• $x^{(i)}$表示第i个样本实例，是一个向量，包含这个样本所对应的所有特征。例如$x^{(2)}=[1416,3,2,40]^T$
• ${x}_{j}^{(i)}$表示第i个样本实例的第j个特征。$x^{(2)}_{2}=3$
• 多变量的假设线性函数为：$h_\theta(x)=\theta_0+\theta_1x1+\theta_2x_2+...+\theta_nx_n$因为有n个特征$\theta$向量就有n+1维（包含一个$\theta_0$）。
• 因为$\theta\in {\mathbb{R}}^{n+1}$，而x是n维的，所以需要给样本$x$添加一个$x_0=1$项，使$x \in \mathbb{R}^{n+1}$。保持维度一致。也就是改为$\theta_0x_0$。$h_\theta(x)=\theta^Tx$

这个模型目的是求$\theta$参数，使代价函数最小。

梯度下降

cost function: $J(\theta_0,\theta_1,...\theta_n)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$
目的：求出是的代价函数最小的一系列参数$\theta$

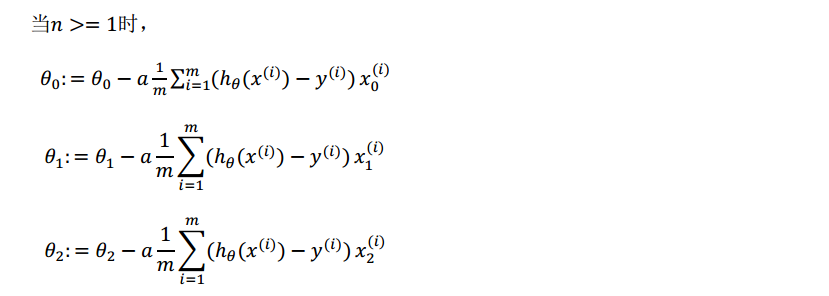
在初始化之后，进行这样的学习循环，直到收敛。

#这个地方有问题，X*theta.T所以X是怎么保存样本的。
#theta是1*n，theta.T是n*1，X是m*n的，也就是样本矩阵每一行保存一个样本，每一列是对应的特征数。
def computeCost(X, y, theta):
    inner = np.power(((X*theta.T)-y, 2)
    return np.sum(inner)/(2.len(X))

特征缩放

梯度下降法需要多次迭代才能收敛。如果按照原始的特征绘制代价函数等高线，则是一个椭圆的，显得很扁。而且梯度下降方向是曲折的。为了解决这个问题，并且加快梯度下降，就需要进行特征缩放，将特征尺度缩放到[-1，1]之间。这样等高线图类似一个圆，可以加快下降。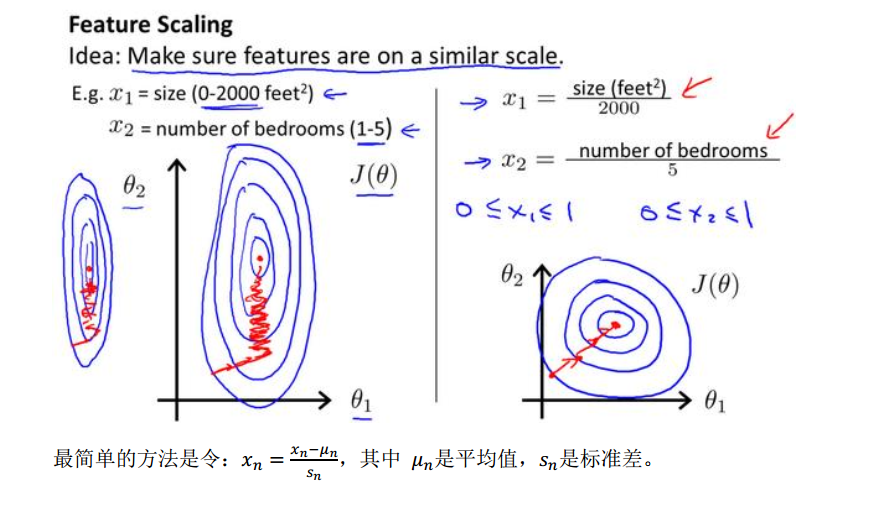

特征缩放没有一个特别的区间，只要合适就可以。

学习率

学习率控制下降的步长，$\alpha$过小则达到收敛所需的迭代次数会很高；如果过大，则迭代可能不会减小代价函数。可能越过极小点，导致无法收敛。

通常可以尝试0.1 0.3 0.01 0.03 1 3这些量。

正规方程

正规方程是求解下面的方程来找出代价函数最小的参数。
假设训练集特征矩阵为X(包含$x_0$)，并且训练集结果为向量y，则利用正规方程解出向量$\theta=(X^TX)^{-1}X^Ty$。

正规方程是求解某些线性问题回归的方法。
下面的对比很重要，矩阵求逆计算复杂度较高$O(n^3)$。

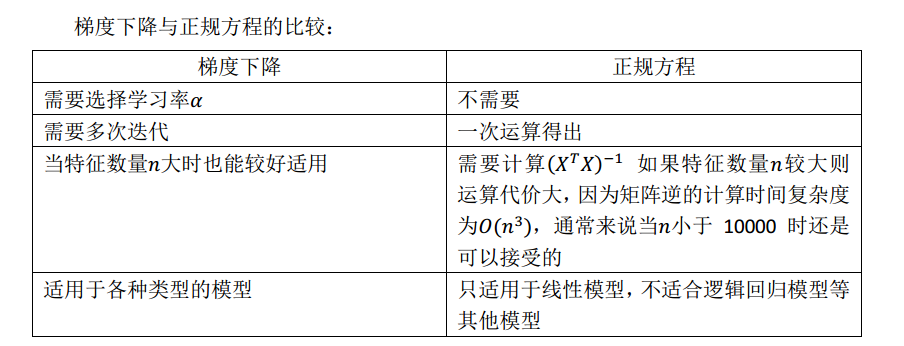
import numpy as np
def normalEqn(X,y)
    return np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)

正规方程有可能是不可逆的，如果来展示两个相关联的特征的话，那么X’X是不可逆的。
在MATLAB中可以用pinv()进行伪逆计算，得到一个可用的值，但实际并不可逆。

正规方程的推到过程是矩阵的求导：

。。。待定上传一张图片。。。