自动控制原理＜四＞

五、PI控制器

我们还是先来看看第三节课中所说的一阶系统中仅仅使用比例调节会产生稳态误差，如下

• Kp<-1时：极点位于右半平面，系统不稳定，也谈不上稳态误差一说。

• Kp>-1时：极点位于左半平面，系统稳定，存在稳定误差r/(1+Kp)。

综上所述，我们怎么去分析一个简单的系统呢？

​ ①分析极点所处的位置

​ ②若系统稳定，分析系统的误差

到目前为止是这样去分析就够了，后面再深入，接下来我们深入分析怎么减小稳态误差。

想要减小稳态误差，那么我们就必须对控制器进行新的改造设计，我们将一阶系统中所有的Kp替换为C(s),C(s)就是我们新设计的控制器，假设系统是稳定的，如下图所示：

设计新的控制器的标准，使用终止定理的最终输出值=输入的参考值。

要想s->0时，C(s)趋于无穷大，可想C(s)必须是一个反比例函数。

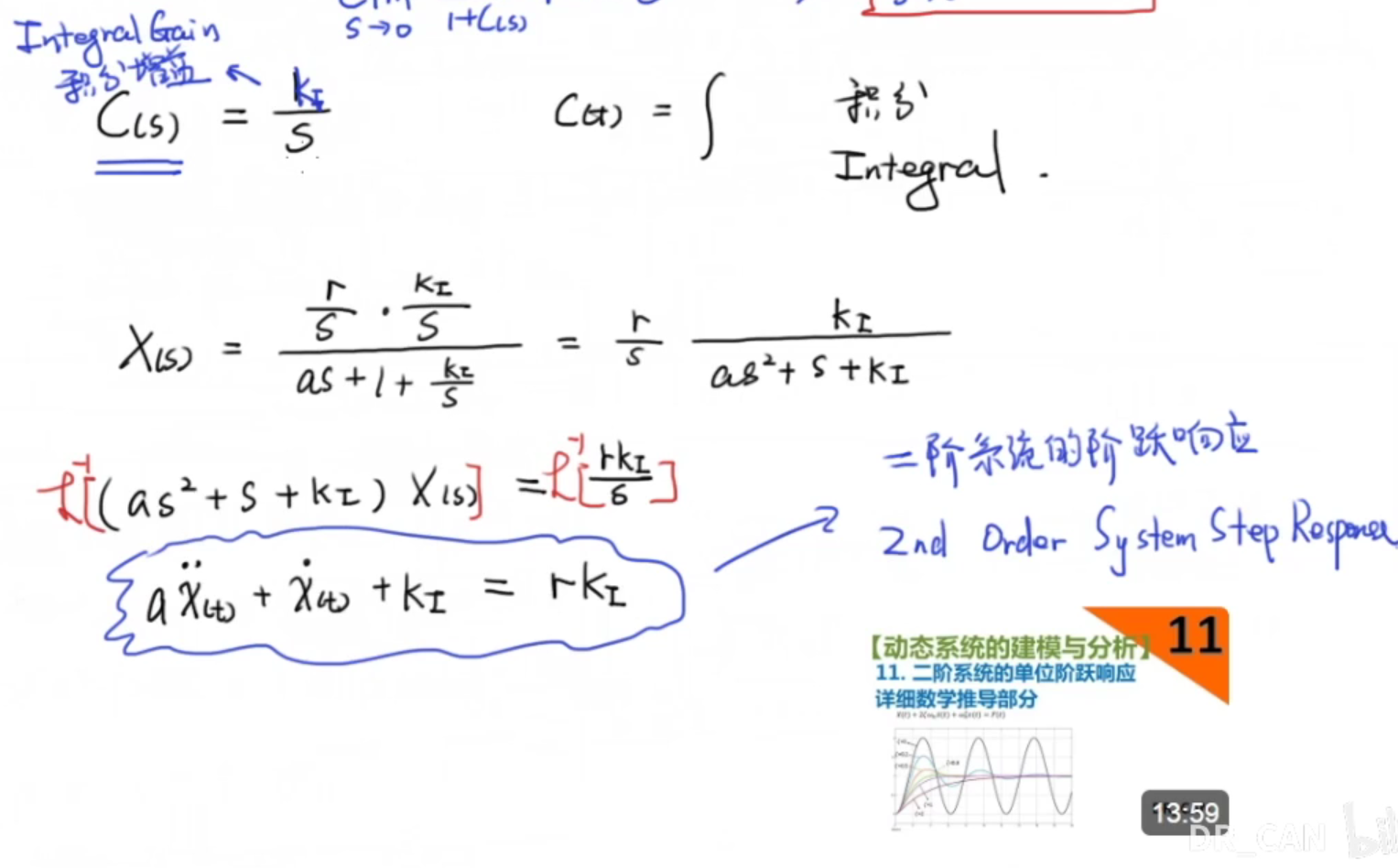
所以最终可得C(s) = 1/s，在时域中这就是微分。

我们将新的控制器C(s)加入原有的传递函数中，使用拉普拉斯反变换对其时域再进行分析，可以发现原有的一阶方程，变成了二阶方程，这将导致微分控制系统中会产生振荡。

我们来看看比例和微分控制器之间的区别，设定参考值为1

• 灰色：微分控制器
• 蓝色：比例控制器

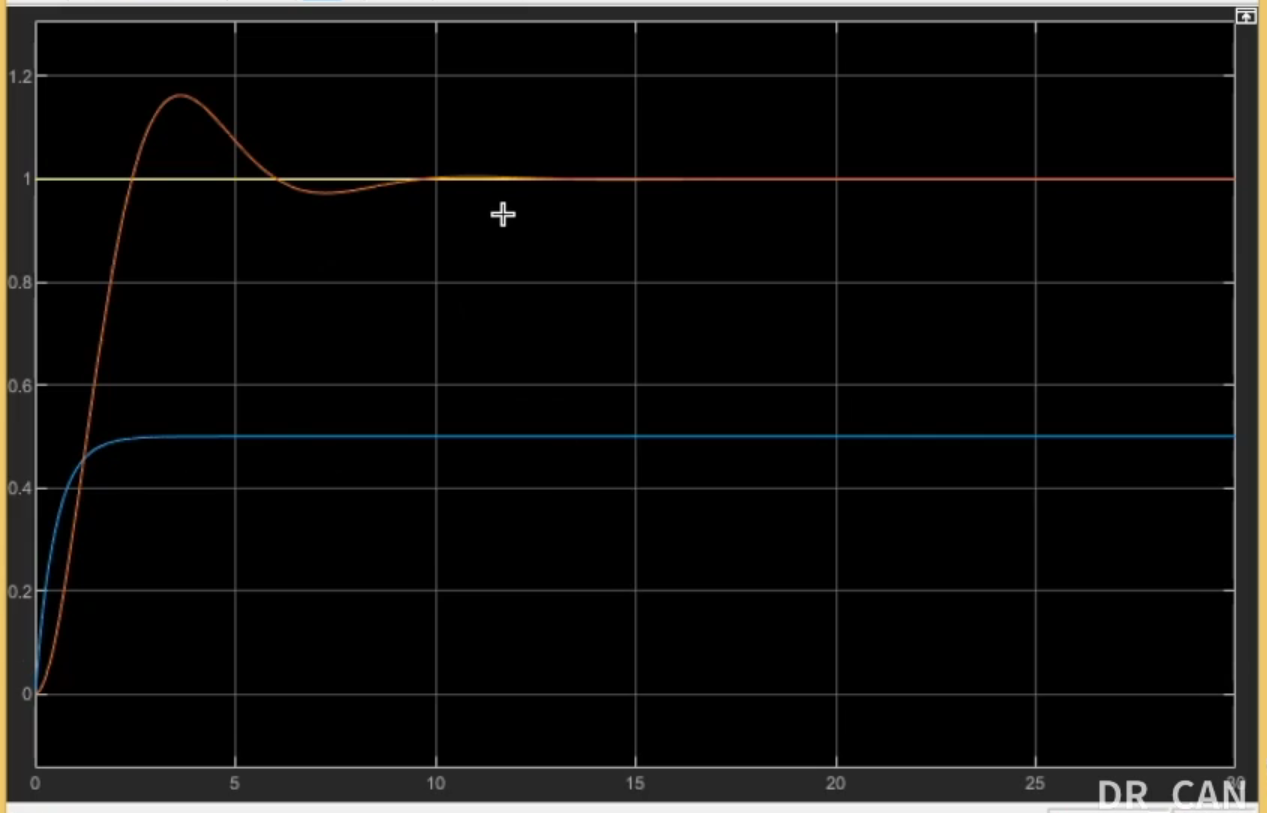
在比例控制器中存在明显的静态误差，1-0.5 = 0.5 ，大概为0.5左右

在微分控制器中消除了稳态误差，但是引入了低频振荡，那么该怎么办呢？且相应速度没有仅仅使用比例调节的快，下面我们再进行进一步的实验。

我们再来看看比例和微分控制器共同作用的效果，设定参考值为1

• 灰色：微分控制器
• 蓝色：比例控制器
• 绿色：比例-微分控制器

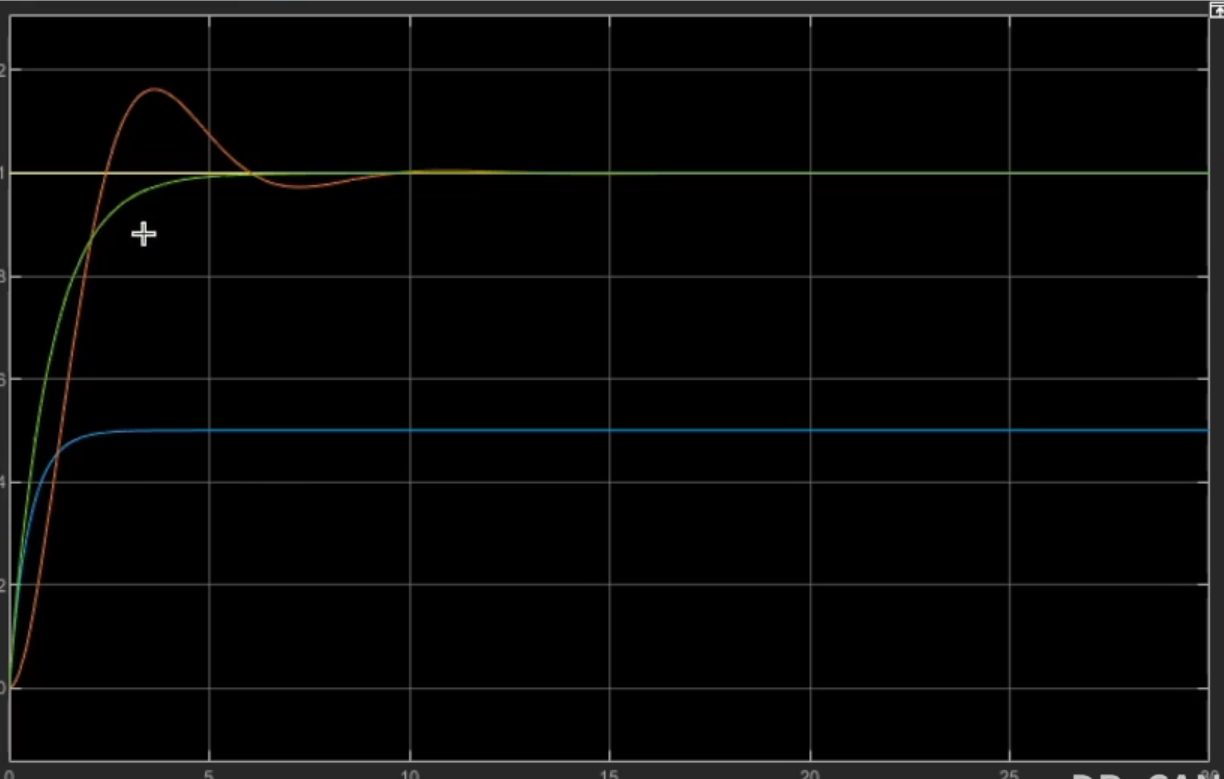
明显的消除了低频抖动，也加快了相应，所以有的时候使用PI控制器，往往可以达到良好的控制效果。在两轮平衡小车中的速度环使用的就是PI控制器。