GNSS速度场简易MATLAB克里金插值

引言

由于GPS观测点分布离散且不均匀，在进行应变计算和分析前，需要对速度场进行插值，获得均匀分布的速度场。一般采用Kriging 法估计在均匀网格节点上的速度值，需要下载克里金MATLAB工具箱（matlab_Kriging_toolbox）并添加到路径中 （下载链接：https://pan.baidu.com/s/1p0lt2G8KQ-els7Dyw5jPFg，提取码：wcss）

克里金插值原理

网上介绍克里金插值的帖子和文章非常多，这里推荐几个供大家参考：

• 对理解公式原理非常有帮助的：
  https://xg1990.com/blog/archives/222
  https://zhuanlan.zhihu.com/p/89619040

• 比较详细介绍Dace中例子的文章：https://blog.csdn.net/qq_40937675/article/details/89792122
  

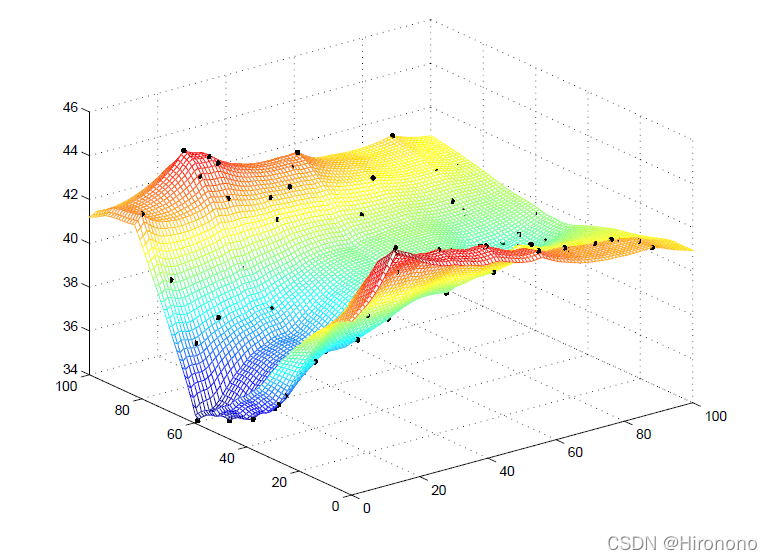
克里金插值步骤

• (1)对于观测数据，两两计算距离与半方差
• (2)寻找一个拟合曲线拟合距离与半方差的关系，从而能根据任意距离计算出相应的半方差
• (3)计算出所有已知点之间的半方差 rij
• (4)对于未知点 zo，计算它到所有已知点 zi的半方差 rio
• (5)求解第四节中的方程组，得到最优系数 λi 使用最优系数
• (6)对已知点的属性值进行加权求和，得到未知点 zo的估计值

实例阐述

在具体用matlab实现时分为以下几步：

• 1）导入观测数据文件，包含点位坐标和观测值，建立变量。
  在GNSS观测值中包含北东高三个方向的形变量，由于GNSS观测对于垂直向形变不敏感，因此在插值的时候是使用了水平两个方向的形变量。
• 2）设置范围和格网大小使用工具箱进行插值。
• 3）根据点位误差大小调整拟合函数及其他参数。
  Dace工具箱中对于回归函数包含0阶、1阶和2阶多项式三种，对于相关函数包含指数函数、高斯函数、线性函数、球谐函数等六种，每种函数的拟合效果不同，可以根据实际的数据拟合情况来酌情选择合适的函数。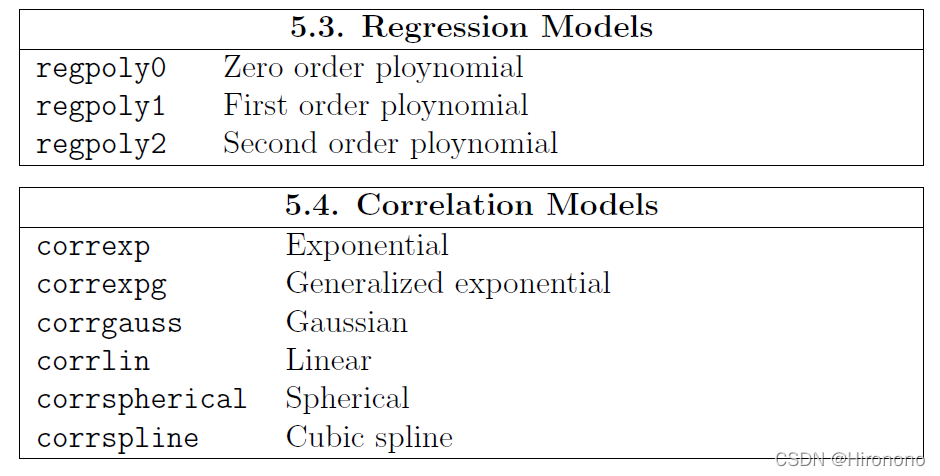
  
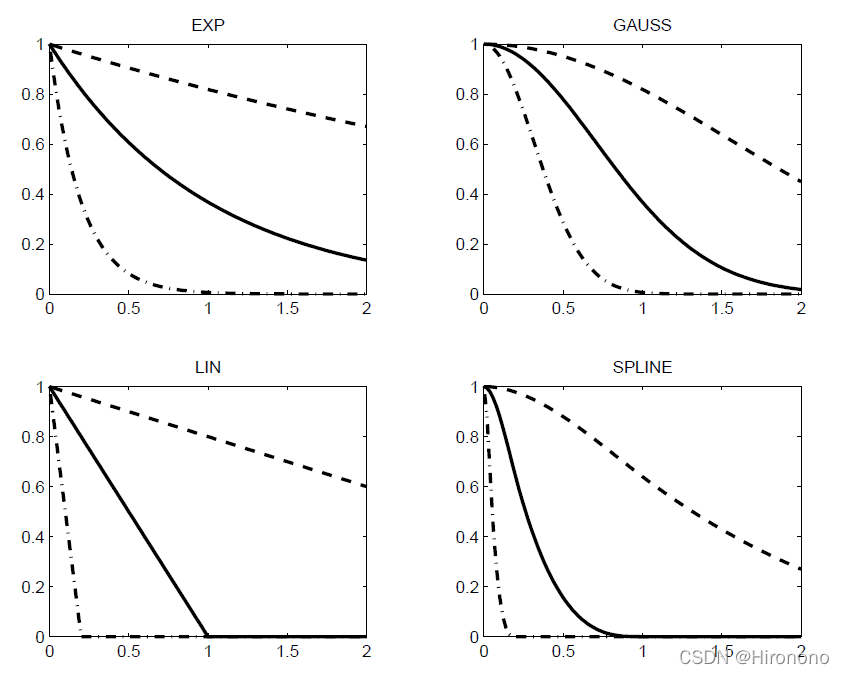
• 4）输出插值点文件并进行可视化，为便于绘制各点的误差圆，我是输出文件后在GMT中进行可视化。

附件代码如下，可先尝试Dace工具箱中的例子，之后按照其例子修改：

%% 导入文件，切出各列
GPS_file=xlsread('GPSdata.xlsx');
lon=GPS_file(:,1);
lat=GPS_file(:,2);
v_e=GPS_file(:,3);
v_n=GPS_file(:,4);
v_h=sqrt(v_e.*v_e+v_n.*v_n);
sigma_e=GPS_file(:,5);
sigma_n=GPS_file(:,6);

%% GPS速度插值  克里希金插值法
% 下载克里希金工具箱并添加到路径中 matlab_Kriging_toolbox
% https://pan.baidu.com/s/1p0lt2G8KQ-els7Dyw5jPFg?errmsg=Auth+Login+Params+Not+Corret&errno=2&ssnerror=0
%S存储了点位坐标值，Y为观测值 (分为两次预测e n)
S=GPS_file(:,1:2);
E=GPS_file(:,3);
N=GPS_file(:,4);
%模型参数设置，无特殊情况不需修改，详见安装包中PDF说明书
theta = [0.1]; lob = [1e-1]; upb = [100];
%变异函数模型为指数函数模型，这里@的参数可以设置不同的函数，详见手册
[dmodel_N, perf_N] = dacefit(S, N, @regpoly2, @correxp, theta, lob, upb);
[dmodel_E, perf_E] = dacefit(S, E, @regpoly2, @correxp, theta, lob, upb);

%创建格网
scale=25; %格网大小
X = gridsamp([88 44;112 55], scale);    % 在整个范围内划分出scale*scale的网格 X是可以通用的

% X=[83.731	32.36];     %单点预测的实现
%格网点的预测值返回在矩阵YX中，预测点的均方根误差返回在矩阵MSE中
[YX_E,MSE_E] = predictor(X, dmodel_E); 
[YX_N,MSE_N] = predictor(X, dmodel_N);    
X1 = reshape(X(:,1),scale,scale); X2 = reshape(X(:,2),scale,scale);
YX_E = reshape(YX_E, size(X1));         %size(X1)=40*40
YX_N = reshape(YX_N, size(X1));         %size(X1)=40*40
figure; 
mesh(X1, X2, YX_E)         %绘制预测表面
hold on,
plot3(S(:,1),S(:,2),E,'.k', 'MarkerSize',10)    %绘制原始散点数据
xlabel('Longitude(degree)');
ylabel('Latitude(degree)');
zlabel('V_E');
colorbar;
% imagesc
xlim([88,112]);
hold off
figure;
mesh(X1, X2, reshape(MSE_E,size(X1)));  %绘制每个点的插值误差大小
xlim([88,112]);
title('MSE for each point');

% 将插值后的E N、经纬度及单点误差输出到文件grd/dat，可直接用于GMT画图
% grdwrite2(X1,X2',YX_E','VE_afterinterp.grd');
% Path_Out = strcat('.\','Outfiles', '\','station_afterinterp','\');
fname=strcat('VELO_afterinterp_15.out');
fid = fopen(fname,'w');
m=scale*scale;
X1_1 = reshape(X1,m,1);
X2_1 = reshape(X2,m,1);
YX_E1 = reshape(YX_E,m,1);
YX_N1 = reshape(YX_N,m,1);
    for i=1:m
        fprintf(fid,'%f\t%f\t%f\t%f\t%f\t%f\n',X1_1(i,1),X2_1(i,1),YX_E1(i,1),YX_N1(i,1),MSE_E(i,1),MSE_N(i,1));
    end
fclose(fid);